
- •§1. Эллипс
- •2. Исследование формы эллипса по его уравнению
- •3.Эксцентриситет эллипса
- •4.Параметрические уравнения эллипса
- •5.Построение точек эллипса
- •§2 Гипербола
- •1. Определение гиперболы и её уравнение
- •2. Исследование формы гиперболы по её уравнению
- •3.Эксцентриситет гиперболы
- •5.Построение точек гиперболы
- •§3. Парабола
- •1. Определение параболы и её уравнение
- •2. Исследование формы параболы по его уравнению
- •3.Построение точек параболы
- •§4.Решение задач
3.Эксцентриситет гиперболы
Рассмотрим гиперболу с фокусами в точках F1 и F2 , действительной осью которой является [A1A2].
Определение. Эксцентриситетом гиперболы называется число, равное .
Так как
![]() ,
то ε > 1.
Пусть гипербола задана уравнением
,
то ε > 1.
Пусть гипербола задана уравнением
![]() ,
тогда
,
тогда
![]() =>
=>
![]() =>
=>
![]() .
=> Эксцентриситет определяется
отношением полуосей гиперболы. Чем
меньше эксцентриситет гиперболы, тем
меньше углы, образуемые асимптотами, в
которых лежит гипербола и тем больше
гипербола «вытягивается» вдоль своей
действительной оси. Рис.10
.
=> Эксцентриситет определяется
отношением полуосей гиперболы. Чем
меньше эксцентриситет гиперболы, тем
меньше углы, образуемые асимптотами, в
которых лежит гипербола и тем больше
гипербола «вытягивается» вдоль своей
действительной оси. Рис.10
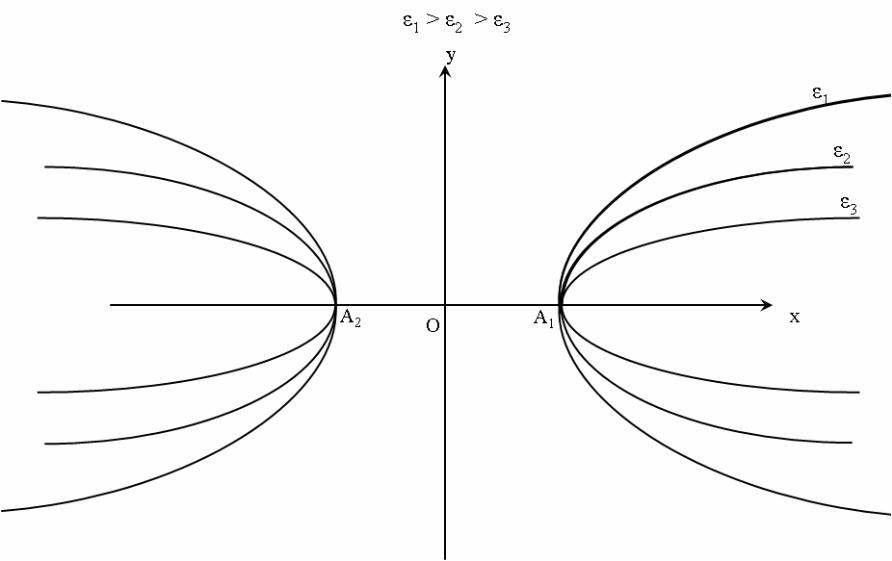
Рис.10.
5.Построение точек гиперболы
Если для гиперболы заданы положения её вершин A1 , A2 и фокусов F1, F2, то её можно построить следующим образом:
а) Строим окружность ω1(F1,R1) с центром в правом фокусе F1 произвольным радиусом R1.
б) Строим окружность ω2(F2,R2) с центром в левом фокусе F2 радиусом R2 = R1+[A1A2].
в) В этом случае точка М =ω1 ∩ ω2 принадлежит гиперболе, так как для этой точки ||F1M| ─|F2M|| = |A1A2| =2a.
Повторяя, построения а), б) и в) несколько раз можно получить необходимое число точек для построения правой ветви гиперболы.

Рис.11.
Левую ветвь гиперболы можно построить аналогично, поменяв фокусы F1 и F2 местами.
Лекция №2
§3. Парабола
1. Определение параболы и её уравнение
Определение. Параболой называется множество всех точек плоскости, для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой d, не проходящей через данную точку F.
Точка F называется фокусом
параболы, а прямая d ─
директрисой параболы. Расстояние от
фокуса до директрисы называется фокальным
параметром параболы и обозначается:
![]() .
.

Рис.12.
Для того чтобы составить уравнение
параболы на плоскости введём
ортонормированную систему координат,
ось (Ох) которой выберем проходящей
через фокус F параболы
перпендикулярно директрисе d.
Пусть D─ точка пересечения
оси (Ох) с директрисой d.
Начало системы координат выберем в
точке, являющейся серединой отрезка
[FD]. (
F1 M
|
Таим образом, получаем, если точка М(х;у) принадлежит параболе, то её координаты удовлетворяют уравнению .
Покажем теперь, что если координаты некоторой точки М1(х1;у1) удовлетворяют уравнению (7), то точка М1 принадлежит параболе.
И так, пусть для координат точки М1
выполнено условие:
.
Вычислим
![]()
![]() .
=>
.
=>
![]() => =>
=> =>
![]() параболе. Таким образом, уравнение (7)
является уравнением параболы.
параболе. Таким образом, уравнение (7)
является уравнением параболы.
