
- •§1. Эллипс
- •2. Исследование формы эллипса по его уравнению
- •3.Эксцентриситет эллипса
- •4.Параметрические уравнения эллипса
- •5.Построение точек эллипса
- •§2 Гипербола
- •1. Определение гиперболы и её уравнение
- •2. Исследование формы гиперболы по её уравнению
- •3.Эксцентриситет гиперболы
- •5.Построение точек гиперболы
- •§3. Парабола
- •1. Определение параболы и её уравнение
- •2. Исследование формы параболы по его уравнению
- •3.Построение точек параболы
- •§4.Решение задач
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
УНИВЕРСИТЕТ»
КРИВЫЕ ВТОРОГО ПОРЯДКА
Учебно-методическое пособие
для студентов I курса дневного и заочного отделений
физико-математического факультета
Воронеж 2012
УДК 513 (075.8)
Составитель:
Кандидат физико-математических наук, доцент Н.А. Заварзина
Кривые второго порядка
Лекция №1
§1. Эллипс
1. Определение эллипса и его уравнение
Определение. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскости F1 и F2 есть величина постоянная, равная 2a > ǀF1F2ǀ=2c.
Точки F1 и F2 называются фокусами эллипса, а │F1F2│= 2с ─ фокальным расстоянием.
Пусть на плоскости даны две точки F1 и F2. Для того чтобы составить уравнение эллипса на плоскости введём ортонормированную систему координат, начало которой поместим с середину отрезка [F1F2] . Ось Ох расположим таким образом, чтобы точки F1 и F2 принадлежали этой оси.
F2
F1
M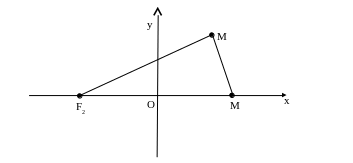




Рис.1.
В этом случае фокусы эллипса принимают следующие координаты F1(c;0) и F2(-c;0). (см. Рис.1.) Пусть М(х;у) ─ произвольная точка эллипса. Тогда, по определению, │МF1│+ │МF2│ = 2a. (1)
По формуле вычисления расстояния между
точками имеем:
![]() ,
,
![]() . Таким образом из (1) =>
. Таким образом из (1) =>
![]() .
Запишем полученное выражение в виде
.
Запишем полученное выражение в виде
![]() и возведём в квадрат. В результате,
после приведения подобных членов,
получаем
и возведём в квадрат. В результате,
после приведения подобных членов,
получаем
![]() .
Для того чтобы освободиться от корня
возведём последнее выражение в квадрат.
В результате после элементарных
преобразований имеем:
.
Для того чтобы освободиться от корня
возведём последнее выражение в квадрат.
В результате после элементарных
преобразований имеем:
![]() .
(2)
.
(2)
|
|
![]() (4)
(4)
Покажем теперь, что если координаты некоторой точки М1(х1;у1) удовлетворяют уравнению (4), то точка М1 принадлежит эллипсу.
Пусть для точки М1(х1;у1)
справедливо равенство
![]() (5)
(5)
Из (5) следует:
 (6)
(6)
Вычислим

![]()
![]() =>
=>
![]() .
.
Заметим, что величина стоящая под
знаком модуля положительна не только
при
![]() <
0, но и при
>
0 так как с <
и из (6) =>
<
0, но и при
>
0 так как с <
и из (6) =>
![]() .
.
Аналогично, если провести подобные
преобразования для
![]() ,
получим
,
получим
![]() .
=>
.
=>
![]() => точка М1 принадлежит эллипсу.
=> точка М1 принадлежит эллипсу.
Таким образом, уравнение (4) является уравнением эллипса, которое называется каноническим уравнением эллипса.
[MF1] ─ называется
первым фокальным радиусом эллипса;
![]() .
.
[MF2] ─ называется
вторым фокальным радиусом эллипса;
![]() .
.
Заметим, что если F1=
F2 , то с = 0 и
![]() =>
=>
![]() => окружность частный случай эллипса.
=> окружность частный случай эллипса.
2. Исследование формы эллипса по его уравнению
Пусть дан эллипс своим каноническим уравнением (4) .
Для определения вида кривой заданной уравнением (4), заметим:
а) Координаты начала системы координат точки О(0;0) не удовлетворяют
уравнению (4). => Эллипс не проходит через начало координат.
б) Найдём точки пересечения эллипса с
осью Ох :
 =>
=>
![]() => Эллипс две точки пересечения с осью
Ох :
=> Эллипс две точки пересечения с осью
Ох :
![]() и
и
![]() .
.
в) Найдём точки пересечения эллипса с
осью Оу :
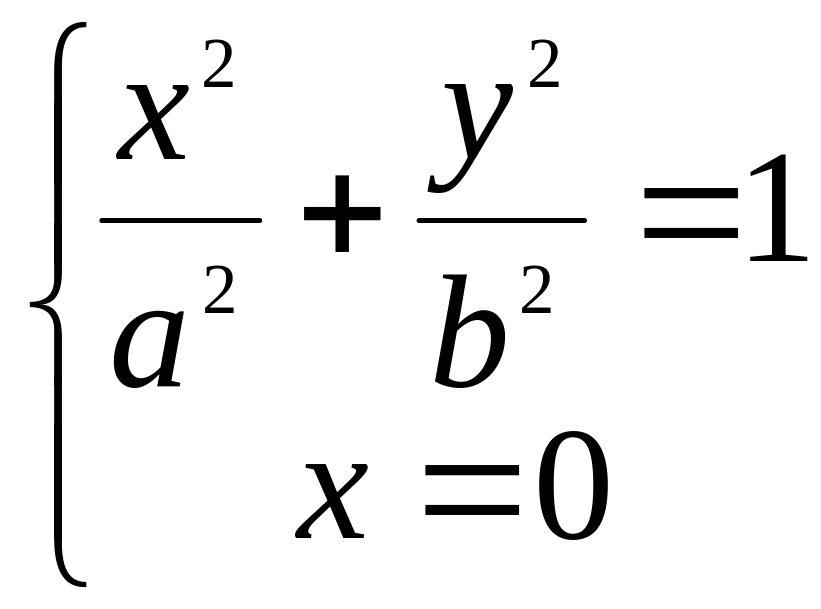 =>
=>
![]() => Эллипс две точки пересечения с осью
Ох :
=> Эллипс две точки пересечения с осью
Ох :
![]() и
и
![]() .
.
г) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М1(-х;у) принадлежит эллипсу. => Эллипс симметричен относительно оси Ох.
д) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М2(х;-у) принадлежит эллипсу. => Эллипс симметричен относительно оси Оу.
На основании г) и д) можно сделать вывод, что эллипс симметричен относительно начала системы координат.
е) Из уравнения (4)
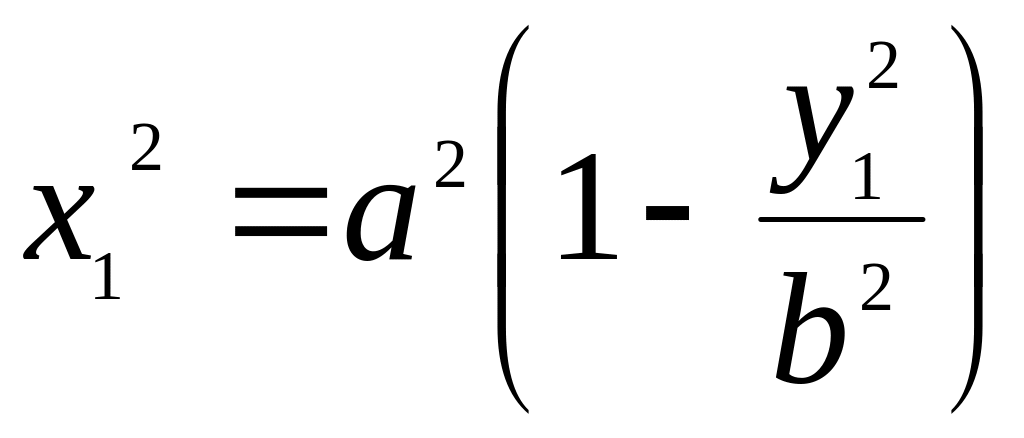 ,
=>
,
=>
![]() и
и
![]() => Все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми
и
.
=> Все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми
и
.
ж) Так как
![]() , то можно сделать вывод, что с ростом
у от 0
, то можно сделать вывод, что с ростом
у от 0
до
![]() величина х убывает от
до 0.
величина х убывает от
до 0.
з)
![]() =>
=>
![]() =>
=>
![]() =>
=>
![]() <0
=> Если
<0
=> Если
![]() ,
то
,
то
![]() ,
то есть функция
,
то есть функция
![]() выпукла вверх. Учитывая симметричность
эллипса относительно осей координат,
получаем изображение эллипса (Рис.2.).
выпукла вверх. Учитывая симметричность
эллипса относительно осей координат,
получаем изображение эллипса (Рис.2.).

Рис.2
Точки А1, А2, В1,
В2 ─ называют вершинами эллипса.
[A1A2]
─ большой осью эллипса, [B1B2]
─ называют малой осью эллипса. Числа
и
![]() называют полуосями эллипса.
называют полуосями эллипса.
