43) Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами.
Линейным
однородным уравнением 
-го
порядка с постоянными коэффициентами
называется уравнение вида
(1)
где
коэффициенты 
–
некоторые действительные числа. Для
нахождения частных решении уравнения
(1) составляют характеристическое
уравнение
(2)
которое получается из уравнения (1) заменой в нем производных искомой функции соответствующими степенями k, причем сама функция заменяется единицей. Уравнение (2) является уравнением n степени и имеет n корней.
Тогда общее решение дифференциального уравнения (1) строится в зависимости от характера корней уравнения (2):
1.каждому
действительному простому корню k в
общем решении соответствует слагаемое
вида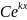 
;
2.каждому
действительному корню кратности 
в
общем решении соответствует
слагаемое вида 
;
3.каждой паре
комплексных сопряженных простых
корней 
и 
в
общем решении соответствует слагаемое
вида 
4.каждой паре
комплексных сопряженных
корней
и 
кратности
в
общем решении соответствует слагаемое
вида
51) Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора.
Ряд Тейлора
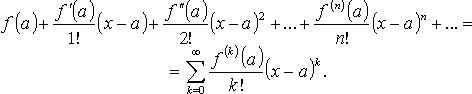
Основные разложения в ряд Тейлора
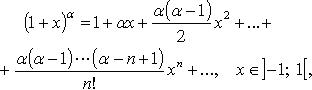
53)
Ряд Лорана —
двусторонне бесконечный степенной ряд
по целым степеням 
,
то есть ряд вида
Этот ряд понимается как сумма двух рядов:
— положительная
часть ряда
Лорана (иногда называется правильной)
и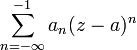
— отрицательная
часть ряда
Лорана (иногда называется главной).
При этом ряд Лорана считается сходящимся тогда и только тогда, когда сходятся его правильная и главная части. Область сходимости ряда по положительным степеням разложения функции в ряд есть сфера радиуса сходимости
.
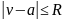В области этой сферы лежит и область
сходимости ряда по изолированному
направлению делителей нуля. Если R=0,
то ряд сходится только в точке a,
если 
,
то ряд сходится во всем пространстве Y.
Ряд по отрицательным степеням
разложения функции сходится в сфере
сходимости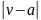
>r.
Если r<R,
то ряд сходится в области заключенной
между двумя концентрическими сферами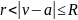 
.
На эту область накладывается область
сходимости рядов по изолированному
направлению. Сферы в пространстве это
прежде всего поверхности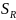 
,
,
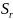
натянутые без точек самопересечения
на пространственные кривые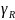 
,
,
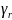эквивалентные кривым типа 
. В
области G,
заключенной между двумя этими сферами,
необходимо рассматривать область
сходимости ряда по изолированному
направлению, для точек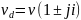 
.
54.Изолированные особые точки аналитических функций: устранимые особые точки; полюсы и их связь с нулями; существенно особые точки.
Точка z=a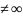
,
в которой функция f(z)
не является аналитической, а в ее
проколотой окрестности аналитическая,
называется изолированной
особой точкой функции f(z).
Такая точка называется устранимой,
если существует
;
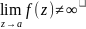полюсом, если
существует
;
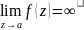и существенно
особой, если
не существует. Характер изолированной
особой точки z=a
функйии f(z)
может быть установлен по виду Лорана
этой функции для кольца
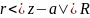следующим образом. Изолированная особая
точка является: 1) устранимой,
если главная часть разложения отсутствует;
2) полюсом,
если главная часть разложения содержит
конечное число членов. При этом, если
главная часть ряда Лорана имеет вид
(
),
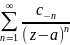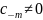число m
называют
порядком полюса z=a
(если m=1,
полюс
называется
простым). В
этом случае функция f(z)
может быть представлена в виде f(z)=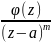
, где
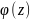– функция, аналитическая в точке z=a
и
;
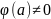3) существенно
особой, если
главная часть разложения содержит
бесконечно число членов, не равных нулю.
Точка z=a
называется нулем
или корнем
кратности m
(или порядка
m)
функции
(аналитической в точке a),
если
,
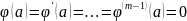но
.
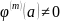Если для аналитической функции
число z=a
есть ноль порядка m,
то для функции f(z)=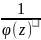
это число является полюсом порядка m.
Отметим, что если f(z)=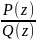
,
где P(z)
и Q(z)
– многочлены, не имеющие общих нулей,
то нули многочлена Q(z),
и только они, являются полюсами функции
f(z),
причем порядок этих полюсов совпадают
с кратностью соответствующих нулей
многочлена Q(z).
Если f(z)
– однозначная аналитическая функция
в области
,
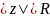понятие особой точки можно распространить
и на бесконечно
удаленную точку z=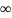
.
Ее тип определяется так же, как для точки
z=a
:
она является устранимой,
если существует
;
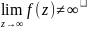полюсом, если
существует
;
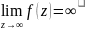и существенно
особой, если
не существует. Рядом
Лорана для
функции f(z)
в окрестности
бесконечно удаленной точки
называется ряд
f(z)=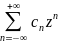
(R
).
Главной частью этого ряда называется часть, состоящая из членов с положительными степенями z, а правильной – часть, содержащая нулевую и отрицательные степени z.