36. Радиус сходимости степенного ряда и его нахождение.

Если степенной ряд (1) сходится не на всей числовой оси, но и не только в точке , то существует число такое, что:

1. ряд абсолютно сходится для ,

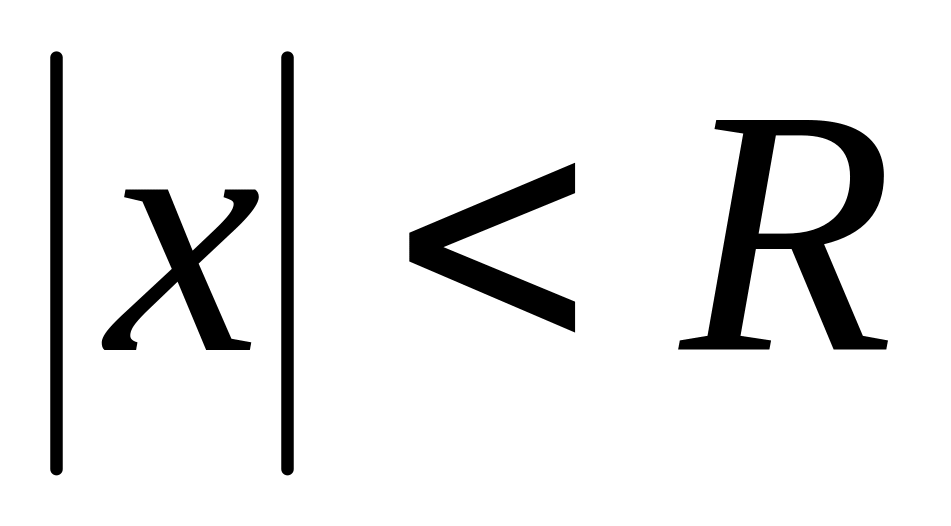2. ряд расходится при .

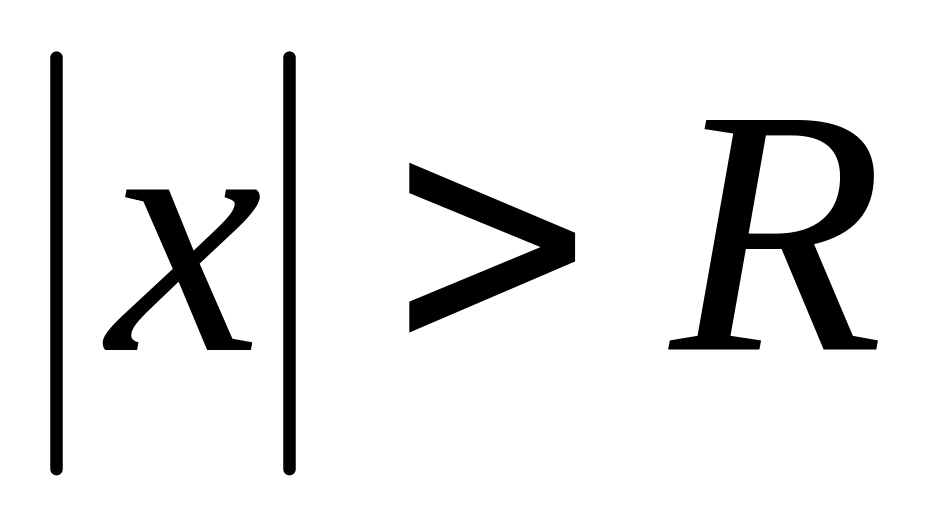Доказательство. По предположению теоремы множество сходимости ряда не пусто и ограничено. Его ограниченность следует из теоремы Абеля, поскольку предполагается, что имеется хотя бы одна точка расходимости ряда (тогда точки расходимости удовлетворяют неравенству , а точки сходимости – ). У ограниченного множества существует точная верхняя грань, которую обозначим . Число обладает тем свойством, что в любой его окрестности есть точки, которые как принадлежат множеству , так и не принадлежат ему. Таким образом, в любой окрестности есть точки, в которых ряд сходится, а так же точки, в которых он расходится. Тогда по теореме Абеля при ряд абсолютно сходится, а при – расходится.

Теорема доказана.

Определение. Число , введённое в теореме, называется радиусом сходимости степенного ряда. Промежуток называется интервалом сходимости степенного ряда.

В упоминавшейся ситуации 1) считают, что (ряд (1) сходится лишь при ); в ситуации 2) полагают . Следовательно, можно считать, что радиус сходимости удовлетворяет неравенствам .

Остался открытым вопрос о сходимости степенного ряда на концах интервала , то есть в точках . Общего ответа о сходимости ряда в этих точках дать нельзя. В этих точках возможны следующие случаи: 1) ряд расходится в обеих точках; 2) ряд сходится в обеих точках (в этом случае область сходимости ряда обращается в замкнутый промежуток ; 3) ряд сходится в одной из точек и расходится в другой. В каждом конкретном примере надо проводить отдельное исследование поведения степенного ряда на концах интервала .

Замечание. Областью сходимости степенного ряда

(2)

будет либо единственная точка , либо вся числовая прямая, либо интервал , к которому могут присоединяться один или оба конца. Это следует из замены переменной и утверждений, сформулированных для ряда (1).

Для отыскания интервала сходимости можно использовать признаки Даламбера или Коши, применённые к ряду, составленному из абсолютных величин членов степенного ряда (1) или (2), т.е. к ряду

или .

37. Понятие о рядах Тейлора и Маклорена.

Ряд вида

(1)

называется рядом Маклорена функции .

Такой ряд можно образовать для любой бесконечно дифференцируемой функции в точке . Этот ряд есть степенной ряд по степеням переменной ; его коэффициенты называют коэффициентами Маклорена.

Ряд вида

(2)

называется рядом Тейлора функции .

Ряд (2) является степенным рядом по степеням двучлена и может быть образован для любой бесконечно дифференцируемой(-если у неё существуют производные любого порядка) функции в точке . Его коэффициенты называются коэффициентами Тейлора.

Ряды (1) и (2) имеют данное название независимо от того, в какой области они сходятся и является ли функция , которая задаёт коэффициенты этих рядов, их суммой.

Ряд (1) является частным случаем ряда (2) ((1) получается из (2) при ). Временно ограничимся изучением ряда (2). Дальнейшие рассуждения относительно ряда (2) читатель должен самостоятельно перенести на ряд (1).

38. Разложение в ряд Маклорена функций e^x, ln(1+x).

1) ;

Докажем формулу . .

1) , , , ..., , … .

2) , , , …, , … .

3) ~ (знак ~ означает формальное разложение функции в ряд Маклорена).

,

т.е. ряд сходится на интервале .

4) Для всех имеем , т.е. все производные в этом интервале ограничены одним и тем же числом . Следовательно, по теореме(Если все производные функции ограничены в промежутке одним и тем же числом , т.е. , то ряд Тейлора этой функции сходится к ней в этом промежутке) ряд сходится к для любых из . В силу произвольности он сходится к на всей числовой оси.

2) ;

Докажем формулу . .

В разложении введём замену , получим

.

Воспользуемся теоремой о почленном интегрировании степенных рядов. Проинтегрируем это равенство почленно от 0 до :

;

,

т.е. при .

Отметим без доказательства, что данное разложение справедливо также для , т.е. .