19. Дайте определения системы линейно зависимых и системы линейно независимых функций. Установить линейную независимость системы функций , , .

Функции y₁(x), y₂(x), ..., y_n(x), определённые на отрезке [a;b], называются линейно зависимыми на [a;b] , если существуют постоянные α₁, α₂, ..., α_n , не равные нулю одновременно и такие, что α₁y₁(x) + α₂y₂(x) + ... + α_ny_n(x) = 0 для всех x из отрезка [a;b].

В противном случае функции y₁(x), y₂(x), ..., y_n(x) называются линейно независимыми.

Линейную зависимость и линейную независимость функций определяют также на (a;b) , (a;b] , [a;b) , на бесконечных промежутках.

Справедливо следующее утверждение.

Функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других на этом отрезке.

20. Установить линейную зависимость системы функций , , 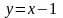. Пусть функции линейно независимы , тогда составим определитель Вронского:

Данные функции линейно зависимы так первую функцию можно представить в виде линейной комбинации двух других 2= 1*(x+1)+(-1)+(x-1), соответственно можно подобрать такие α1,α2,α3 при которых верно равенство: α1*y1+α2*y2+α3*y3=0

1*(x+1)+(-1)*(x-1)+(-1)*2=0

21. Докажите, что сумма частного решения линейного неоднородного дифференциального уравнения второго порядка и общего решения соответствующего однородного уравнения является общим решением линейного неоднородного уравнения второго порядка. Общее решение неоднородного уравнения L(y)=f(x)есть сумма частного решения ‾у(х) этого уравнения и общего решения соответствующего ему однородного уравнения L(y)=0. Доказательство: Покажем сначала, что сумма у(х) частного решения уравнения неоднородного уравнения ‾у(х)и произвольного решения у₀(х) однородного уравнения также является решением неоднородного уравнения. Действительно, в силу леммы имеем L(‾y+y₀)=L(‾y)+L(y₀)=f(x)+0=f(x), что и требовалось доказать. Теперь нам осталось доказать, что всякое решение у(х) неоднородного уравнения есть сумма ‾у(х) и некоторого частного решения у₀(х) уравнения L(y)=f(x). Имеем L(у-‾y)=L(y)-L(‾y)=f(x)-f(x)=0.Следовательно, у₀(х)=у(х)-‾у(х) – решение уравнения L(y)=0, значит, у(х)=у₀(х)+‾у(х), что и завершает доказательство.

Возьмем ур-е (1): . Решением ур-я(1) будет сумма частного и общего решения однородного ур-я .

Док-во. Тогда имеем *: . Возьмем любое решение ур-я (1)**:

Вычтем их ** уравнение *, получим: ЧТД

22. Докажите, что линейная комбинация решений линейного однородного дифференциального уравнения второго порядка также является решением этого уравнения. Пусть у₁(х) и у₂(х),….,у_к(х) – произвольные решения линейного однородного дифференциального уравнения и С₁, С₂,….,С_к – произвольные постоянные, тогда линейная комбинация С₁у₁(х)+С₂у₂(х)+….+С_ку_к(х) также является решением этого уравнения. Действительно, на основании L(C₁y₁+C₂y₂)= C₁L(y₁)+C₂L(y₂), имеем: L(C₁y₁+C₂y₂+….+C_ky_k)=C₁L(y₁)+C₂L(y₂)+…+C_kL(y_k)=0 что и требовалось доказать.

23. Докажите, что общим решением линейного однородного дифференциального уравнения второго порядка является линейная комбинация фундаментальной системы решений этого уравнения.

Пусть у₁(х),……, у_п(х) – фундаментальный набор решений уравнения L(y)=0, тогда общее решение этого уравнения задается формулой: y=C₁y₁+…+C_ny_n. Доказательство. То, что функция у(х), определяемая формулой

С ₁у₁(х₀)+С₂у₂(х₀)+….+С_ку_к(х₀)=0

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_kу’_k(х₀)=0

………………………………………………

С₁у₁^(k-1)(х₀)+С₂у₂^(k-1)(х₀)+…..+ С_kу_k^(k-1)(х₀)=-0

Является решением уравнения L(y)=0, следует из С₁у₁(х)+С₂у₂(х)+….+С_ку_к(х). Покажем теперь что любое решение ѱ (х) уравнения L(y)=0 представимо в виде линейной комбинации функций у₁,…,у_п. Зафиксируем некоторую точку х₀. Введем следующие обозначения ѱ(х₀)=у₀, ѱ’(x₀)=y’₀, …., ѱ^(n-1)(x₀)=y₀^(n-1) рассмотрим систему линейных алгебраических уравнений:

С ₁у₁(х₀)+С₂у₂(х₀)+….+С_nу_n(х₀)=y₀

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_nу’_n(х₀)=y₀

………………………………………………

С₁у₁^(n-1)(х₀)+С₂у₂^(n-1)(х₀)+…..+ С_nу_n^(n-1)(х₀)=y₀^(n-1)

Определителем этой системы является определитель Вронского для функции у₁,…у_п в точке х₀. Ввиду линейной зависимости этих функций данный определитель не равен нулю. Следовательно, у системы

С ₁у₁(х₀)+С₂у₂(х₀)+….+С_nу_n(х₀)=y₀(1.1)

С₁у’₁(х₀)+С₂у’₂(х₀)+…+ С_nу’_n(х₀)=y₀

………………………………………………

С₁у₁^(n-1)(х₀)+С₂у₂^(n-1)(х₀)+…..+ С_nу_n^(n-1)(х₀)=y₀^(n-1)

Существует решение (‾С₁, ‾С₂,….,‾С_п). Тогда функция у(х)=‾С₁у₁(х)+‾С₂у₂(х)+…+‾С_пу_п(х), как это вытекает из (1.1), удовлетворяет тем же начальным условиям. В силу единственности решения задачи Коши имеем ѱ(х)=у(х), т.е. ѱ(х) есть линейная комбинация функции у₁,…у_п. теорема доказана.