
- •Нелинейные системы управления
- •Типовые нелинейности
- •Исследование переходных процессов в нелинейных системах
- •Исследование переходных процессов в нелинейных системах по фазовым портретам
- •Исследование колебательных процессов по фазовым траекториям
- •Метод точечных преобразований
- •Оценка устойчивости колебаний
- •Устойчивость замкнутых нелинейных систем
- •Синтез нелинейных систем
Исследование колебательных процессов по фазовым траекториям
Колебания, возникающие в нелинейных системах, называются автоколебаниями.
В отличие от линейных систем характер колебательных процессов в нелинейных системах может отличаться от гармонического, причем амплитуда колебаний определяется параметрами звеньев, а не начальными условиями, как в линейных системах.
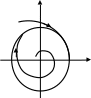
Фазовый портрет, соответствующий автоколебательному процессу, содержит замкнутую траекторию, или так называемый предельный цикл.
 z
z
y
Если все траектории, начинающиеся внутри и снаружи предельного цикла, сходятся к нему, то такой предельный цикл называется устойчивым, и ему будут соответствовать устойчивые автоколебания, причем, если колебания возникают при любых начальных условиях, система называется автоколебательной с мягким возбуждением.
Если же необходимы начальные отклонения у или z больше некоторой величины, то это система с жестким возбуждением.
Системе с жестким возбуждением соответствует фазовый портрет с 2-мя предельными циклами, внутренний – неустойчивый.
 z
z


y
Метод точечных преобразований
Чтобы не строить
полностью фазовую траекторию, поступают
следующим образом: задав начальные
условия, например, при ![]() ,
по уравнению фазовой траектории
определяют координаты в точке следующего
пересечения фазовой траектории с
действительной полуосью, на которой
находится точка а.
,
по уравнению фазовой траектории
определяют координаты в точке следующего
пересечения фазовой траектории с
действительной полуосью, на которой
находится точка а.
![]()
z

b a y
Если
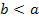 ,
причем
,
причем 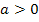 ,
то амплитуда колебаний уменьшается,
процесс затухает.
,
то амплитуда колебаний уменьшается,
процесс затухает.Если
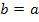 ,
имеется предельный цикл, амплитуда
постоянна.
,
имеется предельный цикл, амплитуда
постоянна.Если
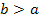 ,
то колебательный процесс расходится,
амплитуда возрастает.
,
то колебательный процесс расходится,
амплитуда возрастает.
Е сли
есть возможность, получают зависимость
.
сли
есть возможность, получают зависимость
.
b
b1
b2
a2 a1 a3 a
Для такого характера
![]() если
если ![]() ,
то процесс будет сходиться к 0.
,
то процесс будет сходиться к 0.
Если ![]() ,
то колебательный процесс будет сходиться
к
,
то колебательный процесс будет сходиться
к ![]() ,
и 1-й предельный цикл будет неустойчивым,
а 2-й – устойчивым.
,
и 1-й предельный цикл будет неустойчивым,
а 2-й – устойчивым.
Приближенные методы исследования автоколебаний
Метод гармонической линеаризации.
Рассмотрим на примере конкретной системы
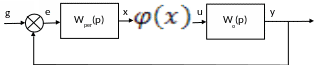
-
Предположим,
что на вход нелинейного звена поступает
гармонический сигнал ![]() .
.
Нелинейность имеет вид:
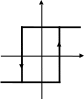 Q
Q
a
-b b х
-a
Рис.1
На выходе будет:
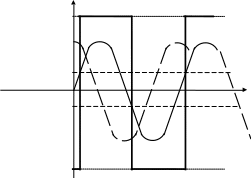
Q u
b
t1 t2 T t3 t
ψ1 π ψ2 2π ψ3 ψ
-b
-Q
![]()
![]()
Как видно, на выходе нелинейного звена получились прямоугольные 2-полярные колебания с периодом, равным Т.
Такие колебания, очевидно, можно представить с помощью ряда Фурье:
![]() ,
,
Где ![]()
![]()
Если линейная часть является инерционной системой с убывающей амплитудно-частотной характеристикой, то высшие гармоники сглаживаются линейной частью (имеем фильтр, т.к. убывающая амплитудная характеристика соответствует фильтру высоких частот). В этом случае в качестве выхода нелинейного звена можно рассматривать только первую гармонику, т.к. остальные все равно будут сглажены линейной частью.
Тогда ![]() .
.
В связи с тем,
что вид колебаний на выходе нелинейного
звена зависит от амплитуды входного
колебания, коэффициенты ![]() ,
,
![]() определяются амплитудой входного
сигнала.
определяются амплитудой входного
сигнала.
Введем новые коэффициенты:
![]() ,
,
![]() .
.
![]() ,
,
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Имеем некоторую
характеристику нелинейного звена ![]() ,
которая является аналогом частотной
характеристики линейного звена, поскольку
она изменяет амплитуду и фазу входного
гармонического сигнала, не изменяя
частоты. Но зависит эта характеристика
не от частоты колебаний, а от амплитуды.
,
которая является аналогом частотной
характеристики линейного звена, поскольку
она изменяет амплитуду и фазу входного
гармонического сигнала, не изменяя
частоты. Но зависит эта характеристика
не от частоты колебаний, а от амплитуды.
![]()
Фактически нелинейная система была сведена к линейной (линеаризована), и характеристика нелинейного звена равна .
Как известно,
в замкнутой линейной системе возникают
колебания в случае, когда комплексная
частотная характеристика разомкнутой
системы проходит через точку ![]() (при
устойчивой линейной части), т.е.:
(при
устойчивой линейной части), т.е.:
![]()
Если это
комплексное уравнение имеет действительные
корни ![]() ,
то в замкнутой нелинейной системе
возникают автоколебания.
,
то в замкнутой нелинейной системе
возникают автоколебания.
Решают уравнение либо численно, сведя его к 2-м скалярным уравнениям:
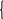
![]()
![]() ,
,
либо графически,
представив в виде ![]() , называемом уравнением Гольдфарба:
, называемом уравнением Гольдфарба:
Im

Re
WЛ(jω) -1/J(A)
Точки пересечения графиков дают корни уравнения A и ω.
![]() - эквивалентная частотная характеристика
(эквивалентная передаточная функция)
получается для конкретной статической
характеристики нелинейности (см. рис.1)
и выхода нелинейного звена u(t)
(рис.2) из коэффициентов ряда Фурье
следующим путем:
- эквивалентная частотная характеристика
(эквивалентная передаточная функция)
получается для конкретной статической
характеристики нелинейности (см. рис.1)
и выхода нелинейного звена u(t)
(рис.2) из коэффициентов ряда Фурье
следующим путем:
![]()
![]()
![]()
![]()
![]()
Чтобы упростить
интеграл, рассмотрим интервал ![]() .
Тогда
.
Тогда
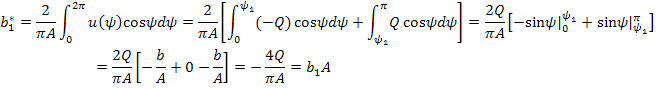
![]()
![]()

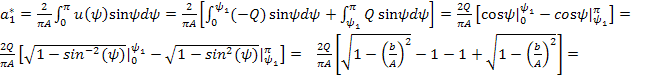
![]()
Разбивая интеграл
![]() на
участки :
на
участки : ![]()
![]()
Тогда
![]() .
.
Как видно, ![]() .
.
Определив коэффициенты ряда Фурье, необходимо найти значение уравнения:
.
,
т.е. определить значения ![]() ,
которые преобразуют уравнение в
тождество, для чего уравнение можно
разделить на скалярные:
,
которые преобразуют уравнение в
тождество, для чего уравнение можно
разделить на скалярные:
,
и найти все решения.
