
- •Нелинейные системы управления
- •Типовые нелинейности
- •Исследование переходных процессов в нелинейных системах
- •Исследование переходных процессов в нелинейных системах по фазовым портретам
- •Исследование колебательных процессов по фазовым траекториям
- •Метод точечных преобразований
- •Оценка устойчивости колебаний
- •Устойчивость замкнутых нелинейных систем
- •Синтез нелинейных систем
Исследование переходных процессов в нелинейных системах по фазовым портретам
Для линейных и нелинейных устойчивых систем переходные процессы в установившемся состоянии сходятся или к постоянным значениям или к некоторым установившемся колебательным процессам. При исследовании переходных процессов необходимо использовать достаточно протяженные графики. Переход к фазовым координатам позволяет в ряде случаев упростить анализ и синтез систем.
Фазовыми координатами в большинстве случаев являются выход объекта и функции выхода объекта, причем чаще всего используют в качестве функции производные от выхода (1-ю,2-ю).
В дальнейшем
будем рассматривать в качестве фазовых
координат ![]() :
:
![]()
Построение фазовых портретов
Фазовой
траекторией называют функцию ![]() ,
полученную для некоторых начальных
условий
,
полученную для некоторых начальных
условий ![]() .
.
Совокупность фазовых траекторий, полученных для различных начальных условий, называют фазовым портретом.
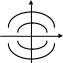 z
z



y
z – это скорость изменения y.
1. Фазовые траектории в верхней полуплоскости направлены слева направо, в нижней – справа налево.
2. Ось абсцисс фазовые траектории должны пересекать под прямым углом.
3. Через каждую точку фазовой плоскости (за исключением особых точек) проходит только 1 фазовая траектория.
Построение фазовых траекторий. Методы построения.
Численный метод
Реализуется
наиболее просто, т.к. для каждого значения
![]() производную можно определить одним из
приближенных методов
производную можно определить одним из
приближенных методов
![]()
![]()
Метод изоклин. Приближенный метод, рассчитанный на реализацию без компьютера.
Аналитический метод
Метод заключается в исключении времени из дифференциальных уравнений, описывающих систему.
Проблема состоит в том, что не все полученные вследствие этой операции уравнения, просто решаются. Пример «хорошего» уравнения
![]() .
.
Введем обозначение
![]()
![]() или
или
![]() .
Разделив левую часть последнего уравнения
на
.
Разделив левую часть последнего уравнения
на ![]() ,
а правую на z,
исключим время из уравнения:
,
а правую на z,
исключим время из уравнения: ![]()
![]()
![]()
![]()
Интегрирование возможно, если u является, например, дискретной функцией времени:
-a, x≤-b
![]() = 0, -b<x<b
= 0, -b<x<b
a, x≥b
Для этих 3-х случаев получаем 3 интеграла:
![]()
![]()
![]()
Константы получаем из начальных условий
![]()
![]()
![]() ,
,
![]() - это начальные значения фазовой
траектории, соответствующие начальному
значению u.
- это начальные значения фазовой
траектории, соответствующие начальному
значению u.
Для построения графиков изобразим переходные процессы и весовые функции реального интегрирующего звена.

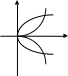 ka
y u=+a
ka
y u=+a
t
-ka u=-a
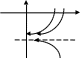 z
z
y
-ka
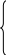
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
u=-a
 z
z
y
-ka
![]()
![]() ,
если
,
если ![]() ,
то
,
то ![]() =0.
=0.
u
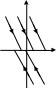 =0
=0
z
y
u=+a
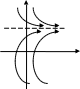 z
z
![]()
y
![]()
При изменении
![]() происходит изменение
происходит изменение ![]() ,
и при достижении
пороговых значений (
,
и при достижении
пороговых значений (![]() )
изменяется управляющее воздействие
(изменяется закон движения
)
изменяется управляющее воздействие
(изменяется закон движения ![]() ).
).
Процесс дискретного изменения закона движения называется переключением. Кривые или поверхности, на которых происходит переключение закона движения, называются линиями или поверхностями переключения.
Фазовая поверхность, соответствующая одному управления, называется листом.
Если закон изменяется многократно, получаем многолистные фазовые поверхности, которые стыкуются по линиям переключения.
Для рассмотренного примера линия переключения определяется в основном типом регулятора.
В простейшем случае, если имеется пропорциональный регулятор.
![]()
Условие переключения:
![]() ,
,
Тогда ![]()
![]()
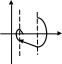 z
z
+a -a
y
+b -b
ПД-регулятор
![]()
![]()
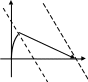
![]()
+b
![]() -b
-b

+a -a
+a
y
ПИД-регулятор
![]()
Линии переключения
в данном случае можно пытаться получить,
выражая интеграл ![]() из уравнения объекта, однако исключить
время можно только в том случае, если в
правой части уравнения будет стоять 0,
что соответствует очень редким состояниям.
из уравнения объекта, однако исключить
время можно только в том случае, если в
правой части уравнения будет стоять 0,
что соответствует очень редким состояниям.
При численном построении фазовых траекторий линии переключения можно построить, фиксируя точки переключения, получаемые численным методом, и аппроксимируя промежутки между точками прямой линией, параболой и т.д. Эти линии переключения существенно зависят от начальных значений фазовых траекторий. Для разных начальных условий будут получены различные линии переключения.
Связь между переходными процессами и фазовыми траекториями
Особые точки на фазовых портретах рассмотрим на примере звена второго порядка
![]()
Для консервативного звена:
![]()
![]()
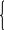
![]()
Делим 1-е уравнение на 2-е, получаем:
![]()
![]()
![]()
![]() - уравнение эллипса (
- уравнение эллипса (![]() ).
).
Очевидно, С может быть произвольным, зависящим от начальных условий.
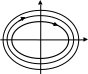 z
z
a

-b b y
-a
Полученное множество замкнутых линий в виде эллипса образует фазовый портрет.
Решение дифференциального уравнения имеет вид:
![]()
![]()
![]() определяются начальными условиями
определяются начальными условиями ![]() и
и
![]() .
.
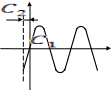

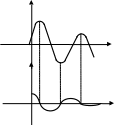
Если на фазовой характеристике имеются замкнутые циклы, переходный процесс будет представлять собой незатухающие колебания.
Центр замкнутого цикла, к которому сходятся фазовые траектории при уменьшении , называют особой точкой типа центр.
![]()
![]()
![]() )
)
y
t
z
t
Запишем уравнение фазовой траектории:
![]()
![]()
![]()
![]()
Получим нелинейное уравнение:
![]()
Построим фазовую
траекторию по графикам ![]() и
и ![]() ,
исключая время t.
,
исключая время t.

z
y
Как видно, если фазовая траектория, закручиваясь, сходится к некоторой точке на оси y, то переходный процесс будет колебательным и сходиться к соответствующему значению y.
Особая точка называется точкой типа фокус.
![]()
![]()
![]()
Для случая
введем
обозначение: ![]()
![]()
![]()
![]()
![]()
![]()
 z
z
y
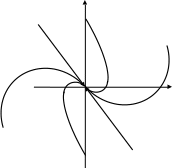
Особая точка (начало координат), где пересекаются фазовые траектории, называется точкой типа узел. Если знак перед вторым слагаемым в уравнении «минус», то переходные процессы будут расходящиеся, если , то переходной процесс будет колебательным с амплитудой, возрастающей до бесконечности, а для переходной процесс апериодический, уходящий в бесконечность. Соответственно, особые точки - неустойчивый фокус и неустойчивый узел.
Если![]() ,
а уравнение имеет вид:
,
а уравнение имеет вид:
![]()
![]()
![]()
![]()
![]()
Как видно, при увеличении t значения весовой и переходной функций уходят в бесконечность.
![]()
![]()
![]()
![]()
C=0,
![]()
z
y
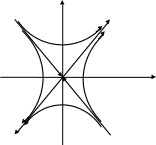
Начальная точка называется особой точкой типа седло.
