11 Вопрос Формула для вычисления скалярного произведения векторов через их координаты.
Утверждение:
Для векторов, заданных своими
координатами:
и
справедлива
формула:
.
Произносится:
Скалярное произведение векторов
равно сумме произведений соответствующих
координат.
Доказательство:
Запишем
каждый вектор в виде разложения по
базисным векторам:
Запишем
скалярное произведение:
Используем
свойство 7) :
Используем
свойство 6):
Напомним,
что
–
базисные вектора декартовой системы
координат, т.е. они попарно перпендикулярны,
значит, по свойству 2):
.
В
итоге получим:
Последний
шаг: по третьему свойству, зная, что
:
.
Замечание:
Для векторов на плоскости (двумерных)
справедлива аналогичная формула, т.е.
без последнего слагаемого:
и
:
.
Формула для вычисления угла между векторами.
Замечание:
Не столько угла, сколько косинуса
угла.
Итак, на данный момент, для
вычисления скалярного произведения
есть:
а) определение:
,
б)
выведенная чуть ранее формула:
.
Выразим
косинус угла между векторами из первого
равенства:
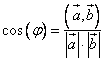Произносится:
косинус угла между векторами равен
отношению скалярного произведения к
произведению длин векторов.
А
вычислить скалярное произведение можно
про второй формуле. В результате получится
вот такая формула (её и следует запомнить
и применять для вычисления угла):
.
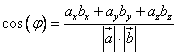На
следующей странице рассмотрим примеры
решения задач с использование свойств
и полученных формул.
12 Вопрос
Определение. Уравнение вида
Ах+Ву+С=0 (2)
при произвольных коэффициентах А, В, С (А и В одновременно не равны нулю) определяют некоторую прямую в прямоугольной системе координат. Данное уравнение называется общим уравнением прямой.
Уравнение (2) есть уравнение первой степени, таким образом, каждая прямая есть линия первого порядка и, обратно, каждая линия первого порядка есть прямая. Общее уравнение
Ax
+ By + C (
> 0).
Вектор
=
(А; В)
- нормальный вектор прямой.
В
векторном виде:
+
С = 0,
где
-
радиус-вектор произвольной точки на
прямой (рис. 4.11).
Частные случаи:
1) By + C = 0 - прямая параллельна оси Ox;
2) Ax + C = 0 - прямая параллельна оси Oy;
3) Ax + By = 0 - прямая проходит через начало координат;
4) y = 0 - ось Ox;
5) x = 0 - ось Oy.
13 Вопрос
п.1. Уравнение прямой с угловым коэффициентом.
Пусть дана прямая L на координатной плоскости Оху.
Определение. Углом наклона прямой к оси абсцисс называется угол поворота оси абсцисс вокруг любой ее точки против часовой стрелки до положения параллельности (или совпадения) с данной прямой.
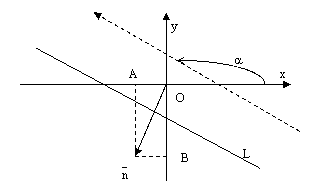
рис.1.
Из
определения
следует, что угол
наклона
прямой
L к оси Ох может изменяться от нуля до
:
.
Если прямая
,
то
.
Пусть
(1)
– общее
уравнение прямой L, где
–
нормальный вектор прямой L и
.
Тогда
и
(см.
рис.1). Выразим у из уравнения
(1)
.
,
.
Уравнение прямой L принимает вид:
.
Определение. Уравнение прямой вида
(2)
называется уравнением прямой с угловым коэффициентом, а коэффициент k называется угловым коэффициентом данной прямой.
Теорема. В уравнении прямой с угловым коэффициентом
угловой коэффициент k равен тангенсу угла наклона прямой к оси абсцисс:
.
(3)
Доказательство.
1) Если прямая
,
то
и
.
С другой стороны, ее нормальный вектор
и
.
Тогда
и,
следовательно,
,
ч.т.д.
2)
Пусть
,
тогда
,
и
.
Пусть F – точка пересечения прямой L с
осью
абсцисс. Тогда
,
.
Опишем
окружность единичного радиуса с центром
в точке F , а в точке оси Ох с координатой
проведем
касательную m к этой окружности. См.
рис.2.
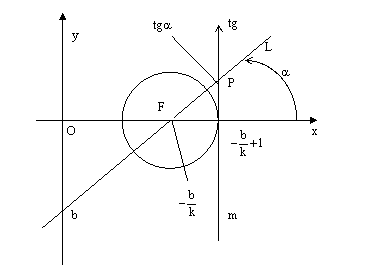
рис.2.
Выберем
положительное направление на прямой
m, так, чтобы
.
Тогда ось m является осью
тангенсов для данной единичной
(тригонометрической) окружности.
Пусть
Р – точка пересечения прямой L с осью
тангенсов m. Тогда, с одной стороны,
,
где
–
угол
наклона прямой L к оси Ох, а, с другой
стороны, точка
и
,
откуда и следует равенство
,
ч.т.д.
Теорема доказана.
Заметим,
что приведенное доказательство
принадлежит автору этих лекций.
Достоинством этого доказательства
является то, что оно не зависит ни от
величины угла наклона
,
ни от величины коэффициента
.
В заключение отметим, что коэффициент b в уравнении (2) равен величине отрезка, отсекаемого прямой от оси ординат (см. рис.2