Ответы по высшей математике на вопросы

7 вопрос

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].

Описание метода

Пусть исходная система выглядит следующим образом

Матрица называется основной матрицей системы,  — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

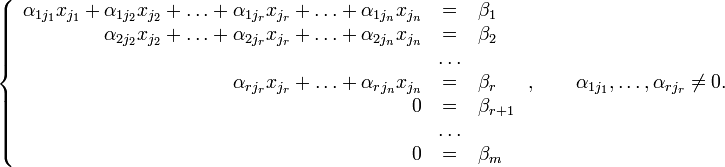
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных ^[3].

Тогда переменные называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число , где , то рассматриваемая система несовместна.

Пусть для любых .

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом ( , где  — номер строки):

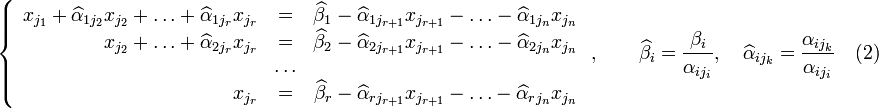, где

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной.

Условие совместности

Упомянутое выше условие для всех может быть сформулировано в качестве необходимого и достаточного условия совместности:

Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).

Теорема Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия: Количество главных переменных равно рангу системы и не зависит от её решения. Если ранг совместной системы равен числу переменных данной системы, то она определена.

Алгоритм

Описание

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

• На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

• На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует порядка действий.

Этот метод опирается на:

Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.

Простейший случай

В простейшем случае алгоритм выглядит так:

• Прямой ход:

• Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.

Пример

Покажем, как методом Гаусса можно решить следующую систему:

Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

из третьего;

из второго, подставив полученное

из первого, подставив полученные и .

8 Вопрос

 Под вектором в элементарной математике понимают направленный отрезок. Этот отрезок изображается стрелкой и обозначается или одной буквой со стрелкой ( )

Операции над векторами

Сложение

Операцию сложения геометрических векторов можно определить несколькими в принципе эквивалентными способами, каждый их которых однако может быть удобнее или естественнее в зависимости от ситуации и типа рассматриваемых векторов. Так, правило треугольника наиболее простое и геометрически фундаментальное, удобно для сложения любого количества векторов, однако правило параллелограмма более удобно для фиксированных или скользящих векторов, т.к. не требует переноса второго слагаемого (что в принципе могло бы смущать или запутывать в этих случаях) для построения суммы, т.е. удобно для сложения векторов с началом в одной точке, в добавок имея то преимущество, что в нем более очевидно равноправие слагаемых; координатное же определение, являясь простым и удобным, бывает очень полезно для вычислений.

Два вектора u, v и вектор их суммы

Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти векторы переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего - с концом второго итд, сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (т.е. изображается направленным отрезком, замыкающим ломаную).

Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

Сложение векторов с использованием координат. Каждая координата (см. Базис и разложение по базису) суммы векторов есть сумма соответствующей координаты всех (двух или более) суммируемых векторов. Например, для двумерного случая:

(Могут быть использованы прямоугольные или косоугольные координаты; правило сложения остаются одинаковыми для обоих этих типов координат).

• Модуль (длину) вектора суммы можно вычислить, например, используя теорему косинусов где  — угол между отрезками, изображающими данные векторы, когда начало одного вектора совпадает с концом другого. Или: где  — угол между векторами (выходящими из одной точки).

Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.

Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.

Сложение коллинеарных скользящих векторов

Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные векторы. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы

Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).

Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.

Вычитание

Операция вычитания из вектора ветора сводится к сложению первого вектора и вектора, противоположного второму:

(Само сложение при этом осуществляется так, как описано в параграфе выше, пользуясь, если это удобно, любым из приведенных там альтернативных способов).

Однако легко видеть, что из правила треугольника можно получить и отдельное геометрическое определение разности. Для этого достаточно посмотреть на чертеж, иллюстрирующий сложение по правилу треугольника и осознать, что разность векторов и на этом чертеже есть вектор Отсюда прямо формулируется правило треугольника для вычитания векторов:

разность двух векторов с общим началом (или перенесенных параллельно так, чтобы начала совпали) есть вектор с началом, совпадающим с концом вычитаемого и концом, совпадающим с концом уменьшеаемого.

Это правило также может быть удобным.

Скалярное произведение

Основная статья: Скалярное произведение

Скалярное произведение двух векторов

Скалярное произведение на множестве геометрических векторов вводится, как

Скалярное произведение любого вектора и какого-то единичного вектора есть проекция (ортогональная проекция) вектора на направление этого единичного вектора:

Легко видеть, что скалярное произведение может быть записано через операцию (ортогонального) проецирования:

(где  — проекция вектора на направление ,  — проекция вектора на направление ).

• В абстрактном подходе обычно сперва вводят скалярное произведение, а уже через него определяют понятие угла, ортогональность, ортогональную проекцию.

Векторное произведение

Основная статья: Векторное произведение

Векторное произведение двух векторов

Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:

• длина вектора равна произведению длин векторов и на синус угла φ между ними

• вектор ортогонален каждому из векторов и

• вектор направлен так, что тройка векторов является правой.

Обозначение:

Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.

Свойства векторного произведения:

1. При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е

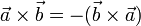
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть

3. Векторное произведение обладает распределительным свойством: