44.Исследование функции 2х перемен-ых на локальный экстремум.

Необходимое условие локального экстремума дифференцируемой функции: Если(x₀ ,y₀)-точка экстремума функции f, то 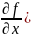x_0,y₀)=0 и 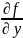(x_0,y₀)=0 Достаточные условия локального экстремума дважды дифференцируемой функции О бозначим Если D > 0, A > 0, то(x0 ,y0) - точка минимума. Если D > 0, A < 0, то (x0 ,y0) - точка максимума. Если D < 0, экстемума в точке(x0 ,y0) нет. Если D = 0, необходимы дополнительные исследования.

45.Мнимая единица и комплексные числа. Комплексная плоскость и бесконечно большое комплексное число.Опр.1 Комплексным числом z называется выражение вида z=х+iу, где х и у — действительные числа, a i — так называемая мнимая единица, i²=-1. Если x=0, то число 0+iy=iy называется чисто мнимым; если у=0, то число х+i0=х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. e. RÌС. Мнимая единица — это число, квадрат которого равен −1. Т.е. i — это одно из решений уравнения Число х называется действительной частью комплексного числа z и обозначается х=Re z, а у — мнимой частью z, у = Im z. Два комплексных числа z₁=x₁+iy₁ и z₂=х₂+iy₂ называются равными (z₁=z₂) тогда и только тогда, когда равны их действительные части и равны их мнимые части: х₁=х₂, y₁=у₂. В частности, комплексное число z=х+iy равно нулю тогда и только тогда, когда х=у=0. Понятия «больше» и «меньше» для комплексных чисел не вводятся. Два комплексных числа z=х+iy и z=х-iy, отличающиеся лишь знаком мнимой части, называются сопряженными. Опр2. Координатная плоскость, каждая точка которой отождествлена с комплексным числом, называется комплексной плоскостью. Ось абсцисс Ох называется действительной осью, Ось ординат Оу называется мнимой осью. Замеч. Существует взаимно однозначное соответствие между точками координатной плоскости и их радиус-векторами. Поэтому также существует взаимно однозначное соответствие и между всеми комплексными числами и радиус-векторами соответствующих точек комплексной плоскости. Итак, чтобы изобразить комплексное число z точкой на комплексной плоскости нужно записать его в алгебраической форме записи, найти его действительную и мнимую части и построить в ПДСК на этой плоскости точку, абсцисса которой равна действительной части, а ордината – мнимой части данного комплексного числа z: z=a+bi↔z(a,b) ↔Ozвектор, где векторOz является радиус-вектором точки z.

46. Алгебраическая, тригонометрическая и показательная формы комп-го числа. 1.Пусть x и y – обычные числа. Число вида z=x+iy называется комплексным числом в алгебраической форме. x называют вещественной или действительной частью числа z и обозначают так:x=Re(z); y называют мнимой частью числа z и обозначают так:x=lm(z).Число Ẑ=x-iy. называют комплексно сопряженным числу z. Действует следующее общее правило: «чтобы получить число, комплексно сопряженное данному, надо в нем заменить i на –i ». 2. С геометрической интерпретацией связана и еще одна форма записи комплексных чисел, называемая тригонометрической формой их записи. Соединим точку (x, y) с началом координат отрезком прямой. Длина этого отрезка r называется модулем комплексного числа z и обозначается | z | или mod(z). 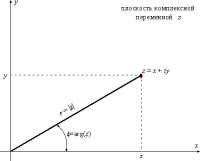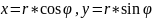Угол j, который этот отрезок образует с осью ОХ, называется аргументом комплексного числа z и обозначается arg(z).Из рисунка ясно, что имеют место соотношения 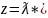- Эта форма и получила название комплексного числа в тригонометрической форме. 3. Одна из важнейших формул математического анализа – формула Эйлера – имеет вид 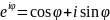С учетом тригонометрической формы комплексного числа его теперь можно представить в виде или, с учетом того, что аргумент определяется с точностью до 2p,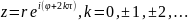 Эта форма записи помогает, например, определить логарифм комплексного числа

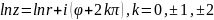
47. Операции над комплесными числами. Логарифм компле-го числа. 1.Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a=c и b= d. 2.Суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d). 3.Произведением двух комплексных чисел a+ ib и c+id назы-ся комп-ное число ac–bd + i(ad +bc). Эти операции обладают следующими свойствами:

1. Коммутативность сложения: z₁+ z₂= z₂+z₁, для любых z_1, z₂

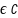
2. Ассоциативность сложения: (z1 + z2) + z3 = z1 + (z2 + z3), для любых z_1, z₂

3. Существует такое число z = 0, которое обладает свойством z + 0 = z, для любого z .

4. Для любых двух чисел z1 и z2 существует такое число z, что z1 + z = z2. Такое число z называется разностью двух комплексных чисел и обозначается z = z2 – z1.

5. Коммутативность умножения: z1z2 = z2z1, для любых z_1, z₂

6. Ассоциативность умножения: (z1z2)z3 = z1(z2z3), для любых z_1,z_2,z₃

7. Дистрибутивность сложения относительно умножения: z1(z2 + z3) = z1z2 + z1z3, для любых z_1,z_2,z₃ 8. Для любого комплексного числа z:z · 1 = z. 9. Для любых двух чисел z₁иz₂существует такое число z, что z₁*z=z₂. Такое число z называется частным двух комплексных чисел и обозначается z=z₂\z₁. Деление на 0 невозможно.

Для комплексных чисел логарифм определяется так же, как вещественный. На практике используется почти исключительно натуральный комплексный логарифм, который обозначается Ln zи определяется как решение w уравнения e^w=z. Комплексный нуль не имеет логарифма, поскольку комплексная экспонента не принимает нулевого значения. Ненулевое z можно представить в показательной форме. Kомплексный логарифм Ln z существует для любого z , и его вещественная часть определяется однозначно, в то время как мнимая часть имеет бесконечное множество значений, различающихся на целое кратное 2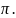

48.Многочлены.Разложение многочленов на множители.Многочленом называется сумма одночленов. Если все одночлены в многочлене приведены к стандартному виду, то говорят, что это многочлен стандартного вида. Алгебраическое выражение, не содержащее операции деления и извлечения корня (такое выражение называется целым), всегда может быть приведено к многочлену стандартного вида. Степенью многочлена называется наибольшая из степеней его слагаемых.Имеет смысл говорить о разложении многочлена на множители, если его степень не ниже второй.Теорема. Любой многочлен степени n вида P_n(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀ представляется произведением постоянного множителя при старшей степени a_n и n линейных множителей (x-x₁), i=1, 2, …, n, то есть P_n(x)=a_n(x-x_n)(x-x_n-1)…(x-x₁) причемX_i , i=1, 2, …, n являются корнями многочлена. Эта теорема сформулирована для комплексных корней X_i , i=1, 2, …, n и комплексных коэффициентов a_k , k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители. Если коэффициенты a_k , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.Замечание. Среди корней многочлена могут быть повторяющиеся. Доказательство теоремы проводится с использованием основной теоремы алгебры и следствия из теоремы Безу.Разложение на множители квадратного трехчлена. Квадратный трехчлен ax²+bx+c раскладывается на два линейных множителя: ax²+bx+c=a(x-x₁)(x-x₂), где х_{1 и} х₂ являются корнями (комплексными или действительными).Таким образом, разложение на множители квадратного трехчлена сводится к решению квадратного уравнения.Способы разложения на множители многочлена степени выше второй.В общем случае эта задача предполагает творческий подход, так как не существует универсального метода ее решения. Но все же попробуем дать несколько наводок. В подавляющем числе случаев, разложение многочлена на множители основано на следствии из теоремы Безу, то есть находится или подбирается корень и понижается степень многочлена на единицу делением на . У полученного многочлена ищется корень и процесс повторяется до полного разложения. Если же корень найти не удается, то используются специфические способы разложения: от группировки, до ввода дополнительных взаимоисключающих слагаемых.