
- •32. Правило Лопиталя
- •12.Операция над пределами последовательностей.
- •13.Пределы функции в точке. Односторонние пределыв.
- •15.Бесконечно малые и бесконечно большие функции.
- •16.Замечательные пределы.(I) зам предел: (II) зам предел : (III)зп: (IV)зп: (V) зп:
- •18.Непрерывность функции одной переменньой в точке .Односторонняя непрерывность
- •23 Точки разрыва функции и их классификация
- •32. Правило Лопиталя
- •33. Локальный и глобальный экстремум функции
- •35. Асимптоты графика функций.
- •36. Алгоритм полного исследования функции для построения её графика.
- •37. Функции двух переменных, геометрический смысл. Линии уровня поверхности.
- •38. Предел и непрерывность функции двух переменных.
- •39.Частные производные. Уравнение касательной плоскости и нормали к поверхности.
- •44.Исследование функции 2х перемен-ых на локальный экстремум.
- •49. Выделение целой части неправильной алгебраической дроби.
- •58.Определенный интеграл с переменным верхним пределом и его свойства
- •71.Простейшие св-ва рядов.Необходимый признак сходимости.
- •72.Признаки сх-ти рядов с положительными членами.
- •73.Знакопеременные ряды,абсолютная и условная сх-ти
- •74.Признак Лейбница сходимости знакочередующегося ряда.
- •75.Функциональные ряды.Нахождение области сх-ти функционального ряда.
- •76.Степенные ряды.Теорема Абеля.
- •77.Радиус и интервал сх-ти степенного ряда.
- •78.Дифференцирование и интегрирование степенных рядов.
32. Правило Лопиталя
Правило
Лопиталя представляет
собой метод вычисления пределов, имеющих
неопределенность
типа![]() или
или![]() .
Пусть a
является некоторым конечным действительным
числом или равно бесконечности. Если
.
Пусть a
является некоторым конечным действительным
числом или равно бесконечности. Если
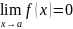 и
и
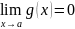 ,
то
,
то
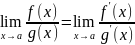 ;
если
;
если
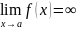 и
и
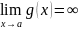 ,
то аналогично
Правило
Лопиталя можно также применять к
неопределенностям типа 0*
,
то аналогично
Правило
Лопиталя можно также применять к
неопределенностям типа 0*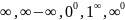 .
Первые две неопределенности
.
Первые две неопределенности
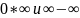 можно свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности
можно свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности
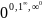 сводятся
к типу
сводятся
к типу
![]() с
помощью соотношения
с
помощью соотношения
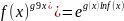
33. Локальный и глобальный экстремум функции
Определение. Точка x0 называется точкой локального максимума функции f ( x) , если существует такая окрестность точки x0 , что для всех x из этой окрестности f (x) f (x0 ).
Определение. Точка x0 называется точкой локального минимума функции f ( x) , если существует такая
окрестность точки x0 , что для всех x из этой окрестности f (x) f (x0 ).Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Максимум и минимум функции называются её локальными экстремумами. Термин "локальный экстремум" обусловлен тем, что введённое понятие экстремума связано с окрестностью данной точки в области определения функции, а не со всей этой областью. Функция может иметь несколько экстремумов, причём минимум в одной точке может быть больше максимума в другой. Определение. Точка x0 называется точкой строгого локального максимума функции f (x) , если существует такая окрестность точки x0 , что для всех x из этой окрестности f (x) f (x0 ). Определение. Точка x0 называется точкой строгого локального минимума функции f ( x) , если существует такая окрестность точки x0 , что для всех x из этой окрестности f (x) f (x0 ) Наибольшее (наименьшее) значение функции на промежутке называется глобальным экстремумом. Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
34. Выпуклость и вогнутость графика функций. Точки перегиба.График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
35. Асимптоты графика функций.
Говорят,
что прямая x=a является
вертикальной асимптотой графика
непрерывной функции y=f(x),
если хотя бы один из пределов
![]() равен
∞.
равен
∞.
Если
функция y=f(x) задана
для
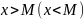 ,
то говорят, что прямая y=kx+b является
наклонной асимптотой непрерывной
кривой y=f(x) при
,
то говорят, что прямая y=kx+b является
наклонной асимптотой непрерывной
кривой y=f(x) при
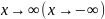 ,
если f(x)=kx+b+a(x)
, где
,
если f(x)=kx+b+a(x)
, где
![]() ,
т. е.
,
т. е.
![]() -
бесконечно малая функция при
-
бесконечно малая функция при
![]() Т
е о р е м а. Для того чтобы график функции
y=f(x) имел
при
Т
е о р е м а. Для того чтобы график функции
y=f(x) имел
при
![]()
![]() наклонную
асимптому, необходитмо и достаточно,
чтобы существовали конечные пределы
наклонную
асимптому, необходитмо и достаточно,
чтобы существовали конечные пределы
![]() ,
,
и
тогда прямая
![]() есть
асимптота
есть
асимптота
