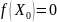- •32. Правило Лопиталя
- •12.Операция над пределами последовательностей.
- •13.Пределы функции в точке. Односторонние пределыв.
- •15.Бесконечно малые и бесконечно большие функции.
- •16.Замечательные пределы.(I) зам предел: (II) зам предел : (III)зп: (IV)зп: (V) зп:
- •18.Непрерывность функции одной переменньой в точке .Односторонняя непрерывность
- •23 Точки разрыва функции и их классификация
- •32. Правило Лопиталя
- •33. Локальный и глобальный экстремум функции
- •35. Асимптоты графика функций.
- •36. Алгоритм полного исследования функции для построения её графика.
- •37. Функции двух переменных, геометрический смысл. Линии уровня поверхности.
- •38. Предел и непрерывность функции двух переменных.
- •39.Частные производные. Уравнение касательной плоскости и нормали к поверхности.
- •44.Исследование функции 2х перемен-ых на локальный экстремум.
- •49. Выделение целой части неправильной алгебраической дроби.
- •58.Определенный интеграл с переменным верхним пределом и его свойства
- •71.Простейшие св-ва рядов.Необходимый признак сходимости.
- •72.Признаки сх-ти рядов с положительными членами.
- •73.Знакопеременные ряды,абсолютная и условная сх-ти
- •74.Признак Лейбница сходимости знакочередующегося ряда.
- •75.Функциональные ряды.Нахождение области сх-ти функционального ряда.
- •76.Степенные ряды.Теорема Абеля.
- •77.Радиус и интервал сх-ти степенного ряда.
- •78.Дифференцирование и интегрирование степенных рядов.
12.Операция над пределами последовательностей.
Арифмитические операции над пределами сходящихся последовательностей:
Пусть
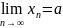 ,
,
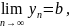 a
и b-конечные
числа,тогда:1)
a
и b-конечные
числа,тогда:1)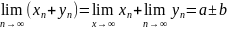 ; 2)
; 2)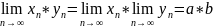 ;3)
;3)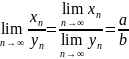 ,
если b
,
если b
13.Пределы функции в точке. Односторонние пределыв.
Опр1:Точка
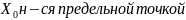 м-ва Х,если любая окрестность одержит
точки мн-ва Х отличное от (.)
м-ва Х,если любая окрестность одержит
точки мн-ва Х отличное от (.)
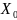
Предельная точка может принадлежать и не принадлежать
Число
А-предел ф-ции в точке
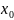 , если для любого Е
, если для любого Е 0
найдется положительное число
0
найдется положительное число
 ,
зависящая от Е , такое что
,
зависящая от Е , такое что
 ,как
только │
,как
только │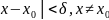
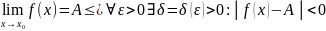 При
│x-
При
│x-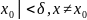
Односторонние
пределы.Опр2Левым пределом ф-ции f(x)
в точке
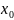 называется
называется
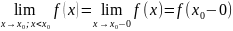 Опр3.Правым пределом f(x)
в точке
называется
Опр3.Правым пределом f(x)
в точке
называется
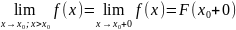 ТЕОРЕМА:Для того чтобы пределы
ТЕОРЕМА:Для того чтобы пределы
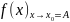 н и д чтобы в точке
существовали односторонние пределы
F(
н и д чтобы в точке
существовали односторонние пределы
F(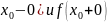 и оба были равны числу А
и оба были равны числу А

14.
Операции над пределами ф-ции.Пусть
f(x)
имеют конечные пределы ы точке
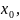 т.е.
т.е.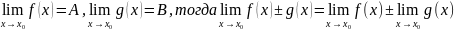
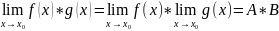
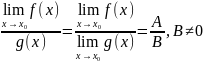
15.Бесконечно малые и бесконечно большие функции.
Опр1.Ф-ция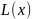 н-ся БМ при
н-ся БМ при
 .
Опр2. Ф-ция
.
Опр2. Ф-ция
 если
если
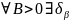 .
.
 при
при
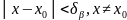
16.Замечательные пределы.(I) зам предел: (II) зам предел : (III)зп: (IV)зп: (V) зп:
17.Срачнение
бесконечо малых функций.Пусть
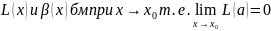 ,
,
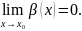 Опр1: говорят,что
Опр1: говорят,что
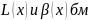 одного порядка малости, если
одного порядка малости, если
 ;
Опр2.говорят, что
;
Опр2.говорят, что
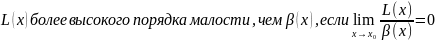 ; опр3.говорят, что
; опр3.говорят, что
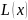 k-того
порядка малости по отношению к
k-того
порядка малости по отношению к
 ,
если
,
если
 ;
Опр4:БМ
;
Опр4:БМ
 н-ся эквивалентные,если
н-ся эквивалентные,если
18.Непрерывность функции одной переменньой в точке .Односторонняя непрерывность
Пусть
 определенана мн-ве
определенана мн-ве
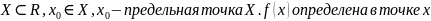 .
F(x)-
непрерывная в точке
,если
.
F(x)-
непрерывная в точке
,если
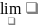 ф-ции
в точке
совпадает со значением ф-ции в точке
ф-ции
в точке
совпадает со значением ф-ции в точке
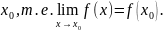 опр2.f(x)
н-ся непрерывной в точке
,
если
опр2.f(x)
н-ся непрерывной в точке
,
если
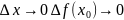 (
опр.непрерывсности на языке прирощения)
(
опр.непрерывсности на языке прирощения)
19.Свойства
в ф-ции.Непрерывность в точке. Поскольку
точки
непрерывности
функцииf(x) задаются
условием 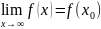 ,
то часть свойств функций, непрерывных
в точке
,
следует непосредственно из свойств
пределов. Сформулируем их в виде
следующей теоремы. Т 1 Пусть
ф-ииf(x)
g(x) непрерывны
в точке
.
Тогда функции
,
то часть свойств функций, непрерывных
в точке
,
следует непосредственно из свойств
пределов. Сформулируем их в виде
следующей теоремы. Т 1 Пусть
ф-ииf(x)
g(x) непрерывны
в точке
.
Тогда функции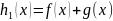
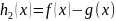 ,
, 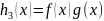 непрерывны в точке
.
Если
непрерывны в точке
.
Если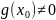 ,
то функция
,
то функция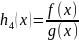 также
непрерывна в точке
также
непрерывна в точке ![]() . Как
непосредственное следствие этой теоремы
получается следующее Рассмотрим
множество всех функций, определённых
в некоторой фиксированной
окрестности
. Как
непосредственное следствие этой теоремы
получается следующее Рассмотрим
множество всех функций, определённых
в некоторой фиксированной
окрестности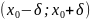 точки
и
непрерывных в этой точке. Тогда это
множество
точки
и
непрерывных в этой точке. Тогда это
множество
 является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
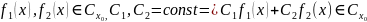 Доказательство.
Действительно, постоянные
Доказательство.
Действительно, постоянные
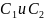 это
непpеpывные функции (в любой точке); по
пpедыдущей теоpеме тогда непpеpывны в
точке
пpоизведения
это
непpеpывные функции (в любой точке); по
пpедыдущей теоpеме тогда непpеpывны в
точке
пpоизведения
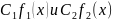 .
Но тогда по этой же теоpеме непpеpывна
в точке
и
сумма
.
Но тогда по этой же теоpеме непpеpывна
в точке
и
сумма
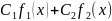 .
Т 2 Пусть
функции f и g таковы,
что существует композиция
.
Т 2 Пусть
функции f и g таковы,
что существует композиция
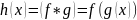 ,
,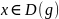 .
Пусть функция g
непрерывна в точке
.
Пусть функция g
непрерывна в точке
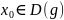 ,
а функция f
непрерывна в соответствующей
точке
,
а функция f
непрерывна в соответствующей
точке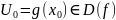 .
Тогда композиция h=f*g непрерывна
в точке
.
Доказательство.
Заметим, что равенство
.
Тогда композиция h=f*g непрерывна
в точке
.
Доказательство.
Заметим, что равенство
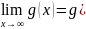 означает,
что при
означает,
что при
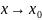 будет
будет
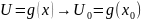 .
Значит,
.
Значит,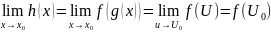 (последнее
равенство следует из непрерывности
функции f в
точке
(последнее
равенство следует из непрерывности
функции f в
точке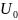 ).
Значит,
).
Значит, ,
а это равенство означает, что композиция
,
а это равенство означает, что композиция
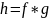 непрерывна
в точке
.
Заметим,
что, очевидно, в предыдущих двух теоремах
можно было бы заменить базу
на
односторонние базы
непрерывна
в точке
.
Заметим,
что, очевидно, в предыдущих двух теоремах
можно было бы заменить базу
на
односторонние базы
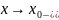 или
или  и
получить аналогичные утверждения для
непрерывности слева или
справа: Т 3 Пусть
функцииf(x) и
g(x) непрерывны
слева (справа) в точке
.
Тогда функции
,
,
непрерывны
слева (соотв. справа) в точке
.
Если g(
и
получить аналогичные утверждения для
непрерывности слева или
справа: Т 3 Пусть
функцииf(x) и
g(x) непрерывны
слева (справа) в точке
.
Тогда функции
,
,
непрерывны
слева (соотв. справа) в точке
.
Если g(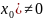 ,
то функция
также
непрерывна слева (спpава) в
точке
. Т 4 Пусть
функция g(x) непрерывна
слева (справа) в точке
,
а функция f(U) непрерывна
в точке
,
то функция
также
непрерывна слева (спpава) в
точке
. Т 4 Пусть
функция g(x) непрерывна
слева (справа) в точке
,
а функция f(U) непрерывна
в точке
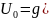 .
Тогда композицияh=f*g непрерывна
слева (соотв. справа) в точке
.
Тогда композицияh=f*g непрерывна
слева (соотв. справа) в точке
20.Непрерывность сложной, обратной ф-цй. Теорема 1(арифметич.Операции над непрерывными ф-ми). Пусть ф-ииf(x) и g(x) непрерывны в т.x0. Тогда, в т.x0 будут непрерывными: 1.f(x)±g(x) 2.f(x)∙g(x) 3.f(x)/g(x), еслиg(x)≠0. lim(x→x0) f(x)/g(x)=lim(x→x0) f(x)/lim(x→x0) g(x)=f(x0)/g(x0), если g(x0)≠0. Теорема 2.(непрерывность сложной ф-ии). Пусть ф-ияy=f(U) непрерывна в т.U0, а ф-ияU=ϕ(x)непрерывна в т.x0, причём ϕ(x0)=U0. Тогда, сложная ф-ияy=f(ϕ(x)) непрерывна в т.x0 и lim(x→x0) y(x)=lim(x→x0) f(ϕ(x))=f(ϕ(x0)), при этом lim(x→x0) f(ϕ(x))=f(lim(x→x0) ϕ(x))=f(ϕx0)) –возможен предельный переход под знаком непрерывной ф-ии. Теорема 3. Y=f(x) имеет обратную ф-июx=f-1(y) и непрерывна в т.x0∈X. Тогда, обратная ф-ияx=f-1(y) будет непрерывнав т.y0=f(x0). Теорема 4 (о сохр-и знаканепрерывной ф-ии). Пусть ф-ияf(x) непрерывна в т.x0, и f(x0)>0, тогда сущ-ет окрестность в т.x0 (x0-δ, x0+δ), в кот. f(x) тоже будет>0.
21
Непрерывность функции на множестве.
Непрерывность элементарных функций.Опр1.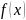 н-ся непрерывной на мн-ве Х, если она
не прерывна в каждой точке этого мн-ва.
Непрерывность нек ф-ций:
н-ся непрерывной на мн-ве Х, если она
не прерывна в каждой точке этого мн-ва.
Непрерывность нек ф-ций: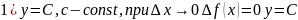 2)y=x
, при
2)y=x
, при
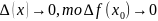 (
у=х непрерывна на всей числовой оси)3)
(
у=х непрерывна на всей числовой оси)3)
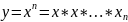 Эта
ф-ция непрерывна на всей числовой оси,
как произведение непрерывных
мн-телей.4)Целая рациональная ф-ция
Эта
ф-ция непрерывна на всей числовой оси,
как произведение непрерывных
мн-телей.4)Целая рациональная ф-ция
 Непрерывная
ф-ция на всей числовой оси, как сумма
непрерывных слагаемых(каждое слагаемое
есть произведение непрерывных ф-ций
постоянной, степенной)5)Дробно-рациональная
ф-ция
Непрерывная
ф-ция на всей числовой оси, как сумма
непрерывных слагаемых(каждое слагаемое
есть произведение непрерывных ф-ций
постоянной, степенной)5)Дробно-рациональная
ф-ция
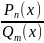 отношение
2-х многочленов непрерывно в тех точках,
где знаменатель
.6)y=sinx(тригонометрическая)
Из опр непрерывности ф-ции на языке
прирощений следует, что y=sinx-непрерывна
в люб точке числовой оси. 7) y=cosx-непрерывна
, как сложная ф-ция от двух непрерывных
ф-ций.8)y=tgx,
y=ctgx- непрерывны в своей области
определения.9) обратные тригонометрические
ф-ции непрерывны-по теореме о непрерывности
обратной ф-ции. Т1:Всякая элементарная
ф-ция непрерывна в своей области
определения.
отношение
2-х многочленов непрерывно в тех точках,
где знаменатель
.6)y=sinx(тригонометрическая)
Из опр непрерывности ф-ции на языке
прирощений следует, что y=sinx-непрерывна
в люб точке числовой оси. 7) y=cosx-непрерывна
, как сложная ф-ция от двух непрерывных
ф-ций.8)y=tgx,
y=ctgx- непрерывны в своей области
определения.9) обратные тригонометрические
ф-ции непрерывны-по теореме о непрерывности
обратной ф-ции. Т1:Всякая элементарная
ф-ция непрерывна в своей области
определения.
22
Свойства функций, непрерывных на
отрезке.
Т1:Если ф-ция непрерывна на отрезке
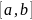 ,то
на этом отрезке она ограничена. Т2: Если
f(x)
непрерывна на отрезке
,то
на этом отрезке достигает своих
наибольшего и наименьшего значений.Т3(о
промежуточном значении непрерывности
ф-ции) Пусть f(x)
неприрывна на отрезке
,
,то
на этом отрезке она ограничена. Т2: Если
f(x)
непрерывна на отрезке
,то
на этом отрезке достигает своих
наибольшего и наименьшего значений.Т3(о
промежуточном значении непрерывности
ф-ции) Пусть f(x)
неприрывна на отрезке
,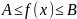 ,
тогда для
,
тогда для
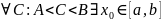 ,в
которой
,в
которой
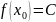 .
Т4: Пусть ф-ция y=f(x) непрерывна на отрезке
и на концах этого отрезка принимает
значения разных знаков, тогда
.
Т4: Пусть ф-ция y=f(x) непрерывна на отрезке
и на концах этого отрезка принимает
значения разных знаков, тогда
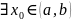 ,
в которой
,
в которой