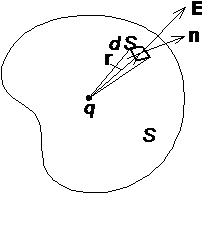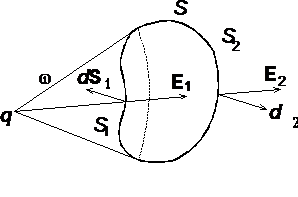1. Электрический заряд и его свойства. Электрическое поле. Напряженность и индукция электрического поля. Закон Кулона. Теорема Гауса.

Электрический заряд – это физическая величина, характеризующая электромагнитное взаимодействие. Тело заряжено отрицательно, если на нем избыток электронов, положительно – дефицит.

Свойства.

1)Существование в двух видах. Отрицательные и положительные. Разноименные заряды притягиваются, одноименные отталкиваются. Носителем элементарного, т.е. наименьшего, отрицательного заряда является электрон, заряд которого q_e= -1,6*10^-19Кл, а масса m_е=9,1*10^-31кг. Носителем элементарного положительного заряда является протон q_р=+1,6*10^-19Кл, масса m_р=1,67*10^-27кг.

2)Дискретность(квартование) электрического заряда.  Это означает, что заряд любого тела кратен заряду электрона q=Nq_e, где N – целое число. Однако мы, как правило, не замечаем дискретности заряда, так как элементарный заряд очень мал.Существуют частицы с дробным зарядом-кварки.В свободном состоянии кварки не существуют.

3)Сохранение заряда. В изолированной системе электрический заряд сохраняется. Закон сохранения зарядов – в замкнутой системе алгебраическая сумма зарядов не изменяется. Этот экспериментально установленный факт называется законом сохранения электрического заряда. Нигде и никогда в природе не возникает и не исчезает заряд одного знака. Появление каждого положительного заряда всегда сопровождается появлением равного по абсолютному значению отрицательного заряда. Ни положительный, ни отрицательный заряд не могут исчезнуть в отдельности один от другого, они могут лишь взаимно нейтрализовать друг друга, если равны по абсолютному значению.

4)Релятивистская инвариантность заряда. В любой ИСО с какой бы скоростью она не двигалась заряд сохраняется.

5) Единица заряда в СИ – кулон (Кл). По определению, 1 кулон равен заряду, протекающему через поперечное сечение проводника за 1 с при силе тока 1 А.

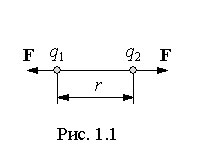
Сила взаимодействия зарядов - сила центральная, т. е. направлена вдоль прямой,соединяющей заряды (рис. 1.1). Для изотропной среды закон Кулона записывается следующим образом:

где k – коэффициент пропорциональности; q₁ и q₂ - величины взаимодействующих зарядов; r – расстояние между ними; r – радиус-вектор, проведенный от одного заряда к другому и направленный к тому из зарядов, на который действует сила.

Формулировка закона Кулона: «Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды отталкиваются, а разноименные притягиваются».

Следует отметить, что закон Кулона применим для расчета взаимодействия точечных зарядов и тел шарообразной формы при равномерном распределении заряда по их поверхности или объёму.

Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями до других тел, несущих электрический заряд.

Экспериментальные исследования показали, что при прочих равных условиях сила электростатического взаимодействия зависит от свойств среды, в которой находятся заряды. Поэтому коэффициент пропорциональности k в законе Кулона представляют в виде k = k₁ / e, где k₁ - коэффициент, зависящий только от выбора системы единиц; e - безразмерная величина, которая характеризует электрические свойства среды и называется относительной диэлектрическойпроницаемостью среды. Для вакуума e = 1.

В системе единиц СИ единица заряда кулон (Кл) определяется через единицу силы тока ампер (А) и единицу времени секунду (с), так что 1 Кл = 1 А×1 с. Коэффициент k₁ в этой системе определяется следующим образом: k₁ = 1 / 4pe₀ = 8,988×10⁹ (Н×м²) / Кл², где e₀ = 8,85×10^–12 Кл² / (Н×м²) и носит названиеэлектрической постоянной.

Таким образом, закон Кулона для изотропной и однородной среды записывается в виде

       (1.1)

Напряженность электрического поля

Заряды, находясь на некотором расстоянии один от другого, взаимодействуют. Это взаимодействие осуществляется посредством электрического поля. Наличие электрического поля можно обнаружить, помещая в различные точки пространства электрические заряды. Если на заряд в данной точке действует электрическая сила, то это означает, что в данной точке пространства существует электрическое поле. Силовой характеристикой электрического поля служит напряженностьE. Если на находящийся в некоторой точке заряд q₀ действует сила F, то напряженность электрического поля Е равна: Е=F/q₀. Графически силовые поля изображают силовыми линиями. Силовая линия – это линия, касательная в каждой точке которой совпадает с вектором напряженности электрического поля в этой точке.

Напряженность электрического поля – это физическая величина, численно равная силе, действующей на единичный заряд, помещенный в данную точку поля. За направление вектора напряженности принимают направление силы, действующей на точечный положительный заряд.

Однородное электрическое поле – это такое поле, во всех точках которого напряженность имеет одно и то же абсолютное значение и направление. Приблизительно однородным является электрическое поле между двумя разноименно заряженными металлическими пластинами. Силовые линии такого поля являются прямыми одинаковой густоты.

Если на заряд действуют одновременно несколько электрических полей, то напряженность поля равна векторной сумме напряженностей всех полей (принцип суперпозиции):

Индукция электрического поля. Напряженность электрического поля является силовой характеристикой поля и определяется не только зарядами, создающими поле, но зависит и от свойств среды, в которой находятся эти заряды.

Часто бывает удобно исследовать электрическое поле, рассматривая только заряды и их расположение в пространстве, не принимая во внимание свойств окружающей среды. Для этой цели используется векторная величина, которая называется электрической индукцией или электрическим смещением. Вектор электрической индукции D в однородной изотропной среде связан с вектором напряженности Е соотношением

.

Единицей измерения индукции электрического поля служит 1 Кл/ м². Направление вектора электрического смещения совпадает с вектором Е. Графическое изображение электрического поля можно построить с помощью линий электрической индукции по тем же правилам, что и для линий напряженности.Вычисление характеристик электрического поля во многих случаях сильно упрощается применением важной теоремы, излагаемой ниже.

Поток вектора напряженности электрического поля. Пусть небольшую площадку DS (рис.1.2) пересекают силовые линии электрического поля, направление которых составляет с нормалью n к этой площадке угол a. Полагая, что вектор напряженности Е не меняется в пределах площадки DS, определим поток вектора напряженности через площадку DS как

DF_E = E DS cos a.       (1.3)

Поскольку густота силовых линий равна численному значению напряжённости E, то количество силовых линий, пересекающих площадку DS, будет численно равно значению потока DF_E через поверхность DS. Представим правую часть выражения (1.3) как скалярное произведение векторов E и DS = n DS, где n – единичный вектор нормали к поверхности DS. Для элементарной площадки dS выражение (1.3) принимает вид

dF_E = E dS

Через всю площадку S поток вектора напряженности вычисляется как интеграл по поверхности

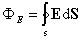
Поток вектора электрической индукции. Поток вектора электрической индукции определяется аналогично потоку вектора напряженности электрического поля

dF_D = D dS

В определениях потоков заметна некоторая неоднозначность, связанная с тем, что для каждой поверхности можно задать две нормали противоположного направления. Для замкнутой поверхности положительной считается внешняя нормаль.

Теорема Гаусса. Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхности S (рис. 1.3). Поток вектора индукции через элемент поверхности dS равен    (1.4)

Составляющую dS_D = dS cosa элемента поверхности dS в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиусаr, в центре которой расположен заряд q.

Учитывая, что dS_D / r² равен элементарному телесному углу dw, под которым из точки нахождения заряда q виден элемент поверхности dS, преобразуем выражение (1.4) к виду dF_D = qdw / 4p, откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4p, получим

F_D = q.

Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен заряду, заключенному внутри этой поверхности.

 Если произвольная замкнутая поверхность S не охватывает точечный заряд q (рис. 1.4), то, построив коническую поверхность с вершиной в точке нахождения заряда, разделим поверхность S на две части: S₁ и S₂. Поток вектора Dчерез поверхность S найдем как алгебраическую сумму потоков через поверхности S₁ и S₂:

.

Обе поверхности из точки нахождения заряда q видны под одним телесным угломw. Поэтому потоки равны

.

Поскольку при вычислении потока через замкнутую поверхность используетсявнешняя нормаль к поверхности, легко видеть, что поток Ф_1D < 0, тогда как поток Ф_2D > 0. Суммарный поток Ф_D = 0. Это означает, что поток вектора электрической индукции через замкнутую поверхность произвольной формы не зависит от зарядов, расположенных вне этой поверхности.

Если электрическое поле создаётся системой точечных зарядов q₁, q₂,¼, q_n, которая охватывается замкнутой поверхностью S, то, в соответствии с принципом суперпозиции, поток вектора индукции через эту поверхность определяется как сумма потоков, создаваемых каждым из зарядов. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:

     (1.5)

Следует отметить, что заряды q_i не обязательно должны быть точечными, необходимое условие - заряженная область должна полностью охватываться поверхностью. Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём dV имеет заряд  . В этом случае в правой части выражения (1.5) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:

    (1.6)

Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса:поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля:

 _.

Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Еще раз подчеркнем, что, несмотря на то, что напряжённость электрического поля E и электрическая индукция D зависят от расположения в пространстве всех зарядов, потоки этих векторов через произвольную замкнутую поверхность S определяются только теми зарядами, которые расположены внутри поверхности S.

Дифференциальная форма теоремы Гаусса. Отметим, что интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема Vна малые объемы V_i , получим выражение

справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом:

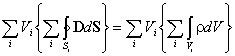     (1.7)

и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D):

Дивергенция вектора D в декартовых координатах:

Таким образом выражение (1.7) преобразуется к виду:

 _.

Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим

Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора D связана с плотностью заряда в той же точке равенством

или для вектора напряженности электростатического поля

.

Эти равенства выражают теорему Гаусса в дифференциальной форме.

Отметим, что в процессе перехода к дифференциальной форме теоремы Гаусса получается соотношение, которое имеет общий характер:

_.

Выражение называется формулой Гаусса - Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем.