9. Распределение Эрланга иногда называют усеченным распределением Пуассона. Необходимо вывести это распределение на примере рассмотрения модели m/m/s(0).

Статистическим равновесием называется вероятность устойчивого положения (равновесия). Известно, что устойчивое состояние существует, если имеет место единственная конечная вероятность распределения {P_r} такая, что при t   P_r (t)  P_r независимо от начальных условий.

Необходимо научиться строить диаграмму состояний переходов в модели M/M/s(0) и по ней получать уравнения локального и глобального баланса сети.

Необходимо рассмотреть модель M(n)/M/s(0), построить диаграмму состояний переходов и получить распределение Энгсета и биномиальное распределение; сравнить между собой различные распределения: ПуассонаЭрлангаЭнгсетаБиномиальное.

К показателям качества работы сети с коммутацией каналов следует отнести вероятность блокировки. В рамках степени обслуживания GOS различают вероятность перегрузки по вызовам, вероятность перегрузки по времени и к.п.д. линии или занятия. Необходимо вывести формулу потерь Энгсета и формулу потерь Эрланга (формула Эрланга B).

Общая коммутируемая нагрузка не зависит от пути линейного искания. Различают LTC (емкость последней линии) и ATC (емкость дополнительной линии). Параметры LTC и ATC используются при строительстве и оптимизации систем альтернативной маршрутизации.

10. Условием того, что устойчивого состояния в системе с запаздыванием не существует, является P₀ = 0, т.е. система перегружена и a  s. Это означает, что очередь со временем будет только бесконечно расти.

Фактор использования определяется из условия  = a / s и определяет коммутируемую нагрузку из расчета на одну линию (коммутационный прибор). Известно, что устойчивое состояние существует, если и только если  < 1.

Вероятность ожидания определяется как вероятность того, что сообщение будет ждать, обозначается как M(0), оценивает вероятность того, что время ожидания превышает 0, и рассчитывается по формуле Эрланга C.

Порядок обслуживания, такой как FIFO, RSO, LIFO и т.д., в котором ожидающие вызова обслуживаются, независимо от их сервисного времени, классифицируется как дисциплина обслуживания без последействия.

Порядок обслуживания, такой как SSTF (shortest service time first), зависит от сервисного времени, классифицируется как дисциплина обслуживания с последействием, для которой формула Литтла не имеет силы.

11. Стохастическим процессом называется целочисленная функция случайных переменных {N(t); t  0} с параметром t, говорят число вызовов, находящихся в системе во время t. Параметр t часто рассматривается как время и, если N(t) = j, то говорится, что процесс должен находится в состоянии j во время t. Если стохастический процесс обладает свойством марковости, то такой процесс называется Марковским процессом.

Процессом рождения-гибели называется Марковский процесс, в котором состояние перехода занимает только один шаг. При t0 процесс рождения-гибели описывается соотношением

(11)

где  – называется темпом рождения;

 – называется ритмом гибели, ₀ = 0.

Расширенная модель M(n)/M/s(m,) продуцирует в особых случаях все основные Марковские модели. Параметр  =  /  следует рассматривать как ту дополнительную нагрузку, которую формирует очередь. Следовательно, параметр  следует рассматривать как темп освобождения очереди (ритм депортации вызова из очереди для обслуживания на СМО).

Показателями качества функционирования расширенной Марковской модели являются время ожидания W, вероятность блокировки B, вероятность ожидания M(0) и функция дополнительного распределения времени ожидания (вероятность того, что время ожидания превысит t) M(t).

12. В модели транспортного переполнения Пуассоновский поток поступает с темпом  и если находит все сервера s первичной группы занятыми, то блокированный трафик перетекает во вторичную группу с бесконечным числом серверов. Необходимо ознакомиться с моделью, подробно изучить ее элементы, строить диаграмму состояний перехода для модели переполнения и по условию глобального баланса сети получать уравнения устойчивого состояния.

Вторичная группа бесконечна и процесс, происходящий в ней, характеризуется последовательностью вызовов переполнения. Характеристикой этой последовательности служит n-ый факториал момента M_n, который вычисляется по формуле Хеффиза. Промежутки времени между переполнениями пульсируют, LST (Лапласа-Стайлтьеса преобразования) которых задаются по формуле Десклоукса.

Математическое ожидание нагрузки от вызовов переполнения и ее дисперсия задаются по формуле Вилкинсона. При строительстве СМО требуется решение обратной задачи: необходимо определить нагрузку и неполнодоступный пучок линий по заданному математическому ожиданию и дисперсии переполненных вызовов. Для указанной цели применяют формулу Рэппа.

13. Метод случайного эквивалента – equivalent random theory (ERT) широко применяется при проектировании альтернативных систем маршрутизации. Здесь определяется единственным образом эквивалент случайной транспортной нагрузки a* и число фиктивных линий s* в первичном пучке. Отсюда и вычисляется искомая средняя вероятность блокировки переполненного направления. Однако средняя величина не обеспечивает индивидуальную вероятность блокировки для транспортных нагрузок a и a₁, соответственно, по высоко-используемому и альтернативному маршруту спроектированной схемы линейного резервирования.

Для оценок индивидуальных возможностей схемы линейного резервирования по направлениям переполненный процесс часто аппроксимируется прерывистым Пуассоновским процессом (IPP). Здесь Пуассоновский вход с темпом  прерывается случайным коммутатором с экспоненциальными on и of интервалами с величинами  ^–1 и ^–1, соответственно.

Процесс суперпозиции переполненного трафика и случайного фонового трафика в обходном маршруте не пульсирует. Однако при GI-аппроксимации процесс суперпозиции рассматривается как пульсирующий, и альтернативный маршрут моделируется как GI/M/s₁(0). Наконец, используя закон сохранения нагрузки и PASTA, мы определяем индивидуальные искомые вероятности блокировки.

14. Для оценки системы альтернативной маршрутизации в телефонных сетях используется так называемый условный метод. При этом стоимостная пропорция альтернативного маршрута к высоко-используемому k = ATC/LTC минимизирует систему оценок.

Оптимальное проектирование для минимизации стоимости системы по заданной вероятности блокировки B в обходном пути (пучок линий s₁) сводится к проблеме нелинейного программирования для минимизации целевой функции f = s+ks₁.

Схема линейного резервирования используется для защиты степени обслуживания GOS при разбалансировке индивидуальных вероятностей блокировки. При изучении структурной схемы линейного резервирования следует усвоить назначение составляющих элементов, обратить внимание на различия, связанные с видом приоритетов поступающих потоков ординарных и неординарных вызовов.

15. Составив систему уравнений устойчивого состояния для схемы линейного резервирования, мы сталкиваемся с трудностями при аналитическом решении в силу большого количества переменных. В таких случаях применяют численный анализ уравнений состояний.

На практике используется рекуррентный алгоритм с использованием начального веса вероятности

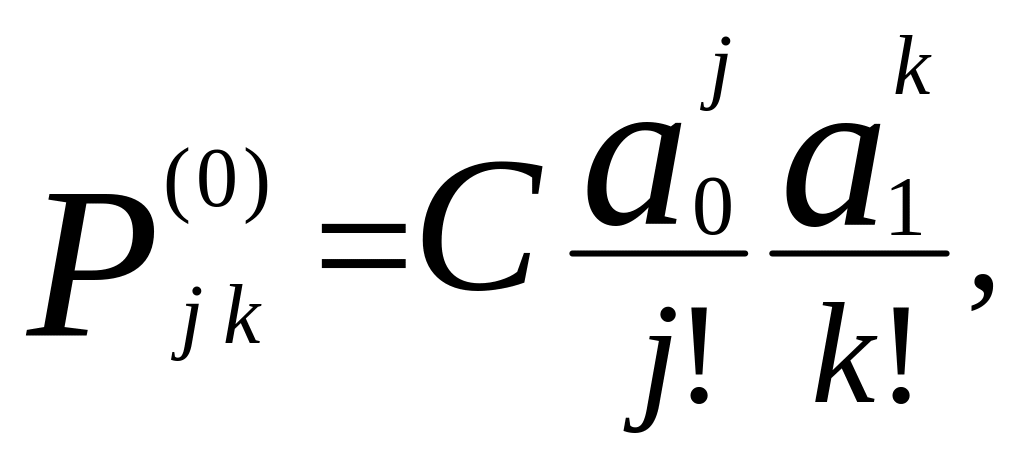(12)

где C – нормализирующая константа.

Последовательные вычисления продолжаются до тех пор, пока погрешность не снизится до предрешенной ошибки. В зависимости от значения вводимого весового фактора  алгоритм носит название итерация Гаусса-Шидела ( = 1) либо метод сверх-релаксации ( > 1).

16. Если время интервала Х между последовательными занятиями как достоверного события, говорят, вызов поступил, является независимым и идентично распределенным (iid) – independently and identically distributed – с функцией распределения F(x), процесс {X} называется пульсирующим процессом. Пуассоновский процесс является особым случаем пульсирующего процесса, в котором функция распределения F(x) экспоненциально распределена.

Для пульсирующего процесса (см. рис.9) интервал времени X*X от произвольно наблюдаемой точки X* до момента следующего занятия называется остаточным (жизни) временем или будущим временем повторения (вперед). В этой связи порожденный занятием интервал X называется временем жизни.

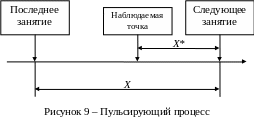
Время от последнего занятия до наблюдаемой точки эпохи называется веком или прошлым временем повторения (назад). Известно, что век, как и остаточное время X*, распределен согласно функции распределения

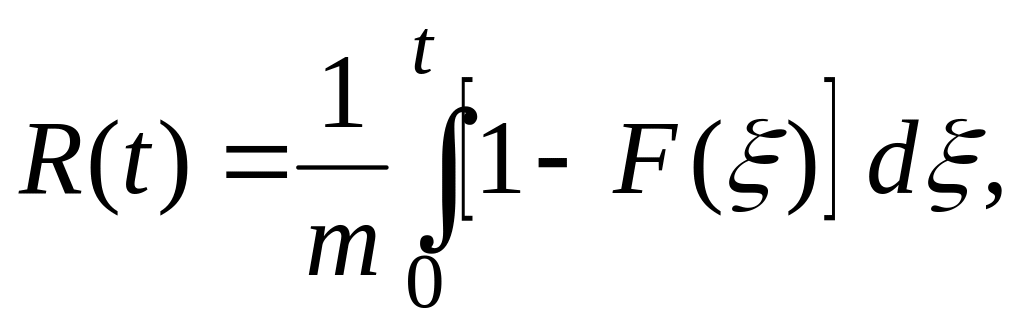(13)

где m = E{X} – есть математическое ожидание времени жизни X.

В основном полагают, что F(x) должна быть функцией распределения случайной непрерывной переменной Х  0. Тогда определяют Laplace-Stieltjes transform (LST) от F(x) как

(14)

где – является функцией плотности Х.

Преобразования LST функции распределения F(x) эквивалентно преобразованиям Лапласа (LT) функции плотности f(x). Преобразования LST распределения остаточного времени R(t) выражаются как

(15)

где f*(θ) – является LST времени жизни распределения F(x).

Отсюда получаем среднее остаточное время

(16)

где E{X ²} – является вторым моментом Х,

σ² – является дисперсией Х,

является квадратичным коэффициентом вариации (SCV).

Рассмотрим систему, в которой вызовы поступают в пульсирующий процесс с темпом , и потребуем экспоненциального времени обслуживания со средней величиной ^–1. Полагая, что P_j вероятность того, что j вызовов существует в системе в устойчивом состоянии, а П_j – вероятность как раз перед поступлением вызова, мы имеем закон сохранения темпа:

(17)

Для систем с потерями закон интерпретируется следующим образом. Обозначим состояние наличия в системе j вызовов символом S_j. Так как П_j–1 есть вероятность от состояния S_j–1 как раз перед поступлением вызова, а  есть темп поступления вызова, то левая сторона закона (17) представляет собой переход темпа от S_j–1  S_j. С другой стороны, так как j есть темп освобождения (ритм завершения) вызова, а P_j есть вероятность существования j вызовов, то правая сторона закона (17) представляет собой переход темпа от S_j  S_j–1. Таким образом, обе стороны балансируют в устойчивом состоянии, обеспечивая локальный баланс сети: rate-up = rate-down.

Та же самая интерпретация применяется и для систем с запаздыванием за исключением тех случаев, когда темп освобождения (ритм завершения) вызова принимает значение s при j >s, так как только s обслуживаемых вызовов могут завершаться.

17-18. Известно, что мультисервер систем с потерями и произвольным временем обслуживания M/G/s(0) эквивалентен Марковской модели M/M/s(0), и вероятность блокировки здесь задается формулой Эрланга В. Кроме того, вероятность блокировки для системы с ограниченным числом входов от n источников M(n)/G/s(0) задается потерями по формуле Энгсета. Данные свойства относятся к робастности сервисного времени.

Известно, что система M/G/1 имеет устойчивое состояние, если и только если предлагаемая транспортная нагрузка a =  = h < 1 erl, где h есть среднее время обслуживания, а  – коэффициент использования системы. Это может быть понято интуитивно, потому что сервер может обслужить 1 erl, как максимум.

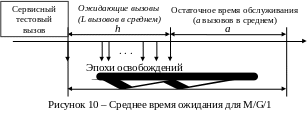
Выберем некоторый вызов и пометим его как тестовый вызов (см. рис.10). Вероятность того, что сервер занят, когда тестовый вызов поступит, по свойству 3 нагрузки и PASTA равна а. Время до тех пор, пока не завершится обслуживание вызова, является остаточным сервисным временем. Отсюда, обозначив среднее остаточное время обслуживания символом , среднее число ожидающих вызовов – , а среднее время ожидания – , мы имеем при порядке обслуживания вызовов FIFO следующую зависимость:

= a + h. (18)

С правой стороны выражения (18) первое произведение соответствует среднему времени для вызова в обслуживании, если некоторый должен быть завершен, а второе произведение соответствует обслуживанию тех ожидающих вызовов, которые стоят в очереди впереди тестового вызова.

Используя формулу Литтла =  и решая зависимость (18), мы получим среднее время ожидания

(19)

Из выражения (16) мы получим среднее остаточное время

(20)

где C_s² = σ_s²/ h² – является SCV сервисного времени (обслуживания);

σ_s²– является дисперсией сервисного времени (обслуживания).

Подставляя среднее остаточное время (20) в среднее время ожидания (19), мы получим формулу Полячека-Хинчина:

(21)

В стохастическом процессе момент времени, в котором свойство марковости держится, называется пульсирующей точкой. Для системы M/G/1 эпоха депортации (освобождения), в которой вызов завершается и покидает систему, становится пульсирующей точкой.

Марковский процесс с дискретным пространством состояний называется Марковской цепью. В Марковской цепи все времена эпох, в которых состояние изменяется, становятся пульсирующими точками. С другой стороны, стохастический процесс называется внедренной (вложенной) Марковской цепью, если пульсирующие точки внедряются или вкладываются в особое время эпох, таких как депортация (освобождение) вызова в системах типа M/G/1.

Во внедренной Марковской цепи (см. рис.11) состояние вероятности П_j* как раз после освобождения (депортации вызова) равно состоянию вероятности П_j как раз перед поступлением вызова в устойчивом состоянии. Из PASTA следует, что если в системе M/G/1 существует j вызовов, то P_j = П_j = П_j* .

Распределение времени ожидания W(t) в системе M/G/1 определяют по формуле Бенеша. Может быть показано, что уравнение интеграла Волтерра удовлетворяет распределению W(t). Для системы M/D/1 получено аналитическое выражение для функции распределения времени ожидания W(t), а для системы M/G/1(m) получена формула расчета среднего времени ожидания .

19-20. Известно, что в системе M/D/s существует устойчивое состояние, если и только если a < s.

Генерирующая функция g(z) от вероятности P_j определяется как

(22)

Среднее время ожидания рассчитывается по формуле Кроммелина-Полячека.

Функция распределения времени ожидания задается как

W(kh+x) =b(ks +s – 1), k = 0, 1, … ; 0 ≤ x < h, (23)

где b(ks +s – 1) – вероятность того, что ks +s – 1 существует в системе в интервале времени (t₀ + x). Она выводится из функции Q_r при t₀   .

Функция (23) задается следующим образом. Выберем произвольный вызов и пометим его как тестовый вызов. Предположим, что тестовый вызов поступает во время t₀ в устойчивом состоянии, а (ks +s – 1) вызовов существуют в интервале времени (t₀ + x). Так как s вызовов освобождают систему в течение каждого времени h (времени обслуживания), то по истечении времени kh число занятых серверов становится (s – 1). Затем вводится в обслуживание тестовый вызов.

Функция распределения времени ожидания однолинейной системы с постоянным временем обслуживания Пуассоновской нагрузки порта M/D/1 определяется как

W(t) = (1 – a) e^{ t} , 0 < t ≤ h. (24)

Среднее время ожидания в системе M/D/1вычисляется как

(25)

Необходимо отметить, среднее время ожидания в очереди (25) в два раза меньше, чем в системе M/M/1.

Таким образом, однолинейная система с постоянным временем обслуживания M/D/1 в два раза эффективнее в эксплуатации, чем однолинейная система с экспоненциальным сервером M/M/1.