Элементы теории множеств.

1. Логические символы

Квантор   - заменяет выражение "для любого", "для произвольного", "для какого бы ни было".

Квантор   - заменяет выражение "существует", "найдется".

Запись   (импликация) означает, что из справедливости высказывания A вытекает справедливость высказывания B. Если, кроме того, из справедливости высказывания B вытекает справедливость A, то записываем  . Если  , то высказывание B является необходимым и достаточным условием для того, чтобы выполнялось высказывание A.

Если предложения A и B справедливы одновременно, то записываем  . Если же справедливо хотя бы одно из предложений A или B, то записываем  .

2. Операции над множествами

Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит.

Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в виде A = {a, b, c, ...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:

                  N - множество всех натуральных чисел;                   Z - множество всех целых чисел;                   Q - множество всех рациональных чисел;                   R - множество всех действительных чисел;                   C - множество всех комплексных чисел;                   Z₀ - множество всех неотрицательных целых чисел.

Запись   (или  ) означает, что элемент a принадлежит множеству A.

2.СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ.

Веще́ственное, или действи́тельное число ^[1] — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений ^[2].

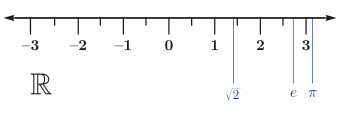
Числовая прямая

Если натуральные числа возникли в процессе счета, рациональные — из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.

Наглядно понятие вещественного числа можно представить себе при помощи числовой прямой. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять некоторое, и притом только одно, вещественное число. Вследствие этого соответствия термин числовая прямая обычно употребляется в качестве синонима множества вещественных чисел.

Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин (несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии — чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия^[3]. Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере была создана строгая теория вещественных чисел.

С точки зрения современной математики, множество вещественных чисел — непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле.

Множество вещественных чисел имеет стандартное обозначение — R («полужирное R»), или   (англ. blackboard bold «R») от лат. realis — действительный.

3.Прямая линия. уравнение прямой.

Пряма́я — одно из основных понятий геометрии.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где  ,   и   — произвольные постоянные, причем постоянные  и   не равны нулю одновременно.Вектор с координатами  называется нормальным вектором, он перпендикулярен прямой. Вектор с координатами (−B, A) или (B, −A) называется направляющим вектором.

При   прямая проходит через начало координат. Также уравнение можно переписать в виде

4.понятие от кривых вторго порядка

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов   отличен от нуля.

5.понятие функции.

Функция (отображение, оператор,преобразование) — математическое понятие, отражающее связь между элементамимножеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как однавеличина полностью определяет значение другой величины. Так значение переменной  однозначно определяет значение выражения  , а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

6.элементарные функции.

После введения в математическую деятельность понятия функции внимание математиков было обращено на изучение большого количества различных функциональных зависимостей. В результате непрерывного развития математики и в настоящее время появляются все новые классы функций.

Среди всего многообразия функций исторически выделились функции, отличающиеся своей простотой и наиболее широкой областью применения. Это так называемые простейшие элементарные функции, основное значение которых состоит в том, что они составляют базу для изучения более сложных функций, являясь в большинстве своем составными элементами последних.

Простейшими элементарными функциями обычно называют линейную (y=kx+b), квадратичную (y=ax²+bx+c), степенную (y=xⁿ, где n целое число, не равно 1), показательную (y=a^x,где a больше 0 и не равно 1), логарифмическую (y=log_a x, где aбольше 0 и не равно 1), тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x), обратные тригонометрические (y=arcsin x, y=arccos x, y=arctg x, y=arcctg x).

К элементарным функциям относятся основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения и деления) и суперпозиций.

Выделим классы функций, которые получены из элементарных:

1. Целая рациональная функция (или многочлен): y=a₀xⁿ+a₁x^n-1+...+a_n, где n - целое неотрицательное число (степень многочлена), a₀, a₁, ..., a_n - постоянные числа (коэффициенты).

2. Дробно-рациональная функция, которая является отношением двух целых рациональных функций.

Целые рациональные и дробно-рациональные образуют класс рациональных функций.

3. Иррациональная функция - это та, которая строится с помощью суперпозиции рациональной функции и степенных функций с рациональными показателями.

Рациональная и иррациональная функции образуют класс алгебраических функций. Алгебраическая функция - произвольная функция y=f(x), которая удовлетворяет уравнению:

A₀(x)yⁿ+A₁(x)y^n-1+...+A_n-1(x)y+A_n(x)=0.

Элементарные функции, которые не являются алгебраическими, называются трансцендентными.

7.пределы функции.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).

Предел фу́нкции — одно из основных понятий математического анализа.

8.бесконечно малые.