
Некоторые классы интегрируемых функций.
Определение:
Функция f(x)
называется равномерно непрерывной на
множестве {X},
если для любого ε>0
найдется δ>0
такое, что для любой пары чисел x’,
x’’
из
множества {X},
удовлетворяющих неравенству
 выполняется неравенство
выполняется неравенство
 (при этом δ=δ(ε)
и не зависит от x)
(при этом δ=δ(ε)
и не зависит от x)
Теорема 9: Непрерывная на сегменте [a, b] функция f(x) равномерно непрерывна на этом сегменте.
Следствие из теоремы 9: Пусть функция f(x) непрерывна на [a, b]. Тогда (в соответствие с ё равномерной непрерывностью) для любого ε>0 можно найти δ>0 такое, что на любом частичном сегменте [c, d], сходящемся в [a, b] и имеющем длину меньшую δ, колебание ω функции будет меньше ε.
Теорема 10: Непрерывная на сегменте [a, b] функция f(x) интегрируема на этом сегменте.
Доказательство:
Пусть дано произвольное ε>0.
Тогда в соответствии со следствием
из Т.9
для любого ε1=ε/(b-a),
найдется
δ>0
такое,
что на всех частичных сегментах разбиений
T,
длина которых меньше
δ, колебание
функции будет меньше ε1.
Оценим
S-s:
 (
( )
)
S-s<ε – необходимое и достаточное условие интегрир. выполняется.
Теорема 11: Ограниченная на сегменте [a, b] функция f(x), имеющая конечное число точек разрыва, интегрируема на этом сегменте.
Теорема 12: Ограниченная монотонная на сегменте [a, b] функция интегрируема на этом сегменте.
Доказательство:
(проведем для неубывающей функции) Пусть
выбрано произвольное ε>0.
Зададим
разбиение сегмента [a,
b]
на равные по длине частичные сегменты,
длина которых меньше δ=
ε/f(b)-f(a).
Оценим
S-s:
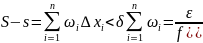 ,
(
,
( ),
S-s<ε
),
S-s<ε
Несобственный
интеграл 1 рода: Определение:
Пусть функция f(x)
интегрируема на любом сегменте [a;b],
тогда несобственным интегралом 1-го
рода
 называется предел
называется предел
 .
Несобственный интеграл называется
сходящимся,
если существует конечный предел
.
Несобственный интеграл называется
сходящимся,
если существует конечный предел
Теорема
13 (Критерий Коши):
Для
сходимости несобственного интеграла
необходимо и достаточно, чтобы для
любого ε≥0 нашлось число A≥0,
такое, что для любых R’
и R”,
удовлетворяющих условию R’>A
и R’’>A
выполняется неравенство | |< ε
|< ε
Теорема
14 (Общий признак сравнения):
Пусть
на множестве a≤x≤∞выполняется
неравенство |f(x)|≤|g(x)|,
тогда из сходимости интеграла
 следует сходимость интеграла
следует сходимость интеграла
Теорема
15 (Частный признак сравнения):
Пусть на множестве a≤x≤∞выполняется
неравенство |f(x)|≤с/xa
и a>1.
Тогда интеграл
сходится. Если a<1
– интеграл расходится. Следствие:
Пусть при x→∞
модулю ф-ии f(x)
имеет порядок 1/xa,
т. е. f(x)
 1/xa.
Тогда при a>1
интеграл сходится, а при a<1
– расходится.
1/xa.
Тогда при a>1
интеграл сходится, а при a<1
– расходится.
Абсолютно
и условно сходящийся интеграл:
Несобственный
интеграл
называется абсолютно сходящимся, если
сходится интеграл
 .
Несобственный интеграл называется
условно сходящимся, если он сходится,
а
расходится.
.
Несобственный интеграл называется
условно сходящимся, если он сходится,
а
расходится.
Теорема
16 (Признак Дирихле-Абеле):
Пусть в несобственном интеграле
 функция f(x)
имеет граничную первообразную F(x)
на множестве [a;
+∞), a
ф-ия g(x)
немонотонно не возрастая стремится к
0 при x→∞
и имеет непрерывную производную на
мн-ве [a;
+∞). Тогда несобственный интеграл
сходится.
функция f(x)
имеет граничную первообразную F(x)
на множестве [a;
+∞), a
ф-ия g(x)
немонотонно не возрастая стремится к
0 при x→∞
и имеет непрерывную производную на
мн-ве [a;
+∞). Тогда несобственный интеграл
сходится.
Замена
перем-ой и интегрирование по частям для
несобств. интегралов. Пусть
выполняются следующие условия: 1)ф-ия
f(x)
непрерывна на полупрямой a≤x≤∞
2) множество [a;∞)
является множеством значений для
некоторой ф-ии x=g(t)
определенной мн-ве d≤t≤∞
ф-ия
g(t)
является строго монотонной и имеет
производную. 3) g(d)=a.
Тогда из сходимости одного из интегралов
и
 следует сходимость другого и их равенство.
следует сходимость другого и их равенство.
Пусть
ф-ии U(x)
и V(x)
имеют непрерывные производные на мн-ве
[a;
+∞) Пусть кроме того произведение функций
ограничено на этом мн-ве. Тогда из
сходимости одного из интегралов
 и
и
 следует сходимость другого и выполняется
равенство:
=U(x)V(x)-
следует сходимость другого и выполняется
равенство:
=U(x)V(x)-
Несобственный
интеграл 2 рода: Понятие
несобственного интеграла 2 рода вводится
если нарушается условие ограниченности
ф-ии в области интегрирования. Т. е.
функция имеет особые точки. Точка x=b
называется особой точкой данной ф-ии,
заданной на промежутке [a;b),
если f(x)
не ограничена на [a;b),
и является ограниченной на любом сегменте
[a;b-µ),
содержащимся в [a;b).
Несобственным интегралом 2 рода для
ф-ии
для ф-ии f(x)
с особой точкой x=b
называется предел

Теорема
17 (критерий Коши):
Для
сходимости несобственного интеграла
2 рода от ф-ии f(x)
с особой точкой x=b,
необходимо и достаточно, чтобы для
любого ε≥0 нашлось ð>0, такое, что для
любой пары чисел µ’ и µ”, удовлетворяющих
неравенству 0≤µ’≤µ’’≤ð выполнялось
равенство: | |< ε
|< ε
Возможность
сведения несобственного интеграла 2
рода… Пусть
ф-ия f(x)
на [a;b)и
x=b
– особая точка. Пусть f(x)
интегрируема на любом сегменте [a;b-µ),
содержащимся в [a;b).
Рассмотрим интеграл
 .
Сделаем замену x=b-1\t
Тогда dx=(1/t2)dt
t=
1/(b-x)
t1=1/(b-a)
t2=1/µ.
Получим:
=
.
Сделаем замену x=b-1\t
Тогда dx=(1/t2)dt
t=
1/(b-x)
t1=1/(b-a)
t2=1/µ.
Получим:
= )
По определению несобственного интеграла
2 рода это
)
По определению несобственного интеграла
2 рода это
 =
=
 – несбственный интеграл 1 рода.
– несбственный интеграл 1 рода.
Несобственный
интеграл в в смысле главного значения
Несобственным
интегралом первого рода в смысле главного
значения
 называется
предел
называется
предел
 .
Несобственным интегралом втрого рода
в смысле главного значения
от ф-ии f(x)
с особой точкой x=с
называется предел
.
Несобственным интегралом втрого рода
в смысле главного значения
от ф-ии f(x)
с особой точкой x=с
называется предел
 +
+ }
}
Координатное
и Евклидово пространство:
Определение:
Множество всевозможных упорядоченных
совокупностей x1,x2,…,xm,
составленных из вещественных чисел,
называется m-мерным
координатным пространством.
Определение:
Координатное пространство называется
m-мерным
Евклидовым
пространством Em,
если для любой пары точек M’(x’1,x’2,…,x’m)
и M’’(x’’1,x’’2,…,x’’m)
можно ввести понятие расстояние ρ(M’,M’’)
между этими точками, которое определяется
формулой: ρ(M’,M’’)=
