
Понятие первообразной и неопределенного интеграла: Определение: Функция F(x) называется первообразной для функции f(x) на интервале (a;b) если F(x) дифференцируема в любой точке (a;b) и F’(x)=f(x) для любого x € (a;b).Определение: Совокупность всех первообразных для функции f(x) на интервале (a;b) называется неопределенным интегралом от функции f(x) и обозначается символом ∫f(x)dx. ∫f(x)dx=F(x)+c.
Свойства: 1) (∫f(x)dx)’=f(x) 2)∫F’(x)dx=F(x)+c 3)∫kf(x)dx=k∫f(x)dx 4) ∫(f1(x)+f2(x))dx=∫f1(x)dx+∫f2(x)dx 5) если ∫f(x)dx=F(x)+c и u=ϕ(x)- непрерывно дифференцируемая функция на (a;b), то ∫f(u)du=F(u)+c
Таблица неопределенных интегралов: 1)∫xadx=xa+1/a+c 2) ∫dx/x=ln|x|+с 3) ∫axdx=ax/ln a +c
4)∫sin(x)dx=-cos(x)+с
5)∫cos(x)=sin(x)+c 6) ∫dx/cos2x=tg(x)+c
7) ∫dx/sin2x=-ctg(x)+c
8)∫dx/(x2+a2)=(1/a)arctg(x/a)+c
9)∫dx/(a2-x2)=(1/2a)ln|(a+x/(a-x)|+c
10)∫dx/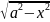 =arcsin(x/a)+c
11)∫dx/
=arcsin(x/a)+c
11)∫dx/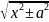 =ln
|x+
|+с
12) ∫sh(x)dx= chx+c.
=ln
|x+
|+с
12) ∫sh(x)dx= chx+c.
Основные методы вычисления неопределенных интегралов: Метод замены переменной: ∫f(x)dx=|t=ф(x) x=ф-1(t) dx=(ф-1)’dt|=f(ф-1 (t)) (ф-1)’dt. Интегрирование по частям: пусть ф-ии u(x) и V(x) дифференцируемы на интервале (a;b). Имеет место формула ∫UV’dx=UV-∫U’Vdx или ∫UdV=UV-∫VdU. Имеются 3 группы: 1 группа: например ∫ ln x dx. За U=ln, arcsin x, arctg x…; dV=dx; 2 группа: например ∫(x2-1)cos x dx. за U – (x2-1), за dV – все стальное (cos x dx). 3 группа: ∫eaxsin(bx) dx за U=sin(bx) dV=eaxdx.
Интегрирование
рациональной дроби:
Определение:
Рациональная дробь – выражение вида
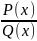 , где P(X)
и Q(x)
– алгебраические многочлены соответственно
m-го
и n-го
порядка. Дробь называется правильной,
если степень многочлена в числителе
меньше чем степень многочлена в
знаменателе. (m<n).
, где P(X)
и Q(x)
– алгебраические многочлены соответственно
m-го
и n-го
порядка. Дробь называется правильной,
если степень многочлена в числителе
меньше чем степень многочлена в
знаменателе. (m<n).
Теорема 1: Любой многочлен f(x) ненулевого порядка делится (без остатка) на комплекс ф(x)=x-а тогда и только тогда, когда число а является корнем многочлена f(x). Доказательство: поделим f(x) на ф(x) и запишем результат в виде: f(x)=ф(x)g(x)+r(x)=(x-a)g(x)+r(x). Поскольку ф(x) – многочлен 1 порядка, то r(x) – многочлен 0 порядка, т. е. γ(x)= c. f(x)=(x-a)g(x)+с. Для деления f(x) на ф(x) без остатка необходимо чтобы с=0. Подставим x=a. тогда f(a)=c. т. о. c=0, если а – корень многочлена f(x)=(x-a)g(x).
Теорема
2:
Пусть
- правильная рациональная дробь и
знаменатель этой дроби имеет вид
Q(x)=(x-x1)a1(x-x2)a2…(x-xk)ak(x2-p1x-q1)b1...(x2+plx+ql)bl
тогда эту дробь можно представить в
виде следующей алгебраической суммы
простых дробей:
=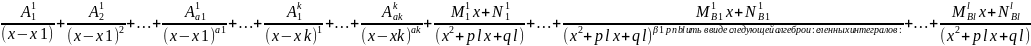 .
4
типа интегралов от рац. дробей:1:
∫
.
4
типа интегралов от рац. дробей:1:
∫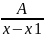 dx=Aln|x-x1|2:
∫
dx=Aln|x-x1|2:
∫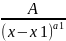 dx=A∫(x-x1)a1d(x-x1)=
dx=A∫(x-x1)a1d(x-x1)=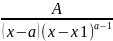 3:
3: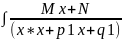 dx=
dx=
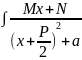 =|
=|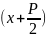 =t
dx=dt|=M
=t
dx=dt|=M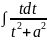 +(N-
+(N-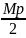 )
) =(M/2)ln(x2+px+q)+(
N-
)(1/a)arctg((x+p/2)/a)
4:
=(M/2)ln(x2+px+q)+(
N-
)(1/a)arctg((x+p/2)/a)
4: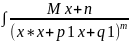 =|
=t
dx=dt|=
M
=|
=t
dx=dt|=
M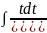 +(N-
)
+(N-
)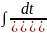 – рекурсивная формула.
– рекурсивная формула.
Интегрирование рациональной ф-ии от тригонометрической ф-ии: ∫R(sin x, cos x)dx сводится к интегралу от рациональной дроби с помощью 3 подстановок: 1- универсальная: t=tg(x/2) ∫R(sin x, cos x)dx= |t=tg(x\2) x=2arctg(t) dx=2dt\(1-t2) sin(x)=2t/(1+t2) cos(x)=(1-t2)/(1+t2)|=… 2 подстановка: выполняется если эта функция является нечётной относительно одного из элементов a) если R(-U,V)=R(U,V) ∫R(sin x, cos x)dx=∫R1(sin2 x, cos x)sin(x)dx=|cos(x)=t –sin(x)dx=dt|=∫R1(1-t2, t)= ∫R2(t)dt. Если (R(U,-V)=R(U,V), то t=sin(x) 3 подстановка: R(-U,-V)=R(U,V) ∫R(sin x, cos x)dx=∫R2(sin(x)/cos(x),cos2(x)dx=|t=tgx, dx=dt/(1+t2), cos2(x)=1/(1+t2)|=…
Интегрирование дробно-линейных ирр-ей: ∫R(x,(ax+b/cx+d)r1…(ax+b/cx+d)rk), где r1, r2, rk – рациональные числа, т. е. их можно представить: r1=m1/n1; r2=m2/n2, где n1, m1… - целые числа. Пусть n – общий знаменатель m1/n1, m2/n2… тогда эти дроби можно представить в виде r1=p1/n; r2=p2/n..сделаем замену (ax+b/cx+d)1\n=t ∫R(x,(ax+b/cx+d)r1…(ax+b/cx+d)rk)=| (ax+b/cx+d)1\n=t (ax+b/cx+d)=tn|=∫R((dtn-b/a-ctn), tp1, tp2, tpk) (dtn-b/a-ctn)’dt=∫R1(t)dt.
Интегрирование рационального бинома: Бином – xm(a+bxn)p 1 случай:p-целое x=ts s – наим. общее кратное дробей m и n. 2 случай: (m+1)/n – целое a+bxn=ts s – знаменатель p. 3 случай: (m+1)/n+1 – целое
ax-n+b= ts s- знаменатель p.
Специальные подстановки:
1)∫R(x,
)dx=|x=asint,dx=acos(t)dt, |=∫R(asin(t),
|=∫R(asin(t),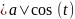 )cos(t)dt=∫R1(sint,cost)dt
2)∫R(x,
)cos(t)dt=∫R1(sint,cost)dt
2)∫R(x, )=|x=ash(t)
dx=ach(t)dt
=|a|ch(t)|=
…
)=|x=ash(t)
dx=ach(t)dt
=|a|ch(t)|=
…
3)
∫R(x, =|x=acht
dx=|a|sh(t)dt
=|a|sh(t)|=…
=|x=acht
dx=|a|sh(t)dt
=|a|sh(t)|=…
Определенный интеграл. Введём понятие определенного интеграла исходя из классической геометрической задачи вычисления площади криволинейной трапеции. Пусть функция g=f(x) определена на [a, b]. Определение: Ф-ия f(x) называется интегрируемой на сегменте [a,b], если существует конечный предел I интегральных сумм этой фу-ии при ∆->0.Число I называется определенным интегралом функции f(x).
Интегральные
суммы: Определение:
Величину I(xi,
ξ
i)
определенную
выражением
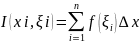 будем называть интегральной суммой
функции f(x),
соответствующей
данному T-разбиению
и данному выбору промежуточных точек
ξ
будем называть интегральной суммой
функции f(x),
соответствующей
данному T-разбиению
и данному выбору промежуточных точек
ξ
 [xi-1,
xi].
Введём
обозначения ∆=max
∆xi.
[xi-1,
xi].
Введём
обозначения ∆=max
∆xi.
Основные свойства определенного интеграла (6 свойств):
1.
Принять, что
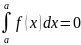
2.
При b>a
выполняется
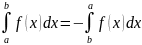
3.
Пусть функции f(x)
и g(x)
интегрируемы на сегменте [a,
b].
Тогда функции f(x)±g(x),
f(x)·g(x),
так
же интегрируемы на [a,
b].
При
этом для алгебраической суммы справедливо
равенство:
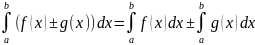
4.
Пусть функция f(x)
интегрируема
на [a,
b].
Тогда
и функция C·f(x)
(где С - постоянная) интегрируема
на
[a,
b].
Тогда
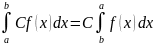
5. Пусть функция f(x) интегрируема на [a, b]. Тогда эта функция интегрируема на любом сегменте [c, d], содержащемся в [a, b].
6.
Пусть функция f(x)
интегрируема
на сегменте [a,
c]
и [c,
b].
Тогда она интегрируема на сегменте [a,
b].
При
этом справедливо равенство:
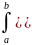 .
.
Три оценки определенных интегралов.
1я.
Пусть функция f(x)
интегрируема
и неотрицательна на сегменте [a,
b],
т.е. f(x)≥0
при
x
[a,
b].
Тогда
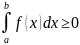
2я.
Пусть функции f(x)
и g(x)
интегрируемы на [a,
b]
и
пусть на [a,
b]выполняется
неравенство: f(x)≥g(x).
Тогда
Справедливо неравенство:
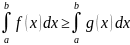
3я.
Пусть функции f(x)
и g(x)
интегрируемы на [a,
b]
и
пусть на [a,
b]выполняется
неравенство: g(x)≥0.
Пусть
кроме того числа m,
M
– точные нижние и верхние грани f(x)
на [a,
b].
Тогда
справедливы следующие неравенства:
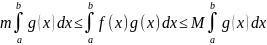 Доказательство:
В соответствии с определением m
и
M
должно выполняться: m≤f(x)≤M
на
[a,
b].
Умножим
эти неравенства на g(x).
Доказательство:
В соответствии с определением m
и
M
должно выполняться: m≤f(x)≤M
на
[a,
b].
Умножим
эти неравенства на g(x).
m g(x)≤f(x) g(x)≤M g(x) --->
Теорема
3(Формулы среднего значения):
Пусть функция f(x)
интегрируема
на [a,
b]
и
пусть m,
M
точки
нижняя и верхняя грани f(x)
на
[a,
b].
Тогда найдется такое число μ,
удовлетворяющее неравенствам: m≤μ≤M,
что выполняется следующее соотношение
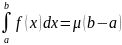 Доказательство:
Используем 3 оценку для случая g(x)=1.
,
Доказательство:
Используем 3 оценку для случая g(x)=1.
,
 .
Положим
.
Положим
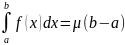 Тогда
Тогда
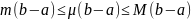 ,
m≤μ≤M.
,
m≤μ≤M.
Если
f(x)
непрерывная
на [a,
b]
функция,
то на сегменте [a,
b]
найдется точка ξ такая, что f(ξ)=μ.
Тогда
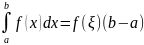 ,
где ξ
[a,
b].
,
где ξ
[a,
b].
Теорема
4:
Пусть функции f(x)
и g(x)
интегрируемы на [a,
b]
и
g(x)≥0.
Пусть
кроме того f(x)
непрерывна
на [a,
b].
Тогда
справедлива формула:
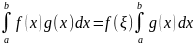 ,
где ξ
[a,
b].
,
где ξ
[a,
b].
Определенный
интеграл с переменным верхним пределом.
Пусть
функция f(x)
интегрируема
на сегменте, содержащемся в интервале
(a,
b).
Выберем
произвольную точку c
(a,
b)
и
точку x
(a,
b).
Тогда
имеет смысл функция:
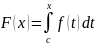 .
Определение:
Функция
.
Определение:
Функция
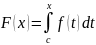 называется определенным интегралом с
переменным верхним пределом.
называется определенным интегралом с
переменным верхним пределом.
Теорема 5: Любая непрерывная на (a, b) функция f(x) имеет первообразную на этом интервале, одной из которых является функция , где x (a, b).
Доказательство:
Докажем, что функция
 дифференцируема. По определению
дифференцируема. По определению
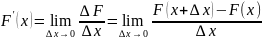 =
(пояснения:
=
(пояснения:
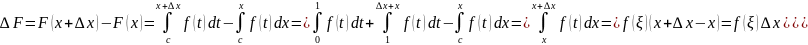 ,
где ξ
(x,
x+∆x).)=
,
где ξ
(x,
x+∆x).)= .
Т.о.
функция
является первообразной для f(x).
.
Т.о.
функция
является первообразной для f(x).
Формула
Ньютона-Лейбница. Пусть
f(x)
непрерывна
на [a,
b].
Тогда функция
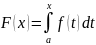 является первообразной для f(x).
Все
наборы первообразных это: Ф(x)=F(x)+C=
является первообразной для f(x).
Все
наборы первообразных это: Ф(x)=F(x)+C= Ф(a)=
Ф(a)=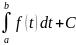 ,
b=ф(x),
Ф(x)=
,
b=ф(x),
Ф(x)=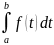 +ф(a)
+ф(a)
Если
x=b,
то
Ф(b)=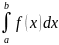 +ф(a),
т.о.
+ф(a),
т.о.
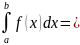 Ф(b)-Ф(a)=Ф(x)
Ф(b)-Ф(a)=Ф(x)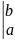 – формула
Н-Л.
– формула
Н-Л.
