1.Задачи и методы сопротивления материалов. Классификация нагрузок и расчетных схем. Метод сечений. Внутренние силовые факторы. Эпюры внутренних силовых факторов.

Общие понятия.

Возведение сооружений и строительство машин (которые далее будем называть конструкциями) начинается с составления проекта, в котором определяют форму, размеры и материал конструкции. Каждая конструкция составляется из отдельных деталей, взаимно соединенных между собой. Эти детали будем называть элементами конструкций. В процессе эксплуатации элементы в той или иной степени участвуют в работе и подвергаются действию различных внешних факторов: нагрузок, изменений температуры.

Под влиянием внешних сил элементы конструкций изменяют свою первоначальную геометрическую форму, объем и размеры. Такое изменение называют деформацией.

Величина деформации может при определенных условиях нарушить нормальную работу конструкции и даже оказаться опасной для целости того или иного элемента.

Для обеспечения нормальной и безопасной работы конструкция должна удовлетворять условиям прочности, жесткости и надежности.

Прочность – это способность конструкции выдерживать заданную нагрузку, не разрушаясь.

Жесткость – способность конструкции под действием внешних сил сопротивляться возникновению деформации.

Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.

Этими вопросами и занимается наука сопротивление материалов.

Сопротивление материалов – наука, в которой изложены принципы и методы расчета элементов конструкций на прочность, жесткость и надежность.

Кроме этих требований, проектируемые сооружения должны удовлетворять требованиям наибольшей экономичности и долговечности.

Классификация сил (нагрузок)

Деформирование элементов конструкции происходит под действием на них внешних сил. Равновесную систему внешних сил (состоит из активных и реакций связей), называют нагрузкой.  Нагрузки классифицируют:  - по способу приложения нагрузки к элементу конструкции - по характеру действия нагрузки на элемент конструкции По способу приложения нагрузки делят на поверхностные и объемные. Поверхностные силы (их разделяют на распределенные и сосредоточенные) действуют на участках поверхности тела (силы контактного взаимодействия тел, силы воздействия среды). Объемные силы распределены по всему объему тела, приложены к каждой его частице (это силы тяжести, магнитные силы, силы инерции) По характеру действия на тело нагрузки подразделяют на статические, циклические (повторно-переменные) и динамические (ударные) Статические нагрузки - постепенно возрастают от нуля до определенного значения, а затем не изменяются либо слабо изменяются с течением времени. Циклические нагрузки - изменяются во времени по какому-либо периодическому закону. Динамические нагрузки - нагрузки, прикладываемые внезапно.

При моделировании нагрузки вводятся понятия сосредоточенной силы (P или F, Н) и момента (момент M - пара сил, Нхм), распределенной нагрузки (q, Н/м).

Типы связи. Шарнирно-подвижная опора, шарнирно-неподвижная опора, жесткая заделка

Рассмотрим несколько типов связи: Шарнирно-подвижная опора Шарнирно-неподвижная опора Жесткая заделка Шарнирно-подвижная опора (каток) накладывает одну связь. Шарнирно-неподвижная опора - запрещает линейные перемещения. Жесткая заделка - запрещает линейные и угловые перемещения.

Классификацию расчетных схем должны и так знать

МЕТОД СЕЧЕНИЙ (РОЗУ)

Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию, чтобы внутренние силы стали явными.

Например для стержня можно применить прием мысленного рассечения на две части плоскостью, перпендикулярной продольной оси. Затем отбросить одну из полученных частей, что позволяет превратить внутренние силы, для целого стержня, во внешние для оставленной части стержня (рис.1.5).

Рис. 1.5

Силы взаимодействия будут в каждой точке проведенного сечения (рис. 1.6).

Рис. 1.6

Эту систему большого числа сил по правилам теоретической механики можно привести к одной точке (центру тяжести поперечного сечения), в результате чего получим главный вектор R и главный момент М (рис. 1.7).

2. Отбрасываем одну часть

Рис. 1.7

Теперь спроектируем   на три оси (продольную z и две взаимно-перпендикулярные поперечные х и у). В результате получим шесть внутренних силовых факторов: три силы N, Qx Qy и три момента Мx, My и Мz

Сила N называется продольной силой, силы Qx и Qy - поперечные силы. Момент относительно оси z - Мz - крутящий момент; и моменты Мx, My относительно поперечных осей - изгибающие.

Каждому из внутренних усилий соответствует определенный вид деформации (изменение формы), бруса. Например, продопьной силе N соответствует растяжение (или сжатие) бруса.

3. Заменяем

Рис. 1.8

Таким образом, рассматривается одна из полученных при рассечении частей стержня, которая нагружена приложенными к этой части внешними силами и шестью внутренними усилиями (рис. 1.8).

4. Уравновешиваем

Для установления связи внутренних и внешних сил можно к этой части применить уравнения равновесия, (уравновешиваем), так как известно, что если тело находится в целом в равновесии, то в равновесии и любая его часть.

Рассмотрим, например, уравнение  . Из внутренних усилий на ось z проектируется только продольная сила N.

Тогда

где  - проекция всех внешних сил, действующих на оставленную часть стержня, на ось z.

Отсюда вытекает следующее определение: продольная сила N численно равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону (рассматриваемую) от проведенного сечения.

Аналогичные определения для Qx, Qy , Мx, My и Mz. По первым буквам выполняемых операций (рассекаем, отбрасываем, заменяем и уравновешиваем) метод сечений иногда называют методом РОЗУ.

Под влиянием внешей нагрузки реальные тела деформируются, в отличие от абсолютно твердого тела, изучаемого в курсе теоретической механики. При этом между рядом раположенными частицами тела воникают, по законам физики, внутренние силы. Если мысленно рассечь деформированный брус плоским перечным сечением на две части и привести внутренние силы, действующие со стороны одной части на другую - к центру тяжести (площади) поперечного сечения, получим ГЛАВНЫЙ ВЕКТОР R и ГЛАВНЫЙ МОМЕНТ M системы этих внутренних сил. Эти величины (R и M) имеют такой смысл: Если мысленно заменить внутренние силы, действующие в сечении, силой R и моментом (парой сил) M (приложив их в центре тяжести поперечного сечения), то равновесие отсеченной части тела не нарушится. То есть R и M (совместно) являются статическим эквивалентом системы внутренних сил, действующих в сечении.  

Рис. 1,2,3: Внутренние силовые факторы (ВСФ) в поперечном сечении бруса

Проекции главного вектора R и главного момента M на ГЛАВНЫЕ ЦЕНТРАЛЬНЫЕ ОСИ поперечного сечения и ПРОДОЛЬНУЮ ось бруса называются ВНУТРЕННИМИ СИЛОВЫМИ ФАКТОРАМИ (ВСФ) в поперечном сечении.   ВСФ (см рис 1) обозначаются: 

• Проекция R на ось Z т е N называется продольной силой.

• Проекция R на ось Y т е Q_Y называется поперечной силой.

• Проекция R на ось X т е Q_X тоже называется поперечной силой.

• Проекция M на ось Z т е M_Z называется крутящим моментом.

• Проекция M на ось Y т е M_Y называется изгибающим моментом (в горизонтальной плоскости XZ ).

• Проекция M на ось X т е M_X тоже называется изгибающим моментом (в вертикальной плоскости YZ ).

Примечание: Существует два способа изображения пары сил: 1. В виде вектора - как показано на рис. 2 2. В виде пары сил. Чтобы перейти от одного способа к другому применяется ПРАВИЛО БУРАВЧИКА (см рис 3)

(Пример вычисления величины ВСФ и построения эпюр см здесь)

Знаки ВСФ. Дифференциальные зависимости при изгибе.

В качестве иллюстрации понятия "внутренние силовые факторы" рассмотрим пример - балку, к которой приложена нагрузка, действующая в вертикальной плоскости (плоскость YZ - см рис 1,2, 4.1). Так как продольная ось Z балки и внешняя нагрузка q находятся в одной плоскости (YZ) и реакции опор A и B - Y_A, Y_B - в этой же плоскости, то задача является плоской и можно изобразить расчетную схему в плоскости рисунка (см рис 4.2, 4.3, 4.4).  Выделим двумя бесконечно близкими друг к другу (расстояние dz) поперечными сечениямим тонкий элемент балки (см 4.1, 4.2, 4.3, 4.4) и рассмотрим его равновесие под действием ВСЕХ приложенных к нему внешних сил.

• Имеется в виду, что мы мысленно вырезали элемент из балки, заменив действие внутренних сил, действовавших со стороны левой и правой отброшенных частей статическими эквивалентами - внутренними силовыми факторами (Q,M - слева, Q+dQ, M+dM - справа.)

• Поэтому равновесие этого элемента (если оно было) - не нарушится. Но было ли равновесие? Конечно, потому что в сопротивлении материалов рассматриваются, как правило, неподвижные (покоящиеся) конструкции и их элементы. Из курса теоретической механики известно, что если тело находится в состоянии покоя (или равномерного прямолинейного движения относительно инерциальной системы координат) то система внешних сил, приложенных к этому телу, взаимно уравновешена.

• Обратите внимание, что ВСФ, приложенные к левой и правой границам отсекаемого элемента ВЗАИМНО ПРОТИВОПОЛОЖНЫ по направлению. Поэтому никак не возможно для ВСФ - поперечной силы Q и изгибающего момента M принять правила знаков + - , установленные в статике для сосредоточенных сил и пар сил. Правила знаков для ВСФ рассмотрим позже. Естественно, что в общем случае мы допускаем возможность изменения Q и M, поэтому к правой границе элемента прикладываем ВСФ: Q+dQ и M+dM. Остальные ВСФ (если они есть) не рассматриваем, так как они не входят в уравнения равновесия, которые будут рассмотрены.

• Рассмотрим уравнения равновесия отсеченного элемента с целью получить зависимости между q, Q и M (см рис 4.4). 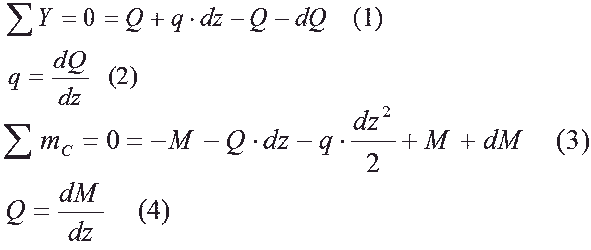 Формула (2) получена из ф. (1), а формула (4) - из ф. (3) - с учетом того, что dz² - бесконечно малая величина более высокого порядка, чем dz и может быть удалена.

Знаки ВСФ

В сопротивлении материалов принято следующее ПРАВИЛО ЗНАКОВ для ВСФ.:

• Продольная сила N считается положительной, если она направлена в сторону ВНЕШНЕЙ нормали к сечению, то есть РАСТЯГИВАЕТ элемент, показанный на рис 4.4 и отрицательной, если она СЖИМАЕТ элемент.

• Поперечная сила Q_Y (при расчете балок и плоских рам она обычно обозначается просто Q) считается положительной, если она направлена в сторону внешней нормали к сечению, ПОВЕРНУТОЙ на 90^o ПО ЧАСОВОЙ СТРЕЛКЕ.

• Изгибающий момент M_X считается положительным (для БАЛОК и горизонтальных участков РАМ), если он деформирует продольную ось бруса выпуклостью вниз (т е сжатые продольные "волокна" расположены сверху, а растянутые - снизу - см рис 5). В противном случае (выпуклостью вверх, сжатые волокна внизу, растянутые - вверху) изгибающий момент считается отрицательным. Здесь: ось X перпендикулярна плоскости рисунка 4.4 и проходит через точку С - центр тяжести (площади) поперечного сечения. При расчете балок и плоских рам M_X обычно обозначается просто M.

• Все ВСФ, показанные на рис. 4.4 ПОЛОЖИТЕЛЬНЫ. И в дальнейшем - неизвестные ВСФ будем предполагать ПОЛОЖИТЕЛЬНЫМИ. Тогда полученные в результате решения значения (включая знак) легко понять.

Эпюры ВСФ

График зависимости величины какого-либо ВСФ от координаты z поперечного сечения, в котором действует этот ВСФ называется ЭПЮРОЙ. Эпюры имеют большое значение в расчетах на прочность, так как позволяют легко определить сечение, в котором брус максимально нагружен (если поперечное сечение одинаково по всей длине бруса). Такое сечение называется ОПАСНЫМ сечением.

ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ

Задача определения наибольших напряжений начинается с поиска сечения, в котором действуют наибольшие внутренние усилия.

Наибольший изгибающий момент в случае прямого поперечного изгиба консольной балки, нагруженной сосредоточенной силой Р (рис. 1.9) будет в сечении А у заделки, так как здесь действует максимальный изгибающий момент, равный МA = Р*а.

Рис. 1.9

Опасное сечение - это поперечное сечение, в котором действуют наибольшие внутренние усилия.

Где будет располагаться опасное сечение в более сложном случае загружения (рис. 1.10) сразу ответить достаточно трудно, так как сосредоточенный изгибающий момент М и распределенная нагрузка q изгибают балку вниз, а сосредоточенная сила Р - вверх, при этом величины моментов от каждого вида нагрузки различны.

Рис. 1.10

Поэтому для сложных случаев загружения необходимо знать закон изменения по длине балки изгибающего момента или другого внутреннего усилия (например, продольной силы N, поперечной силы Q или крутящего момента Мкр).

Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.

Эпюра - это график, изображающий закон изменения внутреннего усилия по длине стержня. Каждая ордината эпюры представляет собой величину усилия в соответствующем поперечном сечении стержня.

Построение эпюр по методу сечений выполняется в четыре этапа.

Из составленных на 4-ом этапе метода сечений уравнений выражаем искомые внутренние силовые факторы: N, Qx, Qy, Мx, Мy и Мz (Мкр).

С использованием полученных выражений строим графики изменения ВСФ - Л/, Мх и т.д. по длине стержня - эпюры.

2.Перемещения и деформации. Линейные и угловые деформации. Полное напряжение. Нормальные и касательные напряжения. Закон Гука при осевом растяжении-сжатии. Коэффициент Пуассона. Силовая и температурная деформации.

Под действием внешних сил твердые тела изменяют свою геометрическую форму, а точки тела неодинаково перемещаются в пространстве. Вектор  , имеющий свое начало в точке А недефор­мированного состояния, а конец в т.   деформированного состояния, называется вектором полного перемещения т. А(рис. 1.5, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

        Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформированного состояния, расположенные на расстоянии S друг от друга (рис. 1.5, б).           

Рис. 1.5

        Пусть в результате изменения формы тела эти точки переместились в положение А и В, соответственно, а расстояние между ними увеличилось на величину S и составило S + S. Величина

                                                                                              (1.6)

называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы _x , _y , _z .

        Линейные деформации _x , _y , _z характеризуют изменения объема тела в процессе деформирования, а формоизменения тела  угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрезками ОD и ОС (рис. 1.5, б). При действии внешних сил указанный угол DOC изменится и примет новое значение DOC. Величина

                            ( DOC   DOC) =                        (1.7)

называется угловой деформацией, или сдвигом в точке О в плоскости СОD. Относительно координатных осей деформации сдвига обозначаются _xy , _xz , _yz .

        Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформированное состояние в точке.

Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м² (МПа = 10⁶ Н/м², кгс/см²=98 066 Па ≈ 10⁵Па, тс/м² и т. д.).

Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим∆R . Полное среднее напряжение на этой площадке р =∆R ∆A . Найдем предел этого отношения при ∆A 0 . Это и будет полным напряжение на данной площадке (точке) тела. 

p =lim A 0 A R

Полное напряжение p , как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σ_n и касательное к площадке – касательное напряжение  n. Здесь n – нормаль к выделенной площадке1.

Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением –  nx ny. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

p =      n  nx  nx       

Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением p , а с его составляющими σx xy xz . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.