Метод Лагранжа и метод Гаусса

§

В этом и последующих пунктах существенно потребуется знание МЕТОДА ГАУССА преобразования систем линейных уравнений.

П

Пример. Рассмотрим матрицу квадратичной формы

из предыдущих пунктов, и, временно выходя из круга поставленных в настоящем разделе задач, побробуем применить к ней метод Гаусса приведения к треугольному виду:

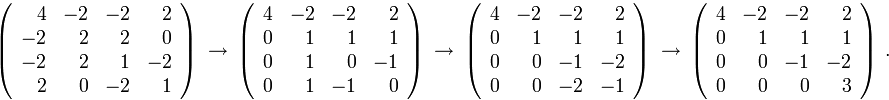
Обратим внимание на два обстоятельства: диагональные элементы последней матрицы совпадают с коэффициентами канонического вида квадратичной формы, а коэффициенты замены переменных, приводящей к этому каноническому виду, совпадают с элементами строк этой матрицы, если их разделить на соответствующие диагональные элементы. Возникает подозрение , что метод Лагранжа является «замаскированной» версией метода Гаусса. ♦

Для того, чтобы выяснить аналитический смысл преобразований по методу Лагранжа найдем правило формирования коэффициентов в первом шаге приведения квадратичной формы к каноническому виду. Пусть исходная квадратичная форма записана в виде

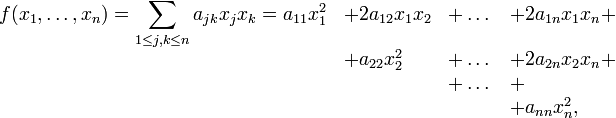
т.е. коэффициенты при смешанных произведениях переменных записаны с выделением множителя . После выделения полного квадрата, содержащего переменные :

в правой части тождества образовалась квадратичная форма , не содержащая . Она равна

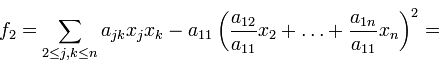
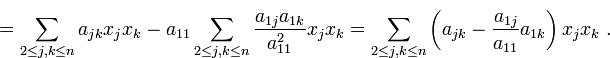
Если теперь выписать матрицу этой квадратичной формы (она имеет порядок ), то ее элементы образуются по точно такому же правилу, как и коэффициенты матрицы, получающейся из матрицы в результате первого шага метода Гаусса.

Т

Теорема. Метод Лагранжа приведения квадратичной формы к каноническому виду эквивалентен методу Гаусса приведения матрицы к треугольному виду.

Доказательство. Действительно, первый шаг прямого хода метода исключения переменных Гаусса преобразует матрицу следующим образом:

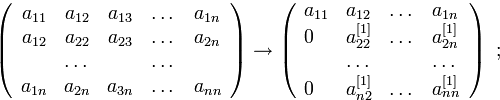
здесь

и предполагается, что . Видим, что формула формирования элементов матрицы

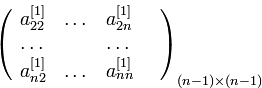
точно такая же, как и матрицы квадратичной формы . Более того, поскольку матрица симметрична ( ), то и только что полученная матрица оказывается симметричной. Если , то к этой новой матрице можно снова применить ту же процедуру, и т.д., и в конце концов придем к матрице первого порядка. Собирая все промежуточные результаты в одну матрицу, получим ее в треугольном виде

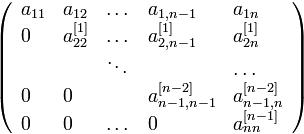
при условии, что ни одно из чисел на диагонали не обратилось в нуль:

Если теперь обратиться к методу Лагранжа, то увидим, что полученная матрица как раз и определяет замену переменных

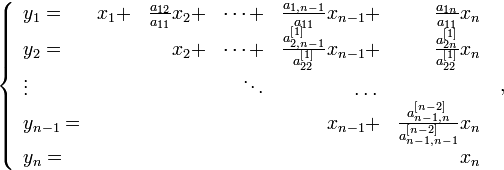
приводящую квадратичную форму к каноническому виду:

Приведение квадратичных форм к каноническому виду

            Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂

y₂ = a₁₂x₁ + a₂₂x₂

где у₁ и у₂ – координаты вектора  в базисе .

            Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁ + х₂у₂.

 

            Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁ и х₂ – скалярное произведение .

            Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

            Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

            При переходе к новому базису от переменных х₁ и х₂ мы переходим к переменным  и . Тогда:

 

            Тогда .

Выражение  называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

 

Пример. Привести к каноническому виду квадратичную форму

Ф(х₁, х₂) = 27.

 

Коэффициенты: а₁₁ = 27,   а₁₂ = 5,   а₂₂ = 3.

Составим характеристическое уравнение: ;

(27 - )(3 - ) – 25 = 0

² - 30 + 56 = 0

₁ = 2;   ₂ = 28;

 

 

Пример. Привести к каноническому виду уравнение второго порядка:

17x² + 12xy + 8y² – 20 = 0.

 

Коэффициенты а₁₁ = 17,   а₁₂ = 6,   а₂₂ = 8.      А =

Составим характеристическое уравнение:

(17 - )(8 - ) - 36 = 0

136 - 8 - 17 + ² – 36 = 0

² - 25 + 100 = 0

₁ = 5,     ₂ = 20.

Итого:  - каноническое уравнение эллипса.

 

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

            Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим ₁ = 2, ₂ = 6.

Найдем координаты собственных векторов:

полагая m₁ = 1, получим  n₁ =

полагая m₂ = 1, получим  n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

 

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

            Решение: Составим характеристическое уравнение квадратичной формы : при

Решив это уравнение, получим ₁ = 1, ₂ = 11.

Найдем координаты собственных векторов:

полагая m₁ = 1, получим  n₁ =

полагая m₂ = 1, получим  n₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

 

            Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

4ху + 3у² + 16 = 0

 

Коэффициенты: a₁₁ = 0;    a₁₂ = 2;    a₂₂ = 3.

Характеристическое уравнение:

Корни: ₁ = -1,   ₂ = 4.

Для ₁ = -1                                          Для ₂ = 4

                                  

 

m₁ = 1;     n₁ = -0,5;                                 m₂ = 1;    n₂ = 2;

 

= (1; -0,5)                                            = (1; 2)

                                                

                             

Получаем:   -каноническое уравнение гиперболы.

Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.

Пусть квадратичная форма имеет в каком-то базисе матрицу

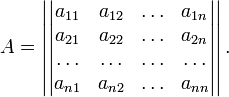
Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры Δ_i положительны. Форма отрицательно определена, если и только если знаки Δ_i чередуются, причём Δ₁ < 0. Здесь главными минорами матрицы A называются определители вида

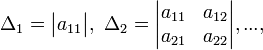
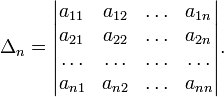
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица

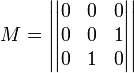
не является неотрицательно определённой — так как, например, (Mv,v) = − 2 для v = (0,1, − 1). В то же время все её главные миноры равны 0, то есть неотрицательны.

Содержание  [убрать]  1 Доказательство 1.1 Критерий положительной определённости квадратичной формы 1.2 Критерий отрицательной определённости квадратичной формы 2 См. также 3 Источники