Квадратичная форма

означает одно из множеств: рациональных, или вещественных, или комплексных чисел.

Определение

Квадратичной формой над множеством называют однородный полином второй степени с коэффициентами из ; если переменные обозначить , то общий вид квадратичной формы от этих переменных:

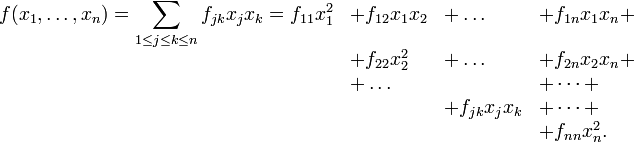
П

Функции

являются квадратичными формами. Функции

не являются квадратичными формами.

Заметим, что в выражении для квадратичной формы присутствуют как квадраты переменных так и их смешанные произведения . Говорят, что квадратичная форма имеет канонический вид если в ее представлении все коэффициенты при смешанных произведениях переменных равны нулю, т.е. она имеет вид

говорят также, что форма является «суммой квадратов»1).

Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.

П

Пример.

А в общем случае:

при — константах. Такое представление оказывается достаточно удобным для анализа квадратичной формы — например, в случае вещественных форм, при проверке выполнимости неравенства вида . Приведенные выше примеры показывают неоднозначность представления в виде суммы квадратов: вид квадратов и даже их количество для одной и той же формы могут быть различными. С целью обеспечения некоторой унификации установим некоторое дополнительное ограничение — потребуем, чтобы линейные однородные формы

были линейно независимыми. При таком ограничении любое представление квадратичной формы в виде суммы квадратов называется каноническим видом квадратичной формы.

Задача. Для произвольной квадратичной формы построить (хотя бы один) ее канонический вид.

!

Поставленная задача имеет существенное значение для анализа

• произвольного полинома 2) нескольких переменных на максимумы и минимумы;

• геометрии линий второго порядка на плоскости и поверхностей второго порядка в пространстве; например, по набору коэффициентов уравнения, задающего кривую

определить к какому типу (эллипс, гипербола, парабола,…) она относится.

Метод Лагранжа приведения квадратичной формы к каноническому виду

Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.

Метод Лагранжа

1. Пусть . Выделим в все слагаемые, содержащие :

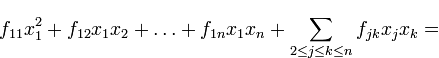
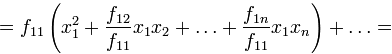
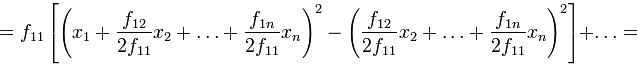
В последнем представлении первое слагаемое представляет собой квадрат линейной формы по переменным ; все оставшиеся слагаемые не зависят от , т.е. составляют квадратичную форму от переменных . Таким образом, исходная задача для формы переменных оказывается сведенной к случаю формы -й переменной; последняя преобразуется по аналогичному принципу.

2. Если , но , т.е. при хотя бы одном квадрате переменной коэффициент отличен от нуля. Алгоритм модифицируется таким образом, что выделение полного квадрата начинается с переменной вместо — первая ничем не лучше (и не хуже) -й!

3. Совсем исключительный случай: квадраты переменных вообще отсутствуют, т.е. . Выбираем один из ненулевых коэффициентов при смешанных произведениях переменных: пусть . Представляем и заменяем все вхождения переменной на при вспомогательной переменной . В новой квадратичной форме уже присутствует квадрат переменной с ненулевым коэффициентом. Тем самым этот случай сводится к предыдущему. После приведения новой формы к сумме квадратов возвращаемся к «старой» переменной .

П

Пример. Привести форму

к каноническому виду.

Решение.

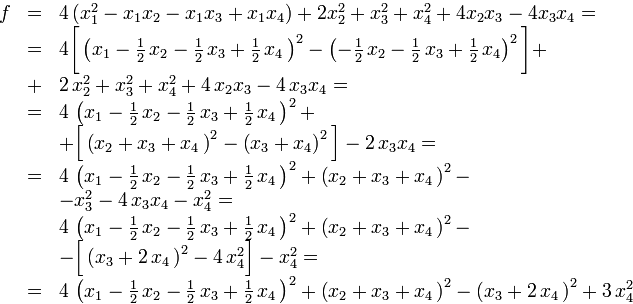
Ответ. .

П

Пример. Привести форму

к каноническому виду.

Решение.

В соответствии с алгоритмом, на следующем шаге нужно выделять слагаемые, содержащие переменную , но коэффициент при в правой части формулы обратился в нуль. Поэтому — в соответствии с пунктом 2 метода — приходится выделять квадрат на основе переменной :

Ответ. .

П

Пример. Привести форму

к каноническому виду.

Решение. Коэффициенты при квадратах переменных все равны нулю. Действуем в соответствии с пунктом 3 метода Лагранжа. Поскольку коэффициент при отличен от нуля, делаем замену переменной при :

Дальнейший ход решения — в соответствии с пунктом 1 метода Лагранжа:

Получили сумму квадратов форм от переменных . Возвращаемся к переменной :

Ответ. .

§

Метод Лагранжа позволяет получить канонический вид квадратичной формы над тем же множеством , над которым рассматривается исходная форма — например, если коэффициенты формы являются рациональными, то и коэффициенты ее канонического вида (т.е. числа ) будут также рациональными.