2.3 Разработка алгоритма

Из предыдущего раздела можно выделить следующие этапы, которые должна выполнять программа:

1. Определить функцию;

2. Ввести приближение и точность;

3. Найти градиент;

4. Найти на направлении против градиента точку, соответствующую минимуму функции и лежащую на градиенте;

5. Сравнить эту точку с предыдущей. Если разница между текущей и предыдущей точкой меньше точности, то последний результат и есть минимум функции, в противном случае вернуться к шагу 3, взяв за новое приближение последний результат.

Чтобы программа была, как можно больше унифицирована, она не должна зависеть ни от вида функции, ни от её производных. Так как вычислять производную символьно – это трудоёмкий процесс, проще вычислять её численно.

Градиент – это производная скалярной функции, определенной на векторном пространстве. Для численного вычисления градиента будем пользоваться следующей формулой [1, стр.72]

, (2.5)

где h – некоторое положительное число.

Следует подходить ответственно к выбору числа h, так как слишком большие и слишком маленькие его значения сильно искажают результат. Для функции (2.1) можно брать шаг 0,9 или 1. Данные результаты получены опытным путём.

Формула (2.4) очень сложна, поэтому поиск минимума на направлении антиградиента лучше всего проводить численно. В данной реализации осуществлять это будем по следующему алгоритму:

1. Задаем начальную опорную точку;

2. Делаем какой-то шаг относительно опорной точки в сторону антиградиента;

3. Решаем задачу одномерной оптимизации (поиск минимума) в промежутке от опорной точки, до точки, в которую мы попали после отступа.

4. Если в результате оптимизации минимумом оказалась граница данного промежутка, то делаем опорной точкой эту границу и возвращаемся в пункт 2, в противном случае результат – это и есть минимум.

Одним из простых алгоритмов одномерной оптимизации является троичный поиск [5]. При троичном поиске некоторый отрезок делится на три равные части, при этом определены четыре точки: исходные границы (внешние точки) и две точки внутри границ. Затем вычисляется значение функции во внутренних точках. В зависимости от результата устанавливается новый промежуток, одной границей которого будет внешняя точка, а другой какая-то внутренняя точка. Затем все действия повторяются с новыми границами. Общий принцип троичного поиска показан на рисунке 2.2. Например, новый интервал на рисунке 2.2 будет образован из точки a₀ и x₂, так как минимум лежит между этими точками. Процесс повторяется, пока интервал не станет требуемой длины, задаваемой точностью.

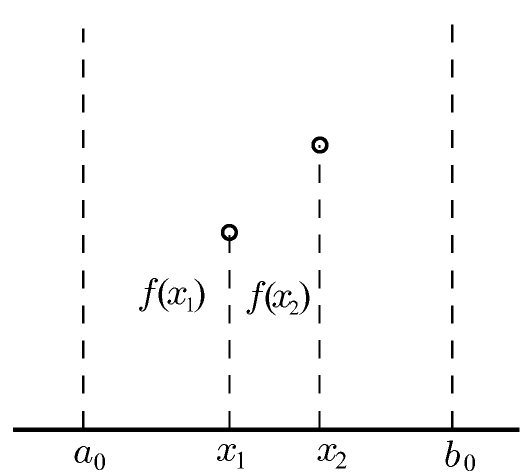
Рисунок 2.2 Метод троичного поиска

Из всего выше изложенного можно представить алгоритм графически (рисунок 2.3).

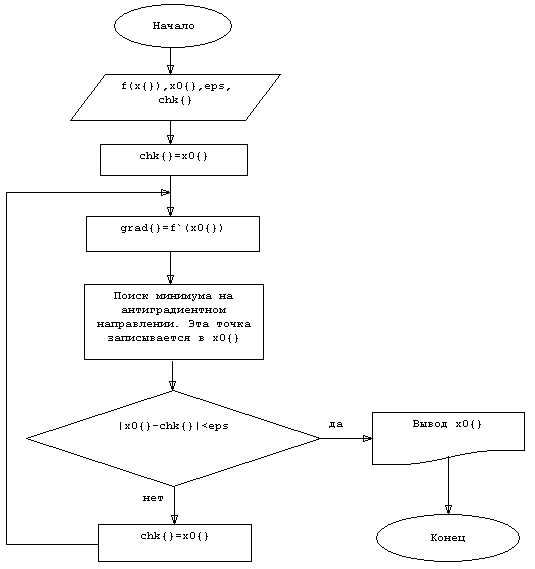
Рисунок 2.3 Метод наискорейшего спуска

Алгоритм троичного поиска представим в виде структурограммы (рисунок 2.4).

Ввод X1{x1i}0…n, X2{x2i}0…n, eps
	leftTh{ai}0…n=(X12+X2)/3
	rightTh{bi}0…n=(X1+2X2)/3
	f(leftTh)<f(righTh) да		нет
	X2=rightTh		X1=leftTh
	length=0
	для i от 0
		length=length+(x2i-x1i)2
	до n
	length=
пока length>eps
Вывод (X1+X2)/2

Рисунок 2.4 Метод троичного поиска