1.2 Формализация задачи

Так как запись значений функции в файл – тривиальная задача, перейдем к описанию метода МНК.

МНК ищет параметры эмпирической формулы вида

.

Поиск параметров осуществляется из условия минимума функции S

, (1.2)

которая является ничем иным, как суммой квадратов остатков регрессии [1, стр. 66].

На практике наиболее часто используется случай, когда эмпирическая формула является линейной по неизвестным параметрам а₀, a₁, …, a_m, т.е. её можно представить в виде

. (1.3)

В частности функция (1.1) такой и является. Если (1.3) подставить в (1.2) и приравнять к нулю все частные производные по неизвестным параметрам, то можно прийти к следующей системе алгебраических линейных уравнений [1, стр. 67]

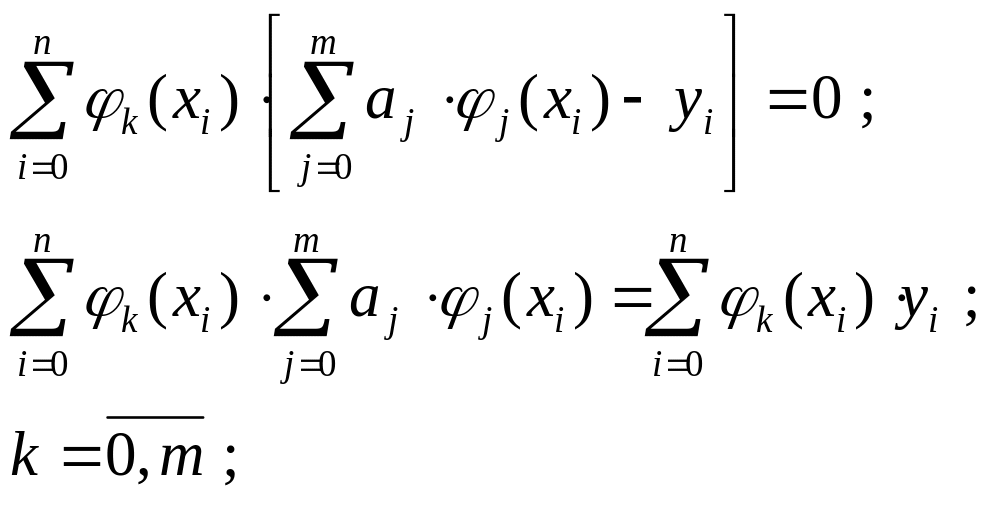(1.4)

где (x) – эмпирическая формула;

a_j – неизвестные параметры эмпирической формулы;

y_i – опытное значение.

Систему (1.4) можно представить в более наглядной матрично-векторной форме

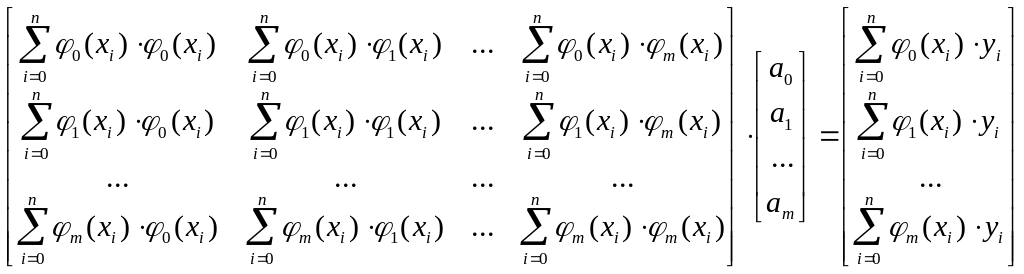. (1.5)

Параметры эмпирической формулы находятся решением системы (1.5). Так как матрица в (1.5) всегда квадратная размером m x m, то ее можно решить прямым методом, например методом Гаусса.

Метод Гаусса состоит из двух этапов:

• Прямой ход (матрица, составленная из коэффициентов системы линейных уравнений, приводится к треугольному виду);

• Обратный ход (получение корней системы).

Метод Гаусса применим, если ранг исходной матрицы равен рангу матрицы расширенной. Можно не вычислять ранг отдельно, так как несовместность устанавливается после приведения матрицы к треугольному виду, появлением хотя бы одного нуля на главной диагонали.

1.3 Разработка алгоритма

Первая программа является наиболее простой, поэтому начнем с неё. Совершенно очевидно, что первая программа должна работать по алгоритму, показанному на рисунке 1.1.

В данной блок-схеме под f(x) понимается функция (1.1), под g(sgm) понимается некоторая функция, которая возвращает случайное число, подчиняющееся нормальному распределению, с заданной дисперсией sgm.

Генерация случайного значения в данной задаче (как будет показано в следующем разделе) основана на центральной предельной теореме, т.е. случайное число получается суммой большого числа случайных чисел с равномерным распределением.

Общий алгоритм работы второй программы показан на рисунке 1.2. Блоки прямого хода, обратного хода и заполнение исходной матрицы со свободным вектором, для экономии места, представим в нотации Найси-Шнайдермана (так называемые структурограммы [1, стр.286]). На рисунке 1.3 показана струкутрограмма алгоритма заполнения исходной матрицы и свободного вектора, а на рисунке 1.4 показана структурограмма метода Гаусса. В структорограмме рисунка 1.3 под массивом Y{} понимается файл с точками. Так же следует обратить внимание на то, что, хотя нумерация элементов массивов и идет с нуля, следует передавать размер массива натуральным числом. Запись вида A{a_i,j=0}_{m x m} подразумевает двумерный массив размером m x m, заполненный при передаче нулевыми элементами. Индексация элементов в массивах при такой записи всегда от 0 и до m-1.

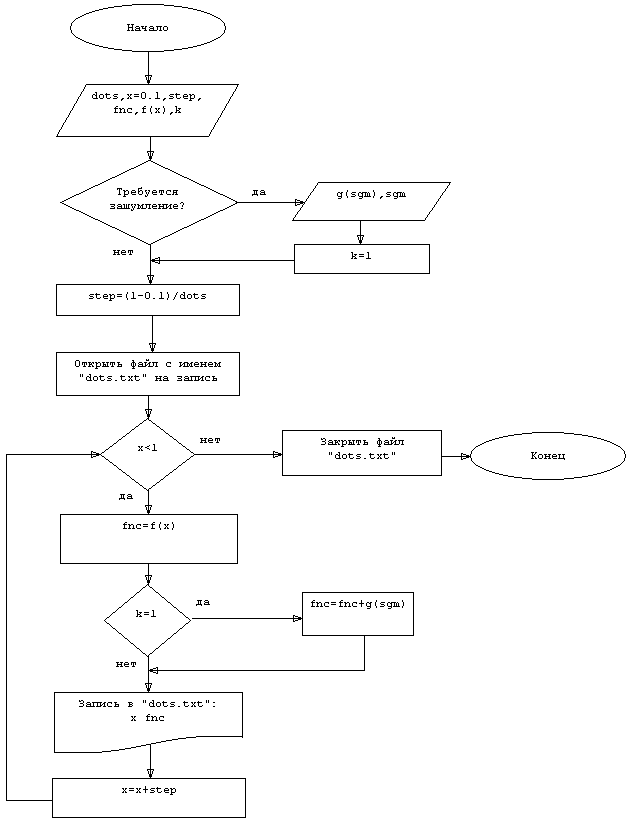
Рисунок 1.1 Алгоритм работы программы создания точек

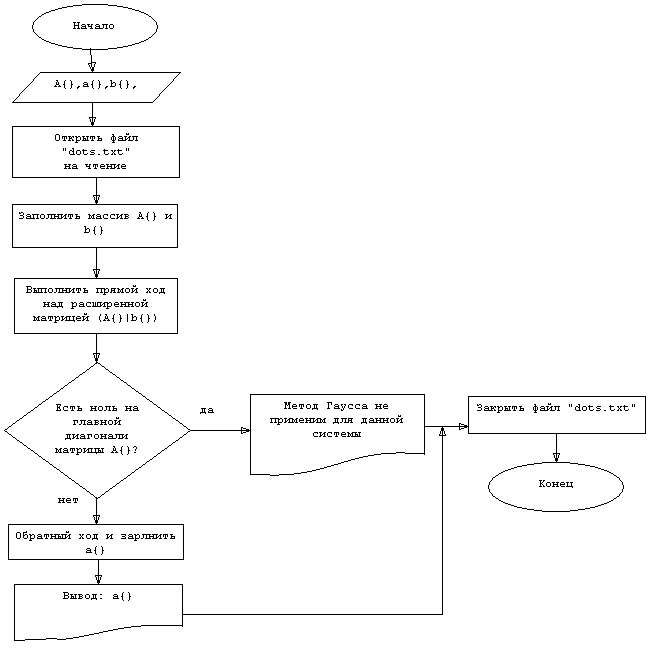
Рисунок 1.2 Алгоритм работы программы аппроксимации

# Под m здесь понимается реальный размер, как это принято в математике. Индексация многомерных массивов начинается с нуля и заканчивается m-1.
Ввод A{ai,j=0}m x m, b{bi = 0}0…m-1, Y{xi, yi}0…n
для i от 0
	для k от 0
		для j от k
			ak, j = ak, j + k(xi)  j(xi)
			kj да	нет
			aj, k =ak, j
		до m-1
		bk = bk + k(xi)  yi
	до m-1
до n
Вывод A{ai,j}m x m, b{bi }0…m-1

Рисунок 1.3 Подготовка массивов для обработки

# Под m здесь понимается реальный размер, как это принято в математике. Индексация многомерных массивов начинается с нуля и заканчивается m-1.
Ввод A{ai,j}m x m, a{ai}0…m-1, b{bi = 0}0…m-1
для k от 0
	для i от k+1
		W = ai, k / ak, k
		для j от k
				ai, j = ai, j – W ak, j
		до m-1
		bi = bi – W bk
	до m-1
до m-2
W=1
для i от 0
	W = W ai, i
до m-1
W=0 да		нет
		для i от m-1
			s=0
			для j от i
					s=s+ai, jaj
			до m-1
			ai = (bi – s) / ai, i
		до 0
		Вывод a{ai}0…m-1

Рисунок 1.4 Структурограмма метода Гаусса

Запись вида b{b_i = 0}_0…m-1 подразумевает вектор (или одномерный массив), заполненный при передаче нулевыми значениями. Снизу справа определяется индексация элементов в массиве.

Структурограммы легко переводятся на процедурные языки программирования и также легко читаются.