1.5 Анализ результатов

Для начала создадим файл с пятьюдесятью точками без зашумления. На рисунке 1.5 показана работа программы.

Рисунок 1.5 Создаём 50 точек без шума

Файл с точками будет иметь вид, показанный на рисунке 1.6.

Рисунок 1.6 Файл с точками

Теперь запускаем вторую программу. Так как выборка незашумленная, а эмпирическая формула совпадает с законом, по которому эта выборка получена, то параметры эмпирической формулы должны быть равны 1. На рисунке 1.7 видно, что это с достаточной точностью так.

Рисунок 1.7 Результат работы второй программы

Теперь будем зашумлять результат. В таблице 1 приведены результаты работы второй программы при различных дисперсиях шума. На рисунках 1.9, 1.10 и 1.11 показаны формы эмпирических формул. Для наглядности они показаны вместе с графиком функции (1.1). Так как выборка случайна, то параметры будут меняться от запуска к запуску.

Таблица 1

Значение дисперсии	Объем выборки	Значения параметров эмпирической формулы
0,05	50	0,9522
		0,6394
		0,6479
		1,4488
0,1	50	1,1237
		1,8473
		1,1806
		0,6560
0,5	50	1,3681
		4,5206
		5,6668
		-4,9306

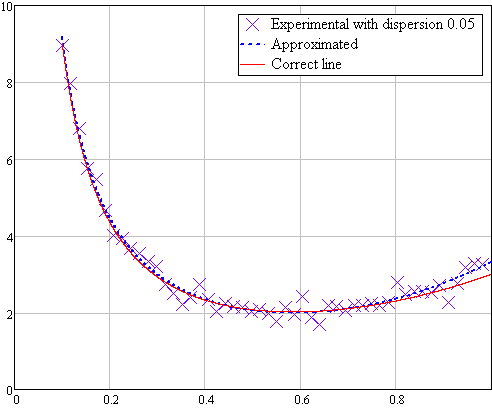
Рисунок 1.9 Аппроксимация случайной выборки с дисперсией 0,05

На графиках хорошо видно, что наиболее удачно аппроксимация прошла при дисперсии 0,1. В других случаях большое отклонение объясняется малым объемом выборки.

Продемонстрируем случай, когда аппроксимация не произойдет. Для этого попробуем обработать выборку из шести точек. Результат работы второй программы показан на рисунке 1.12.

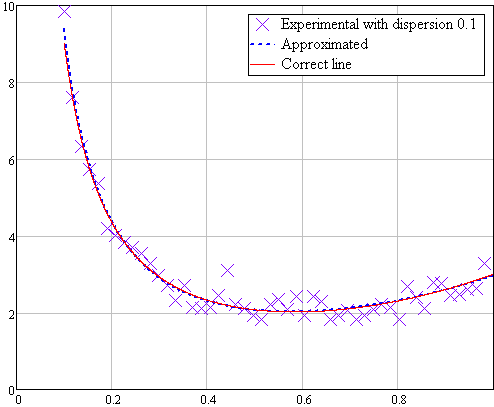
Рисунок 1.10 Аппроксимация случайной выборки с дисперсией 0,1

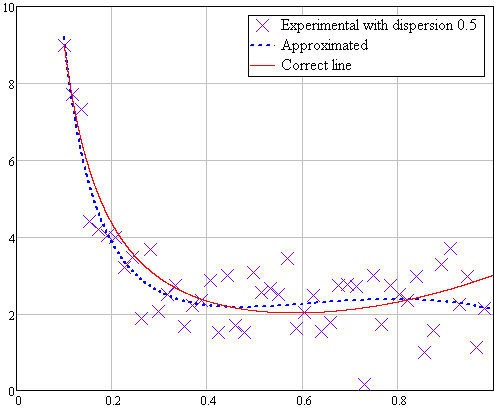
Рисунок 1.11 Аппроксимация случайной выборки с дисперсией 0,5

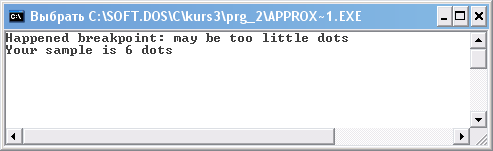
Рисунок 1.12 Аварийный останов при выполнении прямого хода

2Многомерная оптимизация

2.1 Постановка задачи

Дана функция многих переменных

. (2.1)

Методом наискорейшего спуска найти минимум функции (2.1). Пользователь должен вводить начальное приближение и точность. Критерием остановки считать

. (2.2)

2.2 Формализация задачи

Метод наискорейшего спуска является вариантом градиентного спуска [4]. Основной идеей метода градиентного спуска заключается в том, чтобы осуществлять оптимизацию в направлении антиградиента -f, определяющего направление наискорейшего спуска.

Словами алгоритм можно описать так: повторять операцию

, (2.3)

где x^[k] – вектор аргументов функции многих переменных текущей итерации;

-f(x^[k]) – антиградиент функции f, от аргументов текущей итерации;

^[k] – шаговый вектор, определяющий скорость движения в сторону антиградиента;

до тех пор, пока не выполниться условие (2.2).

Метод наискорейшего спуска, как варианта градиентного спуска, основывается на выборе шага из следующего соображения

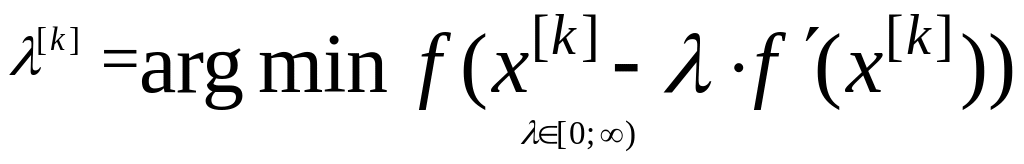. (2.4)

Чтобы понять запись (2.4), приведем геометрическую интерпретацию метода, показанную на рисунке 2.1. На рисунке начальное приближение это точка x⁰.

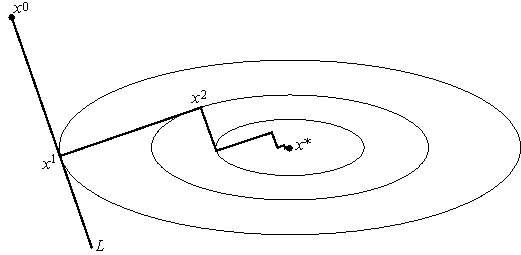
Рисунок 2.1 Геометрическая интерпретация наискорейшего спуска

Из этой точки мы движемся в сторону антиградиента, соответствующего лучу L. На следующем этапе мы попадаем в новую точку x¹ через шаговый вектор, который в данном случае определяет такое расстояние от предыдущей точки, которое нужно пройти, чтобы оказаться в минимуме функции f на направлении L. Именно об этом и говорит запись (2.4). Затем мы повторяем вышеизложенное уже относительно x¹ и так далее, пока не выполнится условие (2.2).