
1.Билет
Изоморфизм конечномерных линейных пространств
Определение. Линейные
пространства ![]() и
и ![]() называются
изоморфными, если между их элементами
можно установить такое взаимно однозначное
соответствие, что если
векторам
называются
изоморфными, если между их элементами
можно установить такое взаимно однозначное
соответствие, что если
векторам ![]() и
и ![]() из
соответствуют
векторы
из
соответствуют
векторы ![]() и
и ![]() из
,
то вектору
из
,
то вектору ![]() соответствует
вектор
соответствует
вектор ![]() и
при любом
и
при любом ![]() вектору
вектору ![]() соответствует
вектор
соответствует
вектор ![]() .
.
Теорема. Любые два n-мерных линейных пространства изоморфны.
Теорема на лекции доказана.
Это
означает, что все ![]() -мерные
линейные пространства “устроены”
одинаково — как пространство
-мерные
линейные пространства “устроены”
одинаково — как пространство ![]() векторов-столбцов
из
действительных
чисел, т.е. что все они изоморфны пространству
.
векторов-столбцов
из
действительных
чисел, т.е. что все они изоморфны пространству
.
Изоморфизм -мерных линейных пространств пространству означает, что соотношения между элементами -мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из и операции с ними и что всякое утверждение относительно векторов из справедливо для соответствующих элементов любого -мерного линейного пространства.
2.Билет
Ма́трицей
перехо́да от базиса ![]() к базису
к базису ![]() является матрица,
столбцы которой — координаты
разложения векторов
в базисе
.
является матрица,
столбцы которой — координаты
разложения векторов
в базисе
.
Обозначается ![]()
Так как
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Матрица перехода это

При
умножении столбца, составленного из
коэффициентов разложения вектора
по базису ![]() ,
на матрицу, обратную к матрице перехода,
мы получаем тот же вектор, выраженный
через базис
,
на матрицу, обратную к матрице перехода,
мы получаем тот же вектор, выраженный
через базис ![]() .
.
Из-за
того, что уменьшает объём работы при
переводе векторов аффинных
пространств и
в пространстве столбцов ![]() в
другие базисы, используется в трёхмерном
моделировании.
в
другие базисы, используется в трёхмерном
моделировании.
[править]Пример
Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:
![]()
Свойства
Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.

3.Билет
Линейное,
или векторное
пространство ![]() над полем
над полем ![]() —
это непустое
множество
—
это непустое
множество ![]() ,
на котором введены операции
,
на котором введены операции
сложения, то есть каждой паре элементов множества
 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый  и
иумножения на скаляр (то есть элемент поля ), то есть любому элементу
 и
любому элементу
и
любому элементу  ставится
в соответствие единственный элемент
из
,
обозначаемый
ставится
в соответствие единственный элемент
из
,
обозначаемый  .
.
При этом на операции накладываются следующие условия:
 ,
для любых
(коммутативность
сложения);
,
для любых
(коммутативность
сложения); ,
для любых
,
для любых  (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
 ,
что
,
что  для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;
для
любого
(существование
нейтрального элемента относительно
сложения),
в частности
не
пусто;для любого существует такой элемент
 ,
что
,
что  (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).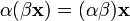 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр); (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор). (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров); (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества называют векторами, а элементы поля — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
Простейшие свойства
Векторное пространство является абелевой группой по сложению.
Нейтральный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
.Для любого противоположный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
. для
любых
для
любых  и
.
и
. для
любого
.
для
любого
.
Подпространство
Алгебраическое
определение: Линейное
подпространство или векторное
подпространство ―
непустое подмножество ![]() линейного
пространства
такое,
что
само
является линейным пространством по
отношению к определенным в
действиям
сложения и умножения на скаляр. Множество
всех подпространств обычно обозначают
как
линейного
пространства
такое,
что
само
является линейным пространством по
отношению к определенным в
действиям
сложения и умножения на скаляр. Множество
всех подпространств обычно обозначают
как ![]() .
Чтобы подмножество было подпространством,
необходимо и достаточно, чтобы
.
Чтобы подмножество было подпространством,
необходимо и достаточно, чтобы
 ;
;для всякого вектора
 ,
вектор
,
вектор  также
принадлежал
,
при любом
;
также
принадлежал
,
при любом
;для всяких векторов
 ,
вектор
,
вектор  также
принадлежал
.
также
принадлежал
.
Последние два утверждения эквивалентны следующему:
для
всяких векторов
,
вектор ![]() также
принадлежал
для
любых
также
принадлежал
для
любых ![]() .
.
В
частности, пространство, состоящее из
одного элемента ![]() ,
является подпространством любого
пространства; любое пространство
является само себе подпространством.
Подпространства, не совпадающие с этими
двумя, называют собственными илинетривиальными.
,
является подпространством любого
пространства; любое пространство
является само себе подпространством.
Подпространства, не совпадающие с этими
двумя, называют собственными илинетривиальными.
