
- •1. Основные понятия
- •2. Динамическое представление сигналов
- •5. Ряды Фурье периодических сигналов
- •7. Спектральное представление одиночных сигналов. Интеграл Фурье. Спектры гауссовского сигнала, ф-ции Дирака, Хевисайда
- •12. Свойства автокорреляционной функции.
- •1 3. Функция автокорреляции дискретных сигналов
- •6. Спектральное представление одиночных сигналов. Интеграл Фурье. Спектры постоянного напряжения, гармонического сигнала, прямоугольного и ам импульса.
- •15. Амплитудно-модулированный радиосигнал
- •16. Дискретизация узкополосных сигналов
- •17. Сигналы с угловой модуляцией. Чм и фм.
- •18. Сигналы с угловой модуляцией. Чм и фм.
- •19. Принципы построения вч модуляторов
- •14. Виды модуляции. Условие узкополосности
5. Ряды Фурье периодических сигналов
периодический сигнал - для которого справедливо выр-е: x(t)≡x(t-mT) где Т - период
Введём ортонормированный
базис:
![]() ,
где
,
где
![]() .
.
Из формулы
следует:
![]()
это ряд Фурье в комплексной форме.
Воспользовавшись
формулой Эйлера
![]() ,
,
запишем тригонометрическую форму этого ряда:
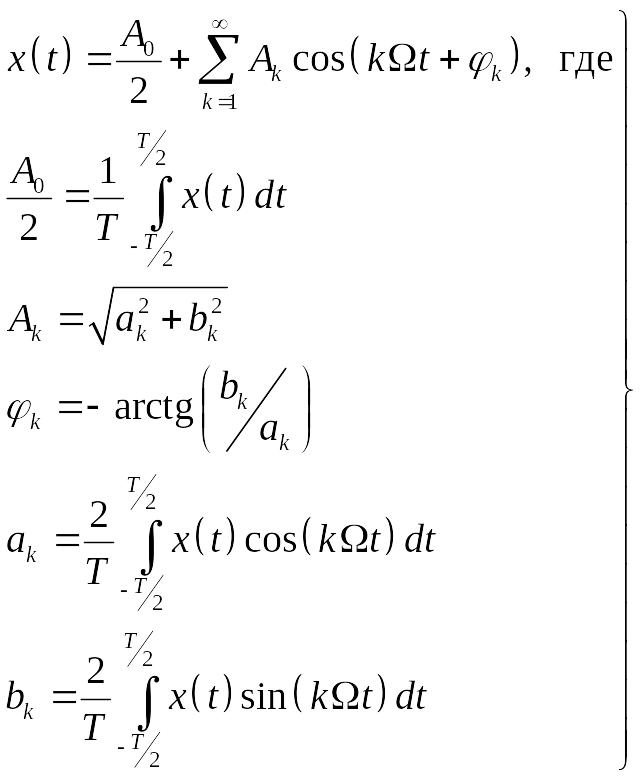
Существует ещё
одна форма ряда: если
![]() ,
,
тогда
![]()
Д ля
анализа спектров используются спектральные
диаграммы, показывающие зависимости
величин Ak
и φk
от номера k
ля
анализа спектров используются спектральные
диаграммы, показывающие зависимости
величин Ak
и φk
от номера k
примеры вычисления спектров:
1)
![]()
график функции rect(t) и график функции x(t):
![]()
![]()
Вычислим коэффициенты разложения Ck:
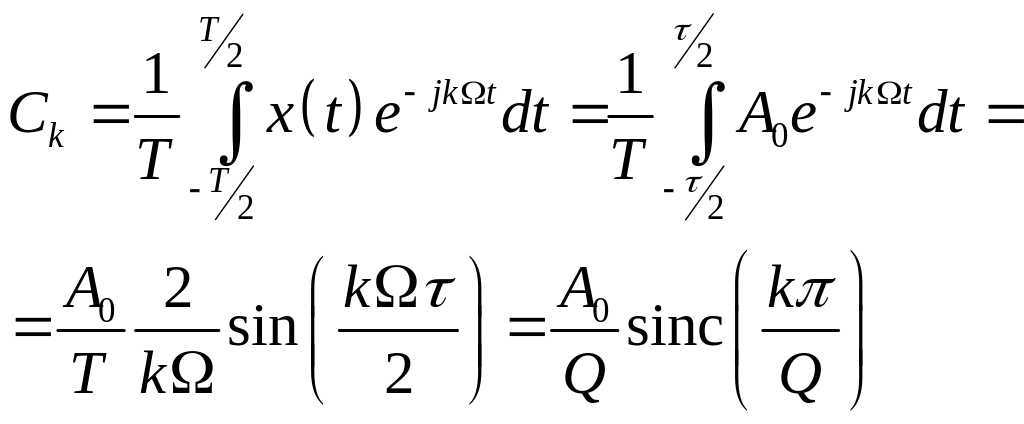
где Q=T/ - скважность сигнала (обратная величина α=/T - коэффициент заполнения).
Скважность - важная характеристика сигнала, сигнал, обладающий большой скважностью имеет богатый спектр.
частный случай при Q=2. получается - меандр:
Для такого сигнала тригонометрический ряд Фурье будет иметь вид:
![]()
Если математически найти сумму этого ряда, то сигнал не будет точно иметь форму меандра, Он обладает отростками, высота которых составляет 18% от амплитуды сигнала. При практических измерениях эти отростки не фиксируются. Потому что при большом значении k ширина этих отростков не обладает никакой энергией, и прибор не фиксирует эти отклонения формы.
![]()
![]()
25.

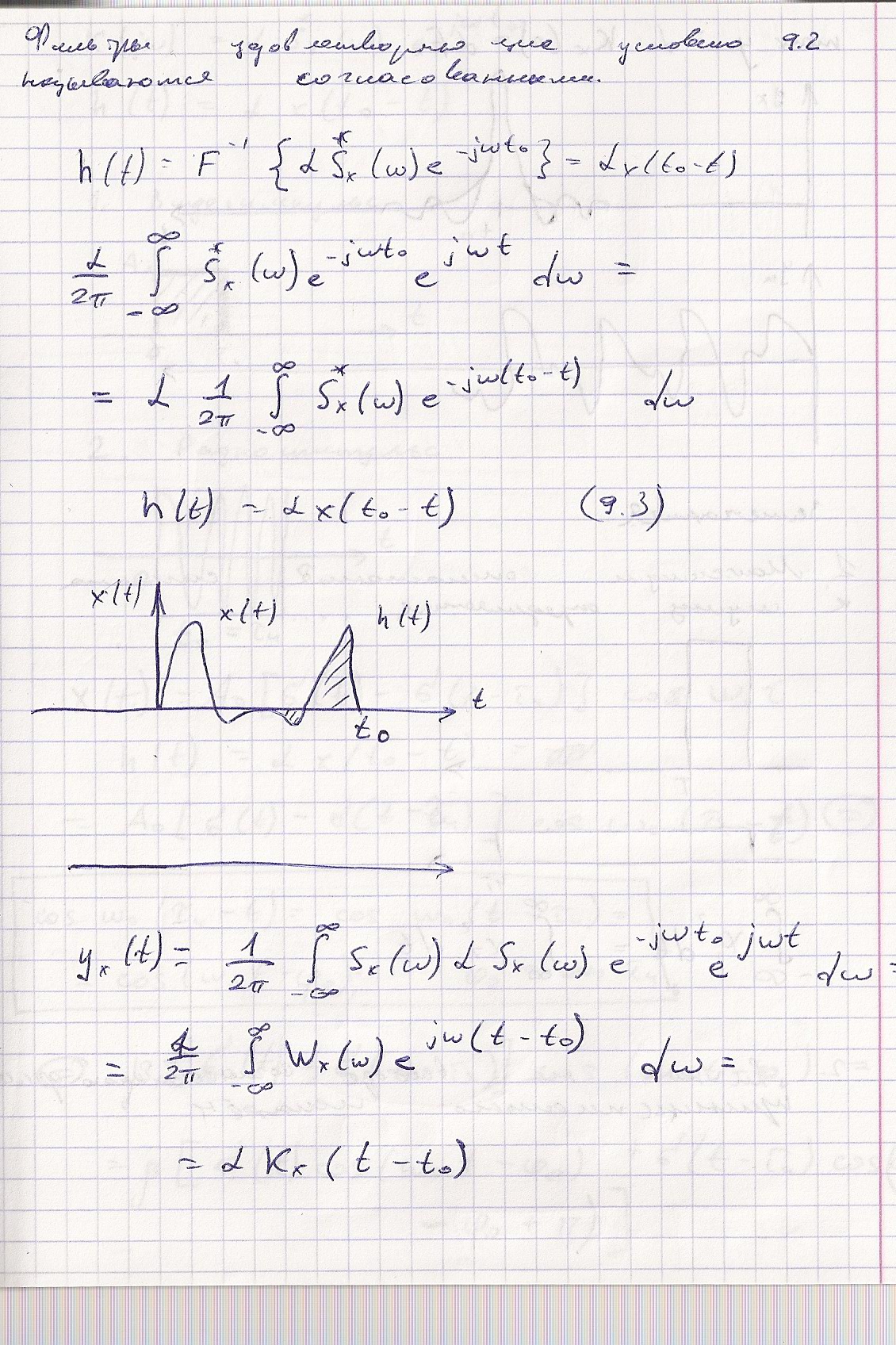
7. Спектральное представление одиночных сигналов. Интеграл Фурье. Спектры гауссовского сигнала, ф-ции Дирака, Хевисайда
Пусть сигнал x(t)
- одиночный импульс конечной длительности.
мысленно представим периодическую
последовательность, которая может быть
представлена в виде ряда Фурье:
![]() ,
где
,
где
![]() .
.
устремим к бесконечности интервал наблюдения T∞. И вернёмся к одиночному импульсу
Р/м базисные функции вида:
![]() ,
где
,
где
![]() .
.
функция (s,t)
описывается выражением
![]() .
Тогда
.
Тогда
![]() ,
,
а сигнал представим
в виде
![]() .
.
Распишем теперь Ck как скалярное произведение:
![]()
Устремим в этом соотношении T∞., тогда d, а дискретная переменная стремится к непрерывной: k. и для x(t) получим:
![]() ,
,![]() (1)
(1)
В формуле (1) внутреннее скалярное произведение - прямое преобразование Фурье,
а внешнее – обратное преобразование Фурье. Запишем их в виде системы:
![]()
![]() - спектральная
плотность сигнала x(t)
или интеграл
Фурье. краткая
форма записи:
- спектральная
плотность сигнала x(t)
или интеграл
Фурье. краткая
форма записи:
![]() ;
;
![]()
или
![]() .
.
такое преобразование
справедливо только для абсолютно
интегрируемых сигналов, т.е. для сигналов,
для которых справедливо выражение:
![]() .
.
Спектральная плотность функции Гаусса.
![]() -
-
это интеграл Пуассона, он справедлив при C<∞.
Рассмотрим такое
выражение:
![]()
Отсюда следует,
что
![]() .
.
выражение для спектральной плотности:
![]() .
.
![]()
С![]() пектральная
плотность функции включения
пектральная
плотность функции включения
![]() .
.
Спектральная плотность:
.![]() .
.
![]()
8. Соотношение неопределённостей в теории сигналов. Из формулы видно, что чем короче сигнал, тем шире его спектр.
База сигнала -произведение длительности сигнала на полосу занимаемых им частот: B=∆f u
Б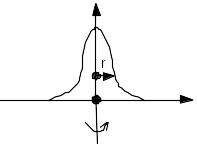 аза
сигнала ограничена снизу. Воспользуемся
методом моментов: найдём центр тяжести,
раскрутим вокруг вертикальной оси и
найдём радиус раскрутки. Два радиуса
раскрутки дают длительность импульса:
аза
сигнала ограничена снизу. Воспользуемся
методом моментов: найдём центр тяжести,
раскрутим вокруг вертикальной оси и
найдём радиус раскрутки. Два радиуса
раскрутки дают длительность импульса:
![]() .
.
Координаты центра тяжести:
![]() .
.
Совместим начало
отсчета с (t0,0)
и составим произведение левых и правых
частей:
![]() Воспользуемся
теоремой Рэлея:
Воспользуемся
теоремой Рэлея:
![]() .
.
Извлечём корень и используем нерав-во Шварца:
![]() .
.
Вычислим скалярное произведение:
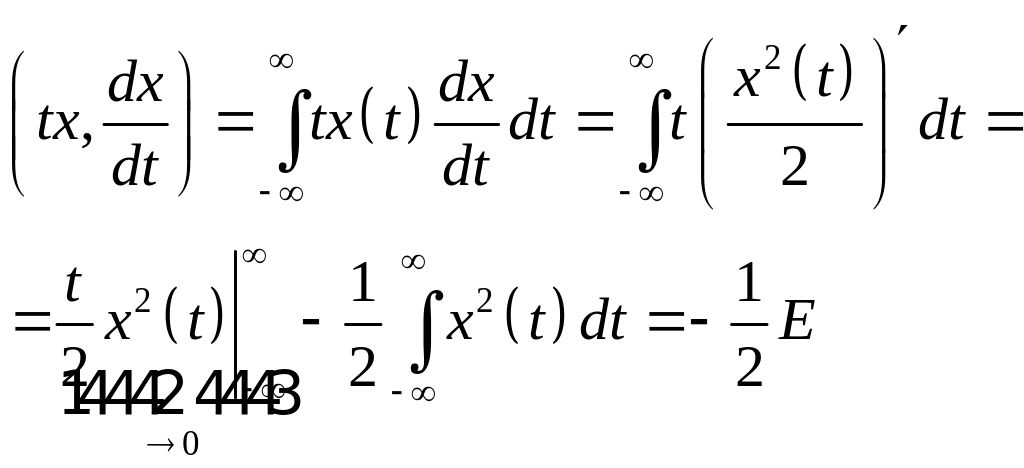
Отсюда следует,
что:![]()
Таким образом база ограничена снизу числом 2. это и есть соотношение неопределённостей в теории сигналов.
Минимальной базой обладает функция Гаусса:
![]() ,
где
,
где
![]() .
.
на практике такой сигнал неосуществим
9 Дискретизация непрерывных сигналов
Дискретизация - замена последовательности значений некоторым дискретным набором.
теорема о выборке гласит, что непрерывный сигнал x(t) полностью определяется своими отсчётами, взятыми с частотой 2Fm, где Fm - верхняя частота спектра. Вводится
![]() ,
шаг дискретизации.
,
шаг дискретизации.
т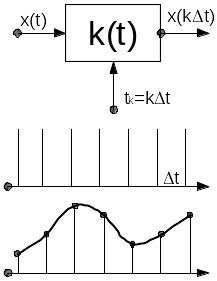 еорема
Котельникова:
Пусть x(t)
- непрерывный сигнал с ограниченным
спектром:
еорема
Котельникова:
Пусть x(t)
- непрерывный сигнал с ограниченным
спектром:
![]() .
Разложим его в обобщённый ряд Фурье:
.
Разложим его в обобщённый ряд Фурье:
![]() ;
;
![]() .
набор базисных ф-ций
.
набор базисных ф-ций
Надо чтобы выполнялась следующая нормировка:
![]() .
.
для обобщённых рядов Фурье можно получить:
И![]() спользуем
условие финитности спектра:
спользуем
условие финитности спектра:
![]() .С
учётом финитности
.С
учётом финитности
![]() ,
а
,
а
![]() .
Последняя формула напоминает обратное
преобразование Фурье. Пусть в диапазоне
частот [-m;m]
спектральная плотность функции φ
постоянна: Sφ=Ф0.
В итоге получится:
.
Последняя формула напоминает обратное
преобразование Фурье. Пусть в диапазоне
частот [-m;m]
спектральная плотность функции φ
постоянна: Sφ=Ф0.
В итоге получится:
![]() .
.
Функция φ(t) с постоянным спектром имеет вид:
![]()
![]() Найдём
теперь скалярное произведение (φk;φm)
:
Найдём
теперь скалярное произведение (φk;φm)
:
Нам надо,
![]()
![]() .
=>
.
=>
![]() .
.
Существует ещё условие ортонормированности:
![]() .
.
Тогда запишем ряд Котельникова в виде:
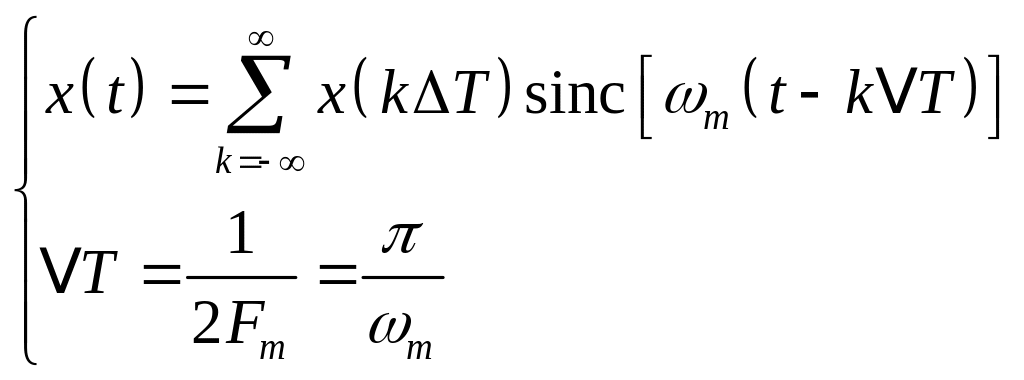 (2.17)
(2.17)
Э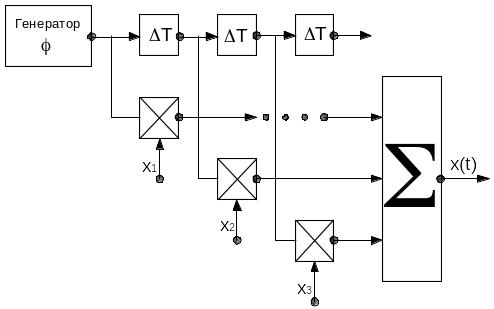 то
и есть теорема Котельникова, позволяющая
сформировать непрерывный сигнал по его
выборке. Замечательность этой теоремы
заключается в том, что сразу ясна
структурная схема устройства, возвращающего
исходный непрерывный сигнал:
то
и есть теорема Котельникова, позволяющая
сформировать непрерывный сигнал по его
выборке. Замечательность этой теоремы
заключается в том, что сразу ясна
структурная схема устройства, возвращающего
исходный непрерывный сигнал:
пример использования теоремы Котельникова:
с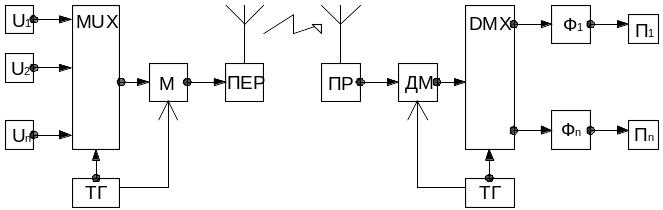 истема
с временным разделением каналов:
истема
с временным разделением каналов:
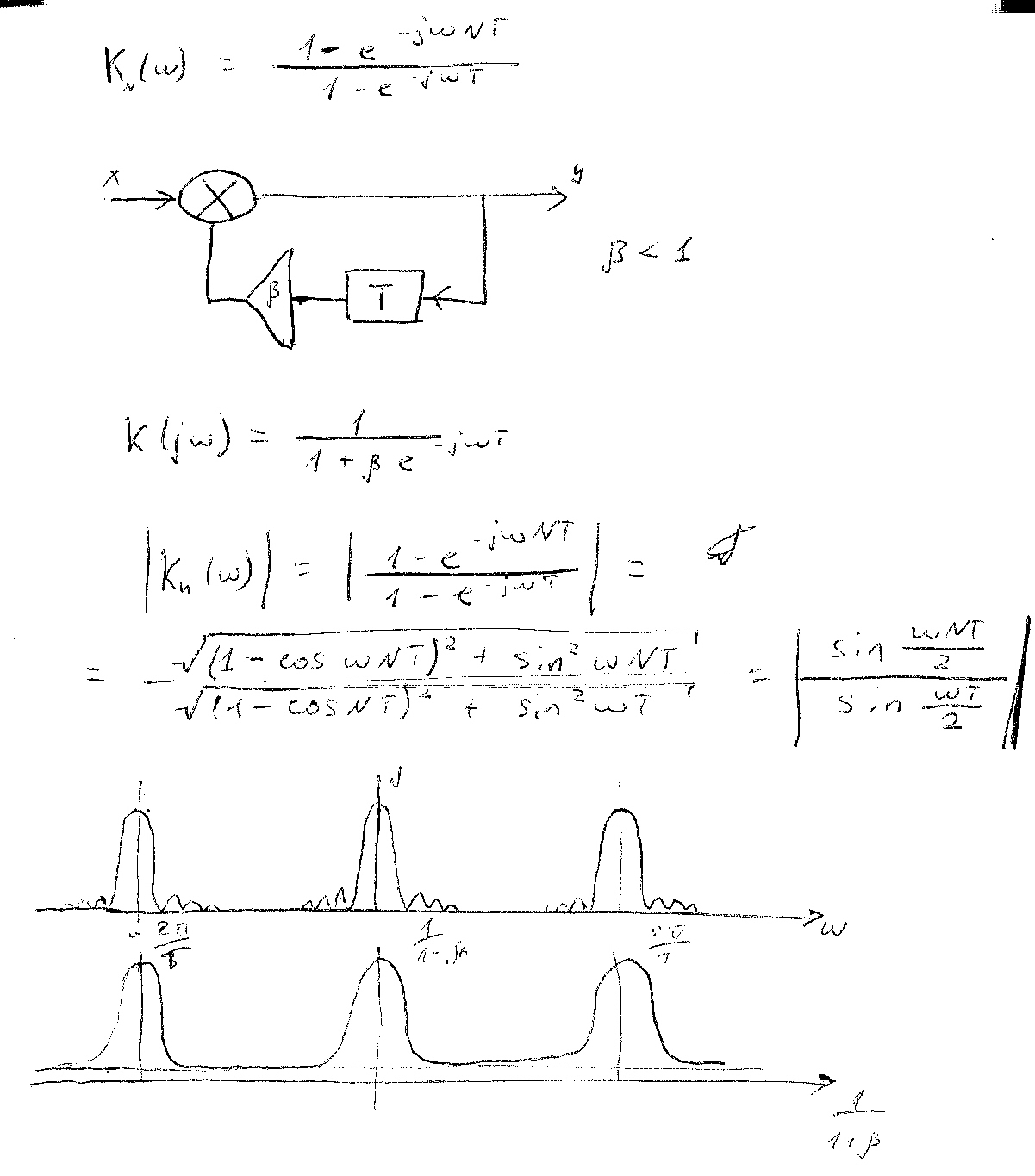
10 дискретизацию можно проводить и в частотной области. Для ограниченного по времени сигнала [0;T] можно производить выборку и по частоте. Формула для частотной выборки:
![]()
Здесь![]()
26.
11. Корреляционный анализ: Kx(0)=Ex;
Для действительных сигналов АКФ чётная:
![]() ;
;
АКФ всегда
ограниченная:
![]() ;
;
АКФ не зависит от сдвига сигналов.
нормировочный коэффициент автокорреляции:
![]()
примеры вычисления АКФ:
1).Сигнал
![]() :
:
АКФ элементарно находится графически. При сдвиге сигнала во времени на , то интеграл будет отличен от нуля там, где наблюдается наложение сигналов. Графиком будет треугольник, ширина основания которого в два раза больше и.
2).Сигнал - радиоимпульс:x(t)=A(t)cos(0t+φ)
![]()
![]() .
.
По лемме Римана
![]()
поэтому:
![]()
для радиоимпульса,
огибающая которого равна
![]() ,
АКФ получится с огибающей в форме
треугольника.
,
АКФ получится с огибающей в форме
треугольника.
3). ЛЧМ сигнал с большой базой ∆fи >>1:
![]()
![]()
![]() ;
;![]() .
.
![]() .
.
найдём функцию автокорреляции:
![]()
![]()
![]() 2-й
интеграл стремится к нулю как интеграл
от быстроосциллирующей функции. Тогда
2-й
интеграл стремится к нулю как интеграл
от быстроосциллирующей функции. Тогда
![]()
используем условие ∆u>>1:
![]()
Г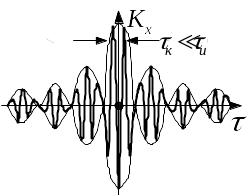 рафик
этой функции на рисунке
рафик
этой функции на рисунке
4) АКФ пачки импульсов
![]() .
.
![]()
с![]()
![]()
![]() уммируем
по диагоналям (j-k)=const.
уммируем
по диагоналям (j-k)=const.
Это приведёт к более простому виду:
![]()
![]() .
.
перепишем так:
![]()
