Федеральное агентство по образованию Российской Федерации

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Аэрокосмический факультет

Кафедра авиационных двигателей и энергетических установок

Курсовая работа

По информационным технологиям

Вариант №3

Выполнили: студенты гр. АД 10

Овчинников Д.С.

Шурубор Д.И.

Проверил: Вятчанин Д. А.

2012

Цель работы: Применение полученных навыков использования расчетного программного продукта MathCad для практических расчетов.

Задание №1. Исследование экстремума функции.

Численные методы оптимизации:

Точки локального минимума и максимума функции f(x) называют точками экстремума этой функции.

Задача отыскания всех локальных минимумов (максимумов) функции f(x), если множество X совпадает со всей числовой прямой, т.е. X = R, называется задачей безусловной оптимизации, а функция f(x) - целевой функцией. Задачу отыскания точек локального минимума целевой функции f(x) символически записывают так: f(x)=min, xϵR Аналогично, задачу отыскания точек локального максимума функции f(x) cимволически записывают следующим образом: f(x)=max, xϵR. Точка x*, в которой первая производная равна нулю, называется стационарной точкой функции f(x).

1. Метод Ньютона.

2. Метод половинного деления.

3. Метод золотого сечения.

4. Метод фибоначчи.

5. Метод сканирования.

Численный метод нахождения экстремумов является метод Ньютона, если метод итераций Ньютона используется для решения уравнения f´(х)= 0. Приведенное к методу итераций уравнение в этом случае представляется в виде:

Итерация-метод последовательных приближений.

Суть метода последовательных приближений состоит в следующем. Начиная с произвольной точки х₀, принадлежащей отрезку [а,b], подставляя х = х₀ в правую часть уравнения x=g(x) получаем

x₁ = g(x₀) - первое приближение.

Подставляя затем х = x₁ в правую часть уравнения x=g(x) получаем

x₂=g(x₁) - второе приближение

…………………………………..

x_k+1=g(x_k)-(k+1)-е приближение,

…………………………………..

Последовательность x₀, x₁, …., x_k,… называется последовательностью итераций для уравнения x=g(x) с начальной точкой х₀.

Последовательность итераций, сходящаяся к решению уравнения f´(x) =0, определяется формулами: _{k=0,1,2,… при условии, что условия сходимости этого процесса выполнены.}

Достаточные условия сходимости последовательности итераций:

1)на концах отрезка производная функции имеет разные знаки, т.е. f´(a)*f´(b)<0;

2)производные второго и третьего порядков f"(x) и f"(x) функции существуют и сохраняют определенные знаки на отрезке [а,b];

3)начальное приближение х0 ϵ [а,b] выбирается так, чтобы знаки производной первого и третьего порядков в точке х0 совпадали, т.е. f´(x0)*f´´´(x0)>0.

Нахождение экстремумов функции нескольких переменных аналогично исследованию функции одной переменной.

Чтобы найти х, при котором путь будет минимальным, нужно найти минимум этой функции. Для поиска экстремумов функции в MаthCad отметим четыре способа:

1. Для непрерывной функции используем равенство нулю производной от заданной функции. В процедуре используется функция root.

2. Для функции с переломами используем функцию miner. Возвращаемый результат зависит от выбора начального приближения.

3. Для ступенчатых функций целесообразно использовать функцию, использовать функции реализующую простой метод перебора значений функции.

4. Для непрерывной функции удобно использовать функции maximize и minimize (они вводятся аналогично функции Find). Ключевое слово Given обычно можно опускать – оно необходимо лишь при наличии ограничений.

Пешеходу необходимо из пункта А добраться до берега реки, а затем перейти в пункт Б, рис. 3. Как проделать этот пункт, пройдя наименьшее расстояние. Расстояние от реки до пункта А а= 1 км, от реки до пункта В в=1,5 км, расстояние между пунктами А и Б с = 3 км.

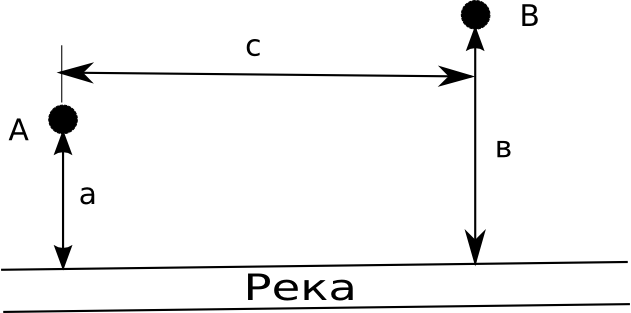
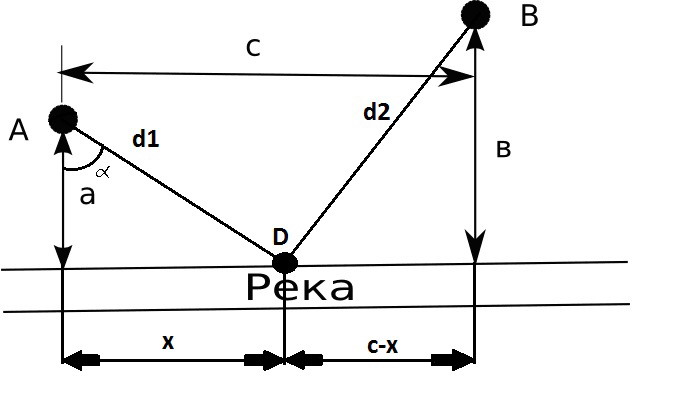
Цель задачи заключается в нахождении угла, под которым пешеход должен отправиться из пункта А к реке, чтобы добраться до пункта В, пройдя наименьшее расстояние. Для этого составим функцию, описывающую движение пешехода. Обозначим точку D реки, к которой придет пешеход, расстояние AD обозначим через d1, расстояние DB через d2. Расстояние с разделим на x и (c-x) соответственно. Из теоремы Пифагора найдем d1 и d2: ; . 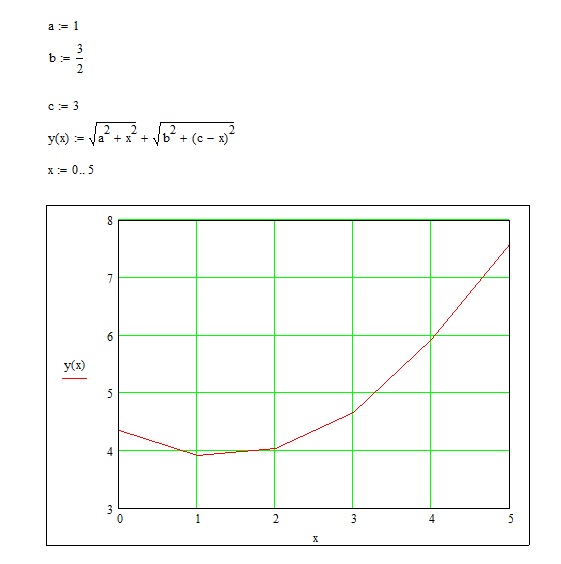Составим уравнение движения пешехода . Найдем такое при котором функция имеет наименьшее значение.

Тогда угол найдется из выражения

Итак:

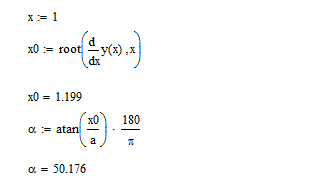
Ответ: задача 1