26. Ряд Фурье по произвольной ортогональной системе функций.
Два сигнала U(t) и V(t) называются ортогональными на промежутке [0,Т] если
.
Пусть мы имеем систему ортогональных функций {U1 ,U2 ,U3, …,Un}
Функции называются ортогональными если
, m≠n
Пусть имеем систему попарно ортогональных функций и функцию x(t) € [0,T]. Запишем ряд Фурье по этой системе функций.
(1) x(t)
=
- ряд Фурье по выбранной системе
произвольно ортогональной системе
функций (базису).
Выразим неизвестные коэффициенты Ci через известную функцию x(t). Возьмем произвольную функцию с номером k. Умножим левую и правую части (1) на функцию Uk(t) и проинтегрируем:
В следствие попарной ортогональности функций системы получим:
Ck
=> Ck
=
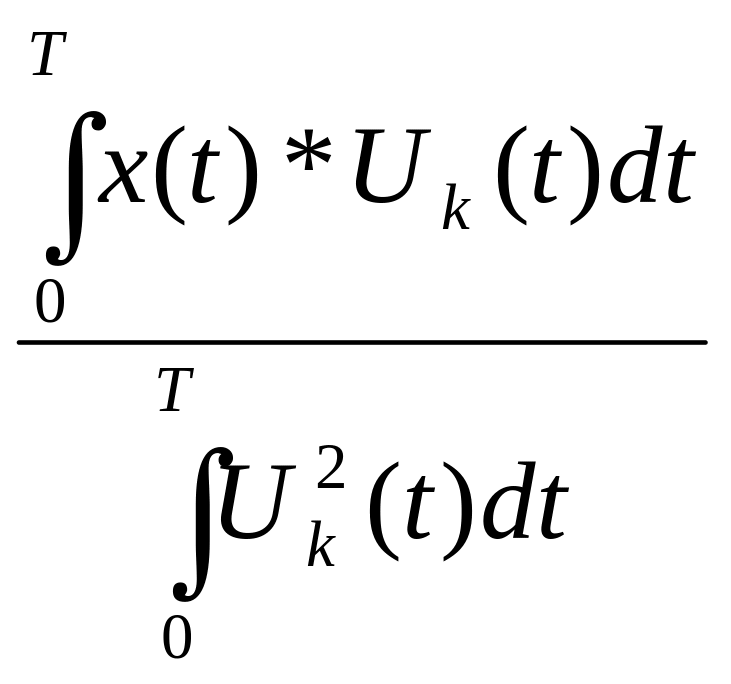- Формула коэффициентов Фурье по
ортогональной системе функций.
- норма функций на
отрезке [0,T]
=> Ck
=
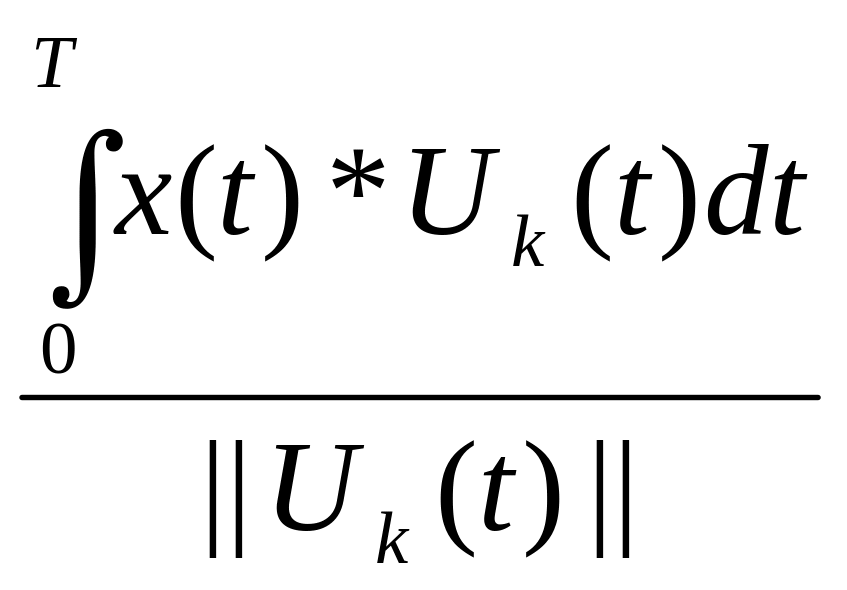
27. Ряд Фурье по основной тригонометрической системе функций.
ОТС: U0 = 1; U1 = sin(w1*t); U2 = cos(w1); U3 = sin(2w1*t)
U4 = cos(2w1*t)
Для того чтобы доказать ортогональность системы функций нужно доказать что:
, m≠n
Ряд Фурье по ОТС:
,
,
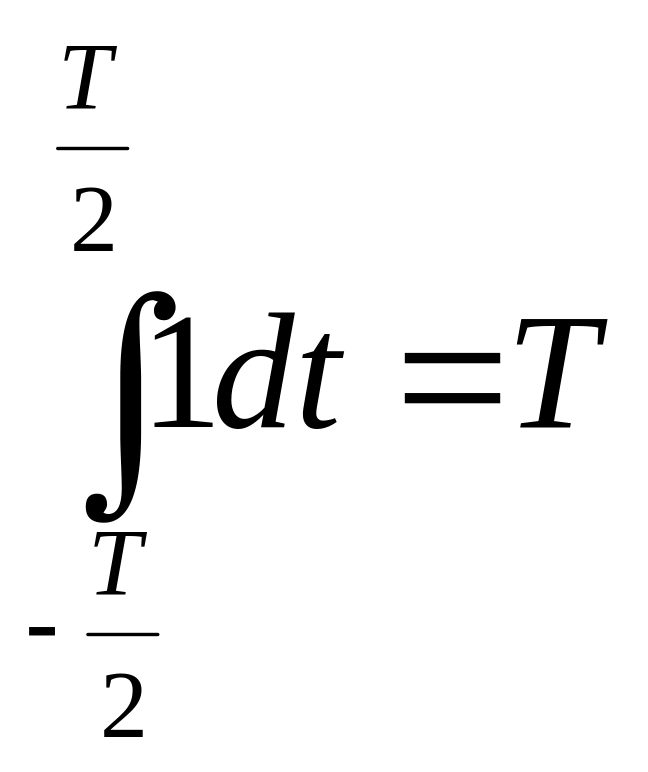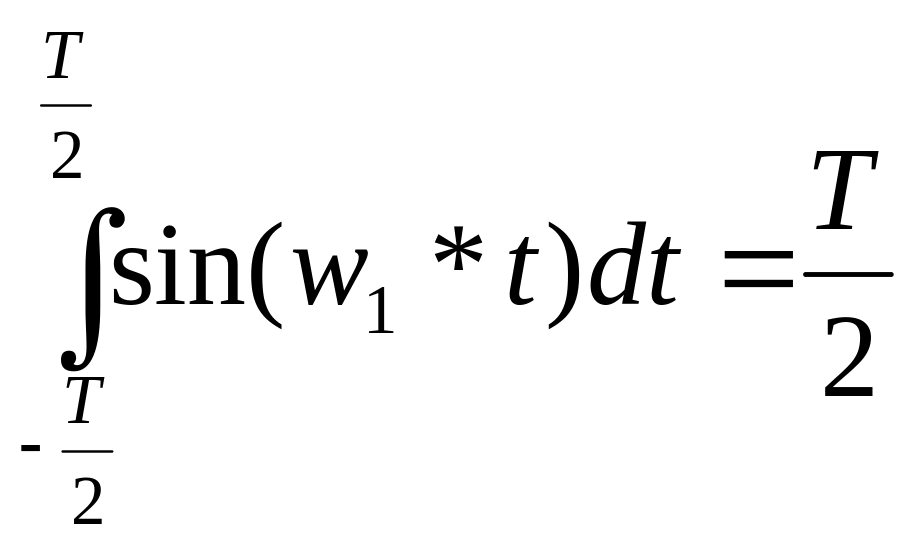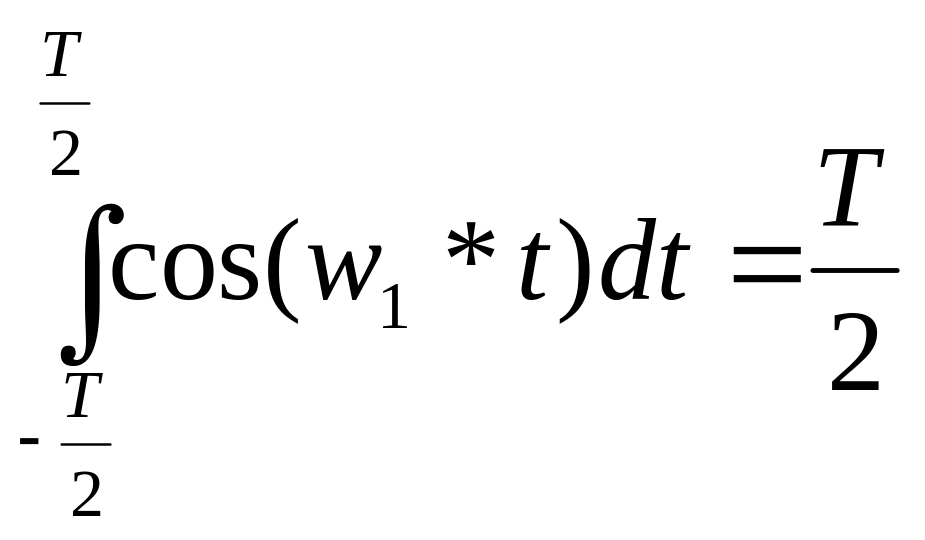
28. Разложение периодических функций в ряд Фурье. Спектр амплитуд и спектр фаз.
Ряд Фурье произвольной периодической функции любого аргумента:
f(x)=
Коэффициент с
номером 0 обозначим
ak = коэффициенты при косинусах
bk = коэффициенты при синусах
ak
=
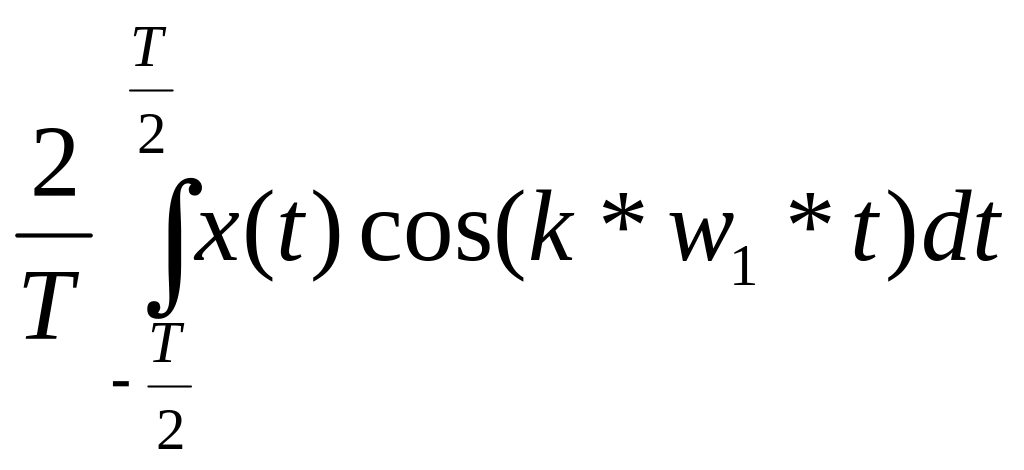
bk
=
,
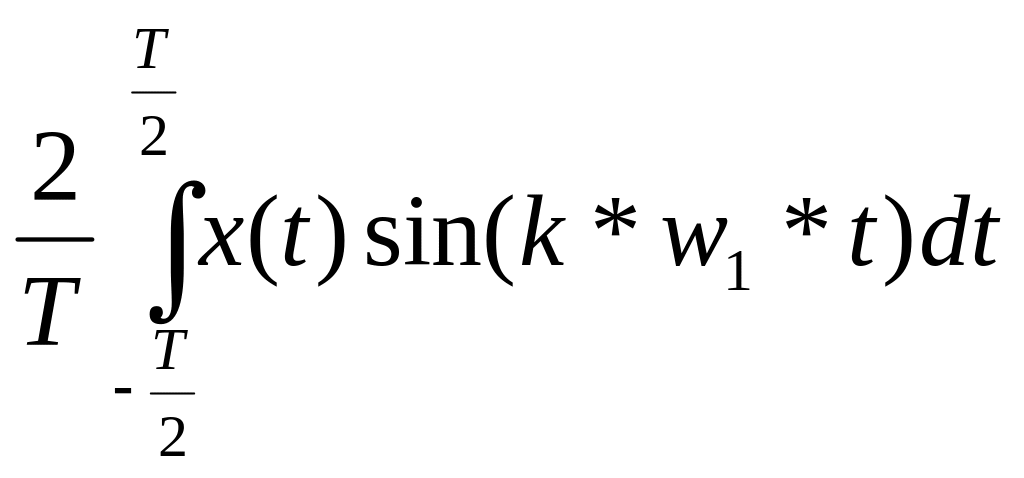
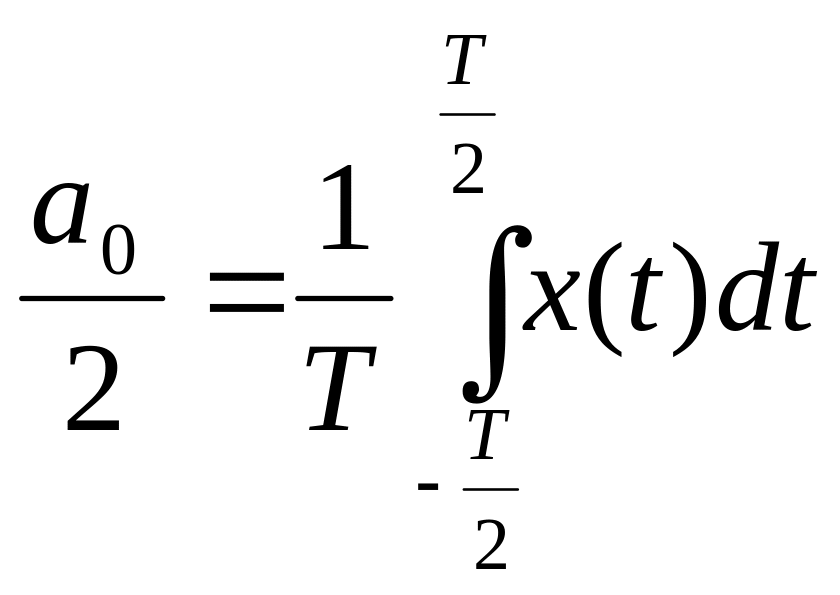w1
=
Множество коэффициентов Фурье – спектр
Ak
=
x(t)=
- Ряд Фурье в тригонометрической форме
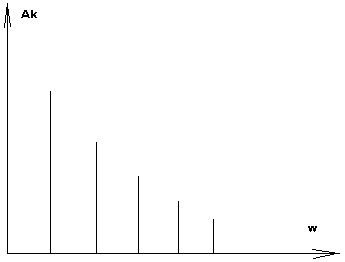
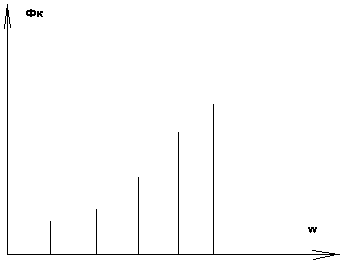
Тригонометрический базис инвариантен к сдвигу. Спектры по периоду Т1 и Т2 совпадают.
Тригонометрический базис является мощным средством и инструментом описания сигналов и анализа систем.
29. Ряд Фурье в комплексной форме. Спектр фаз и спектр амплитуд.
=
,
т.к.
- Ряд Фурье в
комплексной форме
, где
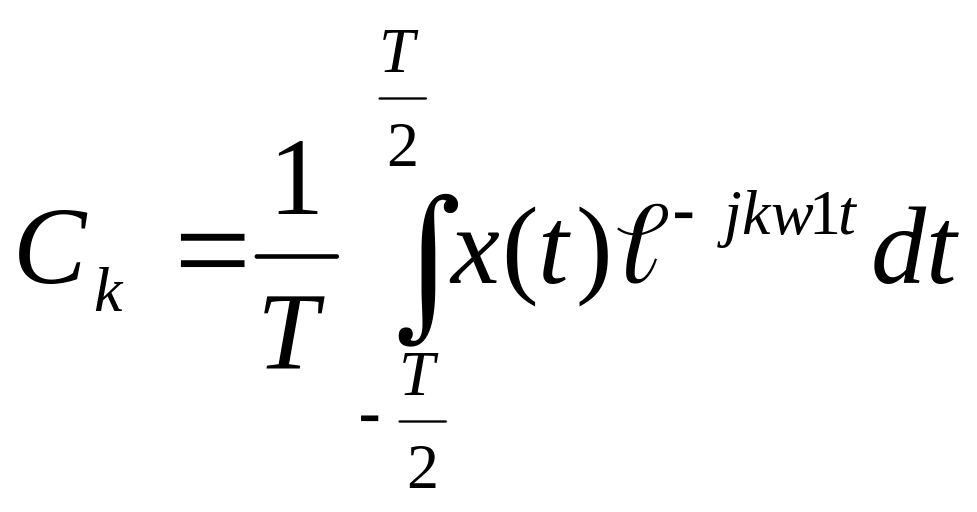
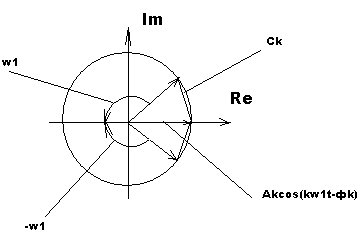
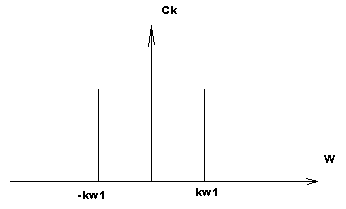
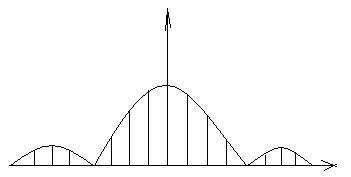
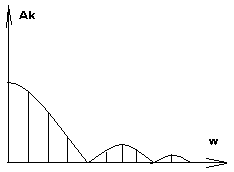
Отрицательные частоты в комплексном спектре понятие не физическое, а математическое, как следствие представления комплексных чисел.
30. Спектр мощности сигнала. Практическая ширина спектра. Равенство Парсеваля. (3 стр!!!)
- Энергия, где u(t)
– напряжение, i(t)
– сила тока.
- Энергетический
спектр.
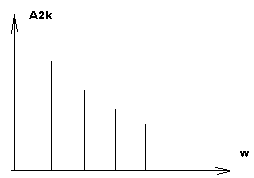
P=u(t)*i(t),
P=
- мощность
- Прямое преобразование Фурье (спектральная
плотность мощности).
-
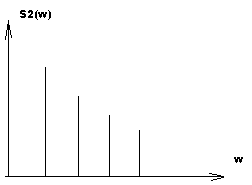
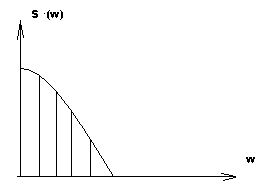
Равенство Парсеваля – энегрия рассеиваемая
на 1-ом Оме.
Практическая ширина спектра.
Периодический сигнал: x(t)= ,
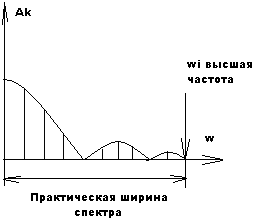
На практике передаваемые по каналу не могут быть переданы с очень высокими частотами т.к. реальные системы имеют ограниченную частоту пропускания (ограниченная частотная характеристика).
Обычно используют два критерия для выбора высшей частоты спектра.
1. Критерий, в основе которого лежит выбор частоты, которая обеспечивает передачу сигнала заданной мощности. Каждая гармоника несет свою долю мощности. Вся мощность сигнала:
=> число;
=> функция
λ
=
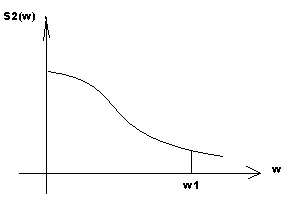
2. Критерий основанный на соображениях формы сигналов. Важно не сохранение мощности сигнала, а его форма.
Равенство Парсеваля.
- Энергия, где u(t) – напряжение, i(t) – сила тока.
- Энергетический спектр.
P=u(t)*i(t), P= - мощность
- Прямое преобразование Фурье (спектральная плотность мощности).
- Равенство Парсеваля – энегрия рассеиваемая на 1-ом Оме.
31. Спектральные характеристики непериодического сигнала. Прямое и обратное преобразования Фурье.
Пусть имеется одиночный сигнал, наблюдаемый на времени Т.
Устремим Т --> ∞, тогда соседние спектре могут стать сколь угодно близкими друг к другу. Дискретную переменную kw1 можно заменить переменной w текущей частоты, тогда суммы преобразуются в интеграл:
,
где
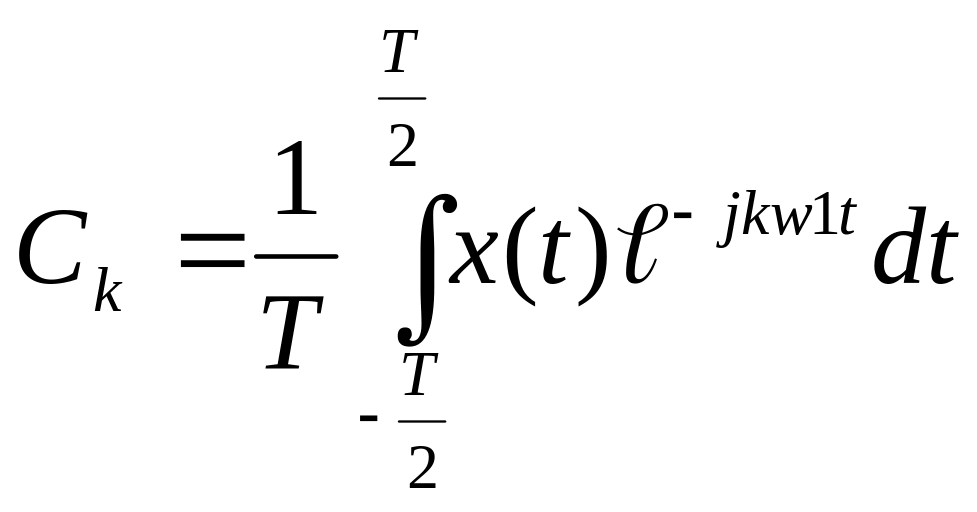
- Прямое преобразование Фурье (спектральная плотность мощности).
Физический смысл спектральной плотности мощности – комплексная функция частоты одновременно является несущей информацию об амплитуде и фазе элементарных синусоид.
х(t)
=
- Обратное преобразование Фурье.