12 Сущность и значение теоремы Чебышева. Теорема Бернулли.

Неравенство:Если случайная величина Х имеет конечные математическое ожидание М(Х) и дисперсию Д(Х), то для любого положительного e справедливо неравенство

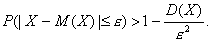Теорема Чебышева: При достаточно большом числе независимых случайных величин Х1, Х2, Х3, ..., Хn, дисперсия каждой из которых не превышает одного и того же постоянного числа В, для произвольного сколько угодно малого числа e справедливо неравенство

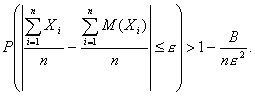Среднее арифметическое случайной величины Х обладает свойством устойчивости. Теорема позволяет, используя среднее арифметическое, получить представление о величине математического ожидания, и наоборот.

Теорема Бернулли: Если вероятность события А в каждом из п независимых испытаний постоянна и равна р, то при достаточно большом п для произвольного e >0 справедливо неравенство Переходя к пределу, имеем Теорема Бернулли устанавливает связь между вероятностью появления события и его относительной частотой появления и позволяет при этом предсказать, какой примерно будет эта частота в п испытаниях. Из теоремы видно, что отношение т/п обладает свойством устойчивости при неограниченном росте числа испытаний

13. Функция распределения: определ.,св-ва, график

Функцией распределения называют функцию F (х), определяющую для каждого значения х вероятность того, что случайная величина X

примет значение, меньшее х, т. е. F(x) = P(X < x).

Функция распределения обладает следующими свойствами:

Св-во 1. Значения функции распределения принадлежат

отрежу [0; 1]:

0 ≤ F(x) ≤ 1.

Св-во 2. Функция распределения есть неубывающая функция: F(x2) ≥ F(x1), если х2 > х1.

Следствие 1. Вероятность того, что случайная величина X

примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:

Р(а < X < b) = F(b) - F(a).

Следствие 2. Вероятность того, что непрерывная случайная

величина X примет одно определенное значение, например хи равна нулю: Р (X = x1) =0.

Свво 3. Если все возможные значения случайной вели-

чины X принадлежат интервалу (а, b), то

F(x) = 0 при х ≤ а; F(x) = l при x ≥ b

Следствие. Справедливы следующие предельные соотношения: lim F(x) = 0, lim F(x) = 1

x стрем.к –бесконеч х стрем.к +бесконеч

Св-во 4. Функция распределения непрерывна слева:

lim F(x) = F(x0).

x↑x(r)

14. Плотность распределения вероятностей: опред.Св-ва, вероятностный смысл.Вероятность попадания непрерывной случ.Величины в заданной интервал

Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f(x) = F' (х).

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), определяется равенством ь

P (а < Х < b) = $f(x)dx. ($-знак интеграла от a до b)

Зная плотность распределения, можно иайти функцию распределения F(x) = $ f(x)dx.

($ - знак интеграла от –бесконеч. до х)

Плотность распределения обладает следующими свойствами:

Св-во 1. Плотность распределения неотрицательна, т. е.

f(x) ≥ 0

Св-во 2. Несобственный интеграл от плотности распределения в пределах от -∞ до ∞ равен единице: $f(x)dx = l. ($ - интеграл от –беконеч.до +бесконеч)

В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то $ f(х)dx = l. ($ - интеграл от a до b)

19 Оценка генеральной средней по выборочной средней.В качестве оценки генеральной средней принимают выборочную среднюю *В=(*1+ *2+•• Тем самым доказано, что выборочная средняя есть несмещенная оценка генеральной средней.Легко показать, что выборочная средняя является и состоятельной оценкой генеральной средней.Итак, при увеличении объема выборки п выборочная средняя стремится по вероятности к генеральной средней, а это и означает, что выборочная средняя есть состоятельная оценка генеральной средней.Она зависит от объема выборки: чем объем выборки больше, тем меньше выборочная средняя отличается от генеральной. Устойчивость выборочных средних-если имеются несколько выборок большого объема из одной генеральной совокупности их средние будут приближенно будут равны между собой.Групповая и общая средние:Допустим, что все значения количественного признака X совокупности, безраз-лично - генеральной или выборочной, разбиты на несколько групп.Рассматривая каждую группу как самостоятельную совокупность, можнонайти ее среднюю арифметическую. Групповой средней называтся среднее арифметическоезначений признака,принадлежащих группе. Теперь целесообразно ввести специальный термин для средней всей сово-купности.Общей средней x называется среднее арифметическое зна-чений признака, принадлежащих всей совокупности.Зная групповые средние и объемы групп, можно найти общую среднюю:общая средняя равна средней арифметической групповых средних, взвешеннойпо объемам групп.Отклонение от общей средней и его свойство- безразлично-генеральную или выборочную,значений количественного признака X объема n:значения признака x1 x2 . . . xk частоты n1 n2 . . . nk.При X( знак суммы) от k до i=1 ni = n. Найдем общую среднюю: x(средняя) =1/n X от k до i=1 nixi . Отсюда.Xот k до i=1 nixi = nx(средняя).Отклонением называют разность xi − x между значениемпризнака и общей средней. Можно показать, что cумма произведений отклонений на соответствующие частоты равна нулю:Xk i=1 ni(xi − x) = Xk i=1 nixi – Xk i=1 nix = nx − nx = 0. Это означает: среднее значение отклонения равно нулю.

20 Генеральной дисперсией называют среднее арифметическое квадратов отклонений значений генеральной совокупности от их среднего значения.

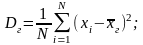
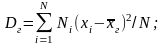
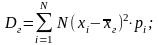
К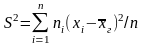 роме дисперсий для характеристики рассеивания значений генеральной совокупности вокруг своего среднего пользуются другой характеристикой – средним квадратическим отклонением. Выборочной дисперсией называют среднее арифметическое квадратов отклонений наблюдаемых значений выборки от их среднего значения.

– с повторениями.Для оценки рассеивания выборки служит выборочное среднеквадратическое отклонение.

 Точечные оценки параметров распределения. - статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин. Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.