6. Формула Бернули. Локальная и интегральная теоремы Лапласа. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях. Формула Бернули.

Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна p^kq^n-k. Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. C^k_n. Так как эти сложные события несовместны, то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженной на их число:

Р_n(k) = C^k_np^kq^n-k

или P_n(k)=____n!____p^kq^n-k

k!(n-k)!

Полученную формулу называют формулой Бернулли.

Локальная теорема Лапласа.

Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р_n(k) того, что событие А появиться в n испытаниях ровно k раз, приближенно равна значению функции

при x =(k – np)/ .

Вероятность того, что событие А появится в n независимых испытаниях ровно k раз, приближенно равна

P_n(k) ≈˜ 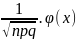где, x=(k-np)/ .

Интегральная теоремы Лапласа.

ТЕОРЕМА. Если вероятность p наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k_1,k₂) того, что событие А появится в n испытаниях от k₁ до k₂ раз, приближенно равна определенному интегралу

P_n(k₁,k₂)~ _1_ ∫^x_xe^-z2/2dz, (*)

где х^!=(k₁ – np)/ и х^!!=(k₂ – np)/ .

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл не выражается через элементарные функции.

Для того, чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (*) так:

Итак, вероятность того, что событие А появится в n независимых испытаниях от k₁ до k₂ раз,

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

Производится n независимых испытаний в каждом из которых вероятность появления события А постоянна и равна р (0<р<1). Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты m/n от постоянной вероятности р по абсолютной величине не превышает заданного числа ε > 0. Другими словами, найдем вероятность осуществления неравенства |m/n - p|≤ ε (*)

Эту вероятность будем обозначать так: Р(|m/n - p|≤ ε).

Заменим неравенство (*) ему равносильными:

-ε≤ m/n - p≤ ε или -ε≤ (m – np)/п≤ ε.

Умножая эти неравенства на положительный множитель , получим неравенства равносильные исходному:

-ε ≤(т-пр)/ ≤ε .

Воспользуемся интегральной теоремой Лапласа

Наконец, заменив неравенства, заключенные в скобках, равносильным им исходным неравенством, окончательно получим

Р(|m/n - p|≤ ε)~2Ф(ε ). Вероятность осуществления неравенства |m/n - p|≤ ε приближенно равна значению удвоенной функции Лапласа 2Ф (х) при х = ε .

7.Под случайной величиной понимается переменная , которая в результате испытания в зависимости от случая принимает одного из возможного множества своих значений.

Виды случайных величин:

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:

x			…..	xn
p			......	pn

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события образуют полную группу; следовательно, сумма вероятностей этих событий, т.е. сумма вероятностей второй строки таблицы, равна единице:

Если множество возможных значений бесконечно (счетно), то ряд сходится и его сумма равна единице.

Графическое представление этой таблицы называется многоугольником распределения. По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности.

Случайная величина X имеет биномиальное распределение с параметрами n и m, если она принимает значения 0,1, ... n с вероятностями:

где q = 1 — p, a — биномиальные коэффициенты (отсюда название Б. р.). Приведённая формула иногда называется формулой Бернулли.

8.Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (О < р < 1) и, следовательно, вероятность его не появления q = 1 - р. Испытания заканчиваются, как только появится событие А (т.е. количество испытаний неограниченно). Таким образом, если событие А появилось в k-м испытании, то в предшествующих k—1 испытаниях оно не появлялось.

Обозначим через X дискретную случайную величину - число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями Х являются натуральные числа: 1, 2, 3…

Пусть в первых k—1 испытаниях событие А не наступило, а в k-м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий,

Полагая k=1, 2, ... в формуле , получим геометрическую прогрессию с первым членом р и знаменателем q

По этой причине распределение называют геометрическим.

Легко убедиться, что ряд сходится и сумма его равна единице. Действительно, сумма ряда есть сумма членов бесконечной геометрической прогрессии со знаменателем меньшим единицы, тогда сумма его :

если количество испытаний ограничено каким- либо натуральным числом k , то последнее значение вероятности в ряде распределения будет равно qk-1 , означающее, что в предыдущих k-1 испытаниях событие А не появилось.

Дискретная случайная величина Х имеет гиппергеометричекое распределение, если она принимает значения. 1,2,3…..m.in(n. M) c вероятностями

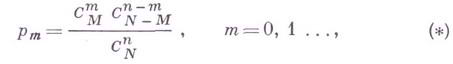
где М, N и n - целые неотрицательные числа и ,

математическое ожидание случайной величины Х, имеющей гипергеометрическое распределение с параметрами n, M.

Математическое щжидание случайной величины Х, имеющей гипергеометрическое распределение с параметрами n, M,N есть M(X)= n*M/N, а ее дисперсия D(X)= n*M/n-1*(1-M/N)*(1-n/N)

Распределение Пуассона - это дискретное распределение , являющееся одним из важных предельных случаев биномиального распределения. При росте n и зафиксированном значении произведения np=λ > 0 биномиальное распределение B(n,p) сходится к распределению Пуассона . Таким образом, случайная величина, имеющая распределение Пуассона с параметром λ, принимает неотрицательные целые значения с вероятностью

Интегральная функция вероятности распределения равна

Параметр λ является одновременно и математическим ожиданием, и дисперсией случайной величины, имеющей распределение Пуассона .

Примером случайной величины, распределенной по Пуассону , является количество машин, проезжающих через какой-либо участок дороги за заданный период времен. Также можно отметить такие примеры, как количество звезд на участке неба заданной величины, количество ошибок в тексте заданной длины или количество обращений к веб-серверу за заданный период времени.

9.

Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности: M(X) = x₁p₁ + x₂p₂ + ... + x_np_n

Свойства математического ожидания. 1) Математическое ожидание постоянной величины равно самой величине:М(С) = С 2) Постоянный множитель можно выносить за знак математического ожидания:М(СХ) = С·М(Х) 3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых: М(Х₁ + Х₂ + …+ Х_n) = М(Х₁) + М(Х₂) + ... + М(Х_n) 4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей: М(Х₁ · Х₂ · ... · Х_n) = М(Х₁) · М(Х₂) · ... · М(Х_n)

Теорема. Математическое ожидание числа появления события в независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.

10

Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(X) = M(X²)- [M(X)]²=(x₁ - M(X))²p₁ + (x₂ - M(X))²p₂ + ... + (x_n- M(X))²p_n = x²₁p₁ + x²₂p₂ + ... + x²_np_n - [M(X)]²

Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х₁ ± Х₂ ± ... ± Х_n) = D(Х₁) + D(Х₂) + ... + D(Х_n)

Теорема. Дисперсия числа появлений события A в n независимых испытаниях, в каждом из которых вероятность p события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании.D (X)=npq

11. Серднее квадратическое отклонение. Ср.квадрат-е отклонение суммы взаимно независимых случайных величин.Одинаково распределенные взаимно независимые случайные величины.Начальные и центральные теоретические моменты.

Определение. Средним квадратическим отклонением  случайной величины Х называется квадратный корень из дисперсии.

Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.

Среднее квадратичное отклонение принято обозначать греческой буквой сигма σ:

Если число измерений примерно равно 10, то истинное значение величины может отличаться от среднего арифметического не более чем на величину среднего квадратичного отклонения σ. Отклонения, большие, чем σ, возможны лишь в исключительных случаях, число которых составляет около 0.5% всех возможных случаев.

Если число измерений значительно больше десяти, то максимальное практически возможное отклонение истинной величины от среднего арифметического будет меньше чем σ. Отклонение не превысит значения: ▲=3 σ/ √n.

Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в   раз меньше среднего квадратического отклонения каждой величины:( Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных и Дисперсия среднего арифметического)

σ (Х) = σ/√n

Таким образом, среднее арифметическое достаточно большого числа взаимно независимых случайных величин имеет значительно меньшее рассеяние, чем каждая отдельная величина. С увеличением n величина   почти перестает быть случайной и приближается к постоянной М. Тем самым оправдывается рекомендуемый в практической деятельности способ получения более точных результатов измерений: одна и та же величина измеряется многократно, и в качестве ее значения берется среднее арифметическое полученных результатов измерений. Начальные и центральные теоретические моменты.

Начальным моментом порядка k случайной величины X называют математическое ожидание величины X^k:

Центральным моментом порядка k случайной величины X называют математическое ожидание величины (X—M(X))^k:

Моменты, рассмотренные здесь, называют

теоретическими. В отличие от теоретических моментов, моменты которые вычисляются по данным наблюдений, называют эмпирическими.