30. Квадратурные формулы Ньютона-Котеса.

Основная идея – замена подынтегральной функции интеполяционный полином Лагранжа.

, при этом узлы берутся равноудаленными

xi	x0	x1	…	xn
yi	y0	y1	…	yn

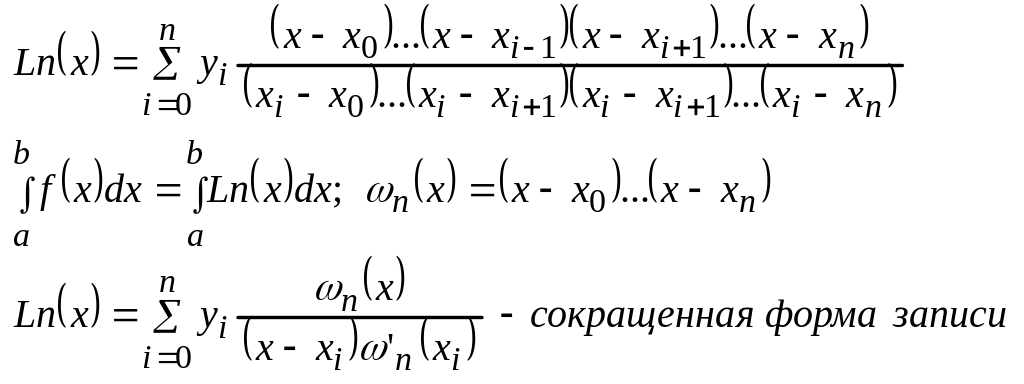
Тогда

Если предположить, что интеграл сходящийся, то в правой част последней формулы можно поменять местами операции интегрирования и суммирования. Сделав это, мы получаем .

A_i – коэффициент Ньютона Котеса

Далее

-квадратурная формула Ньютона – Котесса

Используя теорему об оценки погрешности ИПЛ можно вывести (получить) неравенство для оценки погрешности квадратурной формулы R(f). Рассмотренные ранее формулы трапеции и параболы явл-ся частным случаем КФНК, соответственно при n=1 и n=2.

Частный случай.

n=1

xi	x0	x1
yi	y0	y1

x₀=a x₁=b h=b-a

В этом случае формула (1) принимает вид

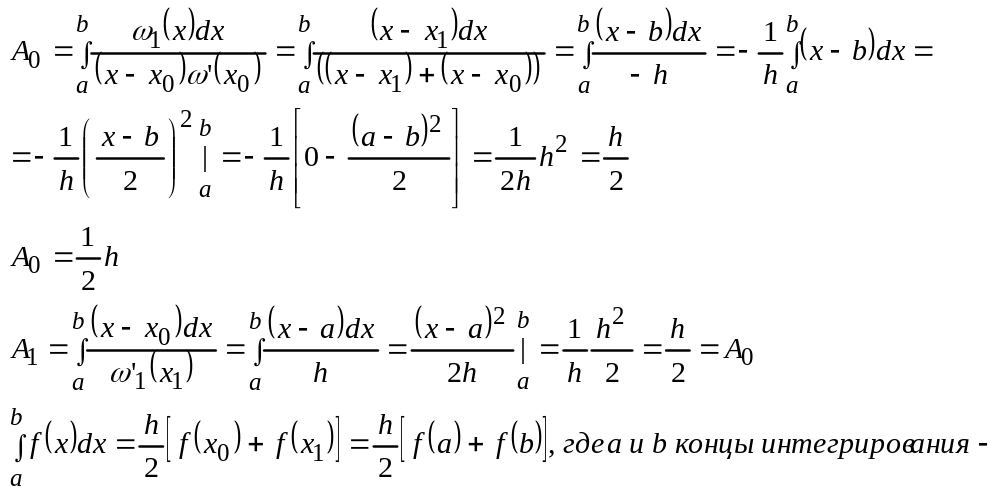
малая формула трапеций.

n=2

xi	x0	x1	x2
yi	y0	y1	y2

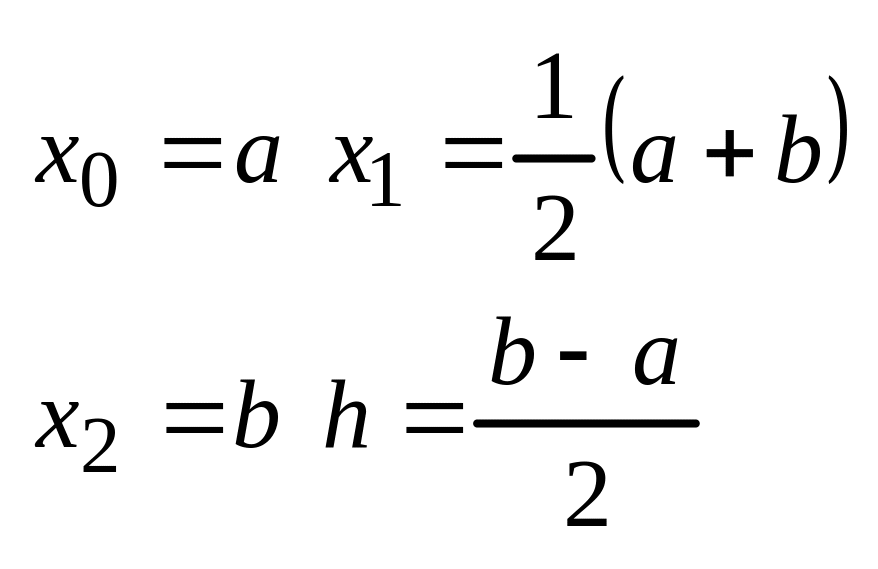
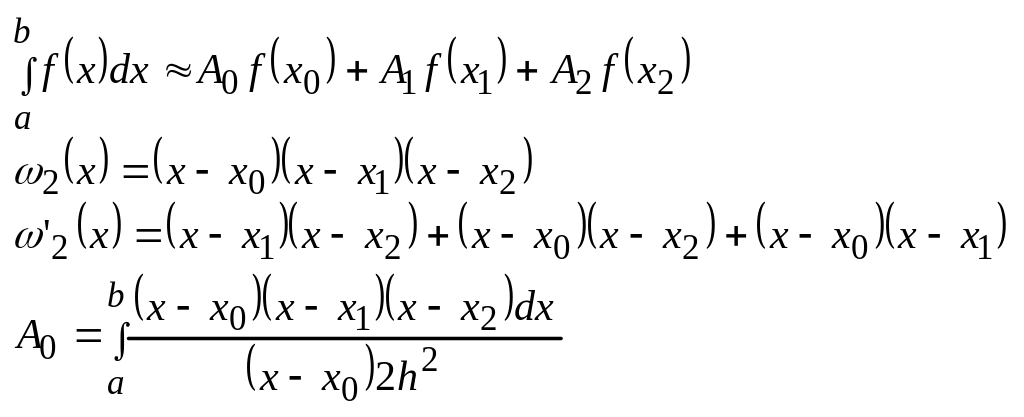
31. Задача Коши для обыкновенного дифференциального уравнения (оду) 1 порядка. Метод Эйлера.

Большинство дифференциальных уравнений, возникающих на практике точно решить не удается, для их решения применяют приближенные или численные етоды.

Приближенный метод позволяет найти решение задачи в виде некоторой функции от x . Используя полученную ф-ю при необходимости можно определить числовые значения искомого решения.

Численный метод позволяет найти решение задачи в виде совокупности числовых значений искомого решения в заранее определенных узловых точках.

Преимуществом числовых численных методов яв-ся то, что они легко программируются, поэтому находят большее применение на рпактике.

Пусть дана задача Коши для обыкновенного дифференциального уравнения I порядка:

Теорема о существовании и единственности решения задачи.

Если ф-я f(x,y) непрерывная по обеим переменным, то существует ограниченная частная производная в рассматриваемой области то решение задачи (1)-(2) существует и яв-ся единственным.

Рассмотрим численные методы решения этой задачи.

Метод Эйлера

Допустим, что интегральная кривая известна. Отрезок [a;b] разобьем на n-равных частей точками x_i.

, проведем прямые x=x_i, которые заключены между интегральной кривой и осью абсцисс на участке [x₀;x₁]интегральная кривая, приближенно заменяется касательной к кривой, проведенной через точку A₀. На остальных участках [x₁;x₂], [x₂;x₃], и т.д. интегральная кривая приближенно заменятся прямой, параллельной касательной.

1способ. Напишем Ур-е касательной к интегральной кривой в точке A₀.

Найдем ординату точки A₁, для этого вместо x поставим x₁: . Используя исходное уравнение и начальное условие, последнее можем переписать (координата точки А₁).

На остальных участках рассуждение почти аналогичны.

….

Если отрезок [a;b] большой, то полученное решение может сильно отличаться от точного решения.

Погрешности метода.

Запишем расположение фун-ии y(x) в ряд Тейлора

Опр. Говорят, что ф-ия яв-ся величиной . , если существует константа С такая, что

В разложении (5) отбросим вс слагаемые, содержащие h²,h³, и т.д.

Обозначим x=x_i, x+h=x_i+1, используя исходное ур-е (7) перепишм

Сравним (4) и (8), заключаем, что на произвольном элементарном участке погрешность формулы (4) составляет величину O(h²). Определим погрешность на всем отрезке [a;b] nO(h²), из определения следует, что O(h²) – линейная, т.е.

На всем отрезке [a;b] погрешность пропорциональна h.

Метод Эйлера имеет самый низки порядок точности по h. Метод Эйлера яв-ся грубым, поэтому его обычно применяют для выявления хар-ра интегральной кривой. На практике стараются использовать более точные методы.