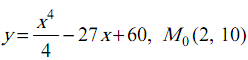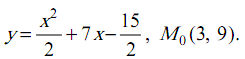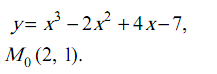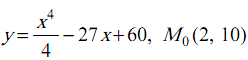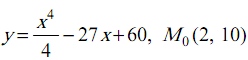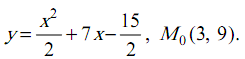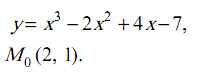1320_21_22_kr_1_sem
.docКонтрольная работа для студентов заочного отделения,
группы 1320, 1321, 1132.
(2013/2014 уч.год, осенний семестр)
Преподаватель: к.п.н, доцент Т.Г. Макусева
Указания по выполнению контрольной работы.
1. На обложке тетради необходимо написать фамилию, имя, отчество, курс, группу, вариант контрольной работы и дату сдачи ее в институт.
2. Решение задач располагать в порядке номеров, указанных в заданиях, сохраняя их номер.
3. Перед решением каждой задачи выписать полностью условие.
4. Решение каждой задачи сопровождать объяснениями и заканчивать ответом.
5. Оформление решений производить аккуратно, с минимальным количеством исправлений. Оставить поля для замечаний проверяющего.
Контрольная работа.
Задача 1. Найти предел функции.
1. а)
![]() , б)
, б)
![]() в)
в)
![]()
2.
![]() , б)
, б)
![]() в)
в)
![]()
3.
![]() , б)
, б)
![]() в)
в)
![]()
4.
![]() , б)
, б)
![]() , в)
, в)
![]()
5.
![]() , б)
, б)
![]() , в)
, в)
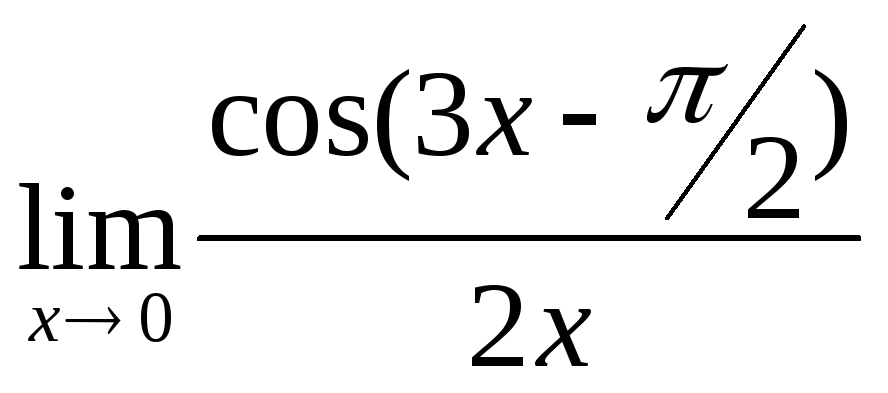
6.
![]() , б)
, б)
![]() , в)
, в)
![]()
7.
![]() ,
б)
,
б)
![]() , в)
, в)
![]()
8.
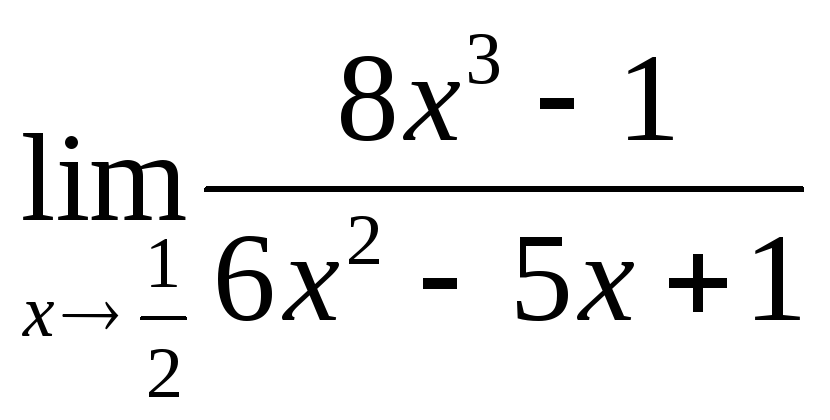 ,
б)
,
б)
![]() , в)
, в)
![]()
9.
![]() , б)
, б)
![]() ,
в)
,
в)
![]()
10.
 б)
б)
![]() в)
в)
![]()
11. а)
![]() , б)
, б)
![]() в)
в)
![]()
12.
![]() , б)
, б)
![]() в)
в)
![]()
13.
![]() , б)
, б)
![]() в)
в)
![]()
14.
![]() , б)
, б)
![]() , в)
, в)
![]()
15.
![]() , б)
, б)
![]() , в)
, в)
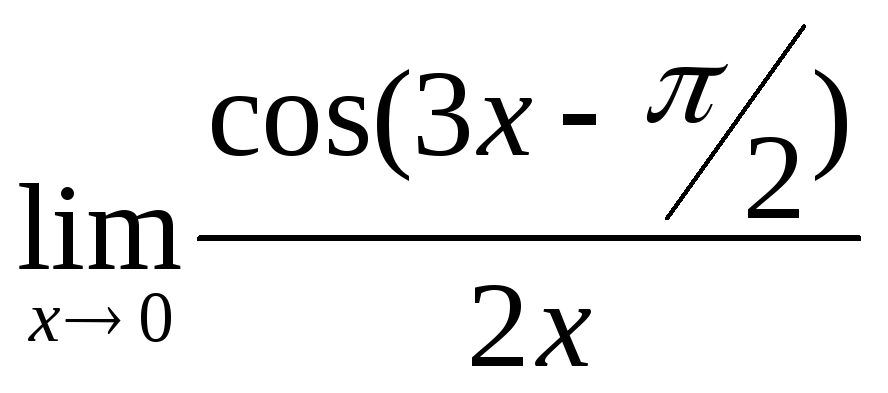
16.
![]() , б)
, б)
![]() , в)
, в)
![]()
17.
![]() ,
б)
,
б)
![]() , в)
, в)
![]()
18.
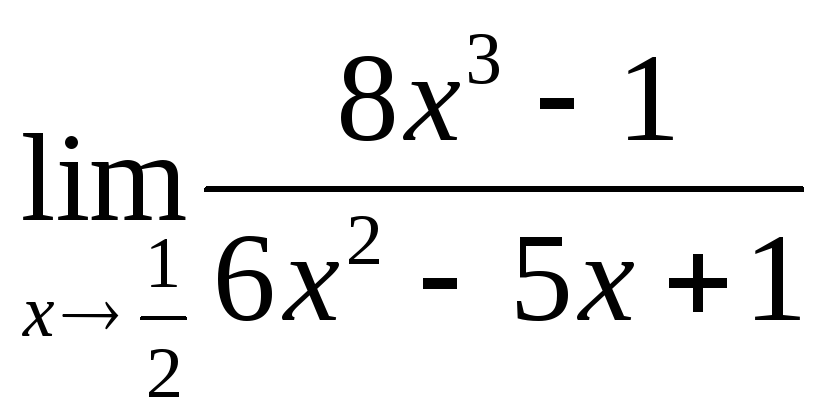 ,
б)
,
б)
![]() , в)
, в)
![]()
19.
![]() , б)
, б)
![]() ,
в)
,
в)
![]()
20.
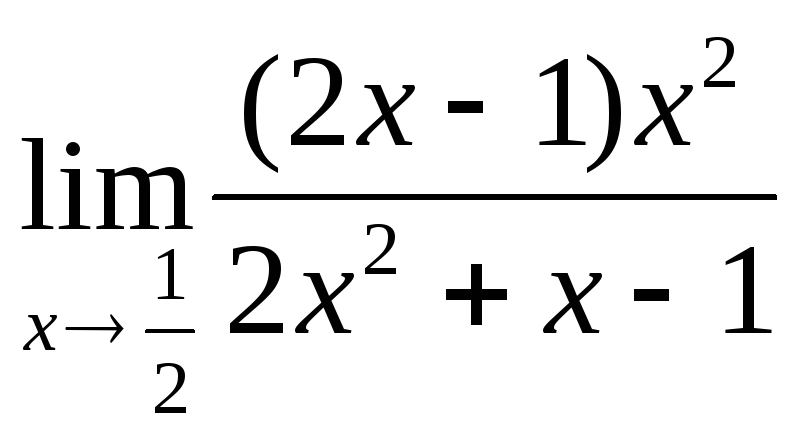 б)
б)
![]() в)
в)
![]()
Задача 2. В задачах 1–20 найти производные функций.
1. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
2. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
3. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
4. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
5. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
6. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
7. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
8. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
9. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
10. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
11. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
12. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
13. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
14. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
15. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
16. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
17. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
18. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
19. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
20. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
21. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
22. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
23. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
24. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
25. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
26. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
27. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
28. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
29. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
30. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
.
Задача 2. В задачах исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы возрастания и убывания функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.
1.
![]() . 2.
. 2.
![]() . 3.
. 3.
![]() .
.
4.
![]() . 5.
. 5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() . 9.
. 9.
![]() .
.
10.
![]() . 11.
. 11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() . 15.
. 15.
![]() .
.
16.
![]() . 17.
. 17.
![]() . 18.
. 18.
![]() .
.
13.
![]() . 14.
. 14.
![]() . 15.
. 15.
![]() .
.
16.
![]() . 17.
. 17.
![]() . 18.
. 18.
![]() .
.
19.
![]() . 20.
. 20.
![]() .
.
21.
![]() . 22.
. 22.
![]() .
.
23.
![]() . 24.
. 24.
![]() . 25.
. 25.
![]() .
.
26.
![]() . 27.
. 27.
![]() . 28.
. 28.
![]() .
.
29.
![]() . 30.
. 30.
![]() .
.
Задача 4.
![]()
Задача 5. Найти частные производные функции двух переменных: а) частные производные первого порядка; б) производные от функции, заданной неявно; в) все частные производные второго порядка.





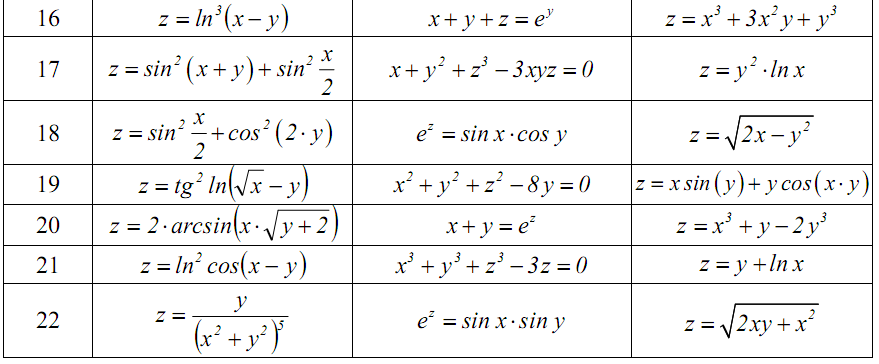
Задача 6. Выполнить только 1) и 3).


ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. 1.
Найти
![]() .
.
Решение. Так как под знаком предела стоит непрерывная в точке х=1 функция, то, используя определение непрерывной функции, имеем:
![]() .
.
Ответ.
![]() .
.
2. Найти
![]() .
.
Решение. Функция
![]() при
х=1 не определена («неопределенность
типа
при
х=1 не определена («неопределенность
типа
![]() »),
и, следовательно, не является непрерывной
в этой точке. Но при всех других значениях
х
»),
и, следовательно, не является непрерывной
в этой точке. Но при всех других значениях
х
![]() .
.
Полученная функция определена и непрерывна в точке х=1, поэтому
![]() =
=![]() =
=![]() .
.
Ответ:
![]() .
.
3. Найти
![]()
Решение. Здесь требуется найти
предел отношения двух бесконечно больших
величин. О таком пределе заранее ничего
определенного сказать нельзя
(«неопределенность типа
![]() »).
Преобразуем функцию под знаком предела,
вынося за скобки х в старшей степени,
и используем свойства бесконечно малых
и бесконечно больших величин. Тогда
имеем:
»).
Преобразуем функцию под знаком предела,
вынося за скобки х в старшей степени,
и используем свойства бесконечно малых
и бесконечно больших величин. Тогда
имеем:
![]()
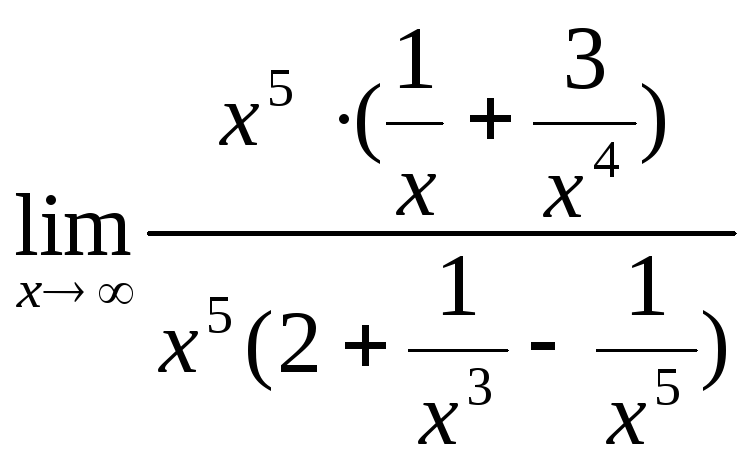 =
= =
=![]() =
=![]() =
0.
=
0.
Ответ: 0.
4. Найти
![]() .
.
Решение. Такого типа примеры решаются
переводом иррациональности из числителя
в знаменатель и, наоборот, из знаменателя
в числитель. Здесь мы имеем предел
разности двух положительных бесконечно
больших величин («неопределенность
типа [–]»).
От этой неопределенности избавимся,
дополнив функцию
![]() до разности квадратов:
до разности квадратов:
![]() =
=
![]() =
=
![]() =
=
![]() .
.
Следовательно,
![]() =
=
![]()
Ответ: 0.
5. Найти
![]() .
.
Решение. Так как
![]() (первый замечательный предел), то
(первый замечательный предел), то
![]() .
.
Следовательно,
![]() =
=![]()
Ответ:
![]() .
.
6. Найти
![]() .
.
Решение. Так как х→,
а не к 0, то применить сразу первый
замечательный предел нельзя. Поэтому
произведем замену переменной: –х
= у, откуда х = –у.
Тогда при х→
у→0, используя то, что
![]()
![]() =
=
![]() =
=
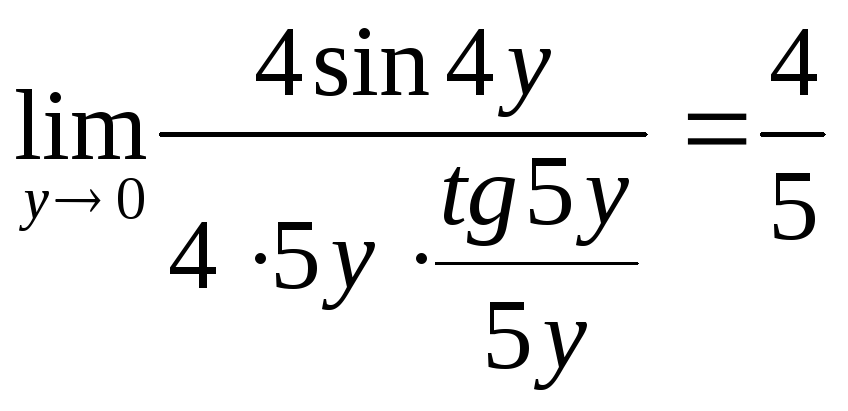 .
.
Ответ:
![]() .
.
7. Найти
![]() .
.
Решение. Выделим у дроби целую часть:
![]() .
.
Чтобы использовать второй замечательный
предел
![]() (или
(или
![]() ),
обозначим
),
обозначим
![]() .
Тогда при х→∞ у→0, причем
.
Тогда при х→∞ у→0, причем
![]() .
Т.о.
.
Т.о.
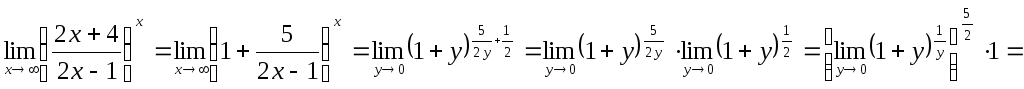 =
=![]() .
.
Ответ:
![]() .
.
Задача 2. Найдите производные функций:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() .
.
Решение. а) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:
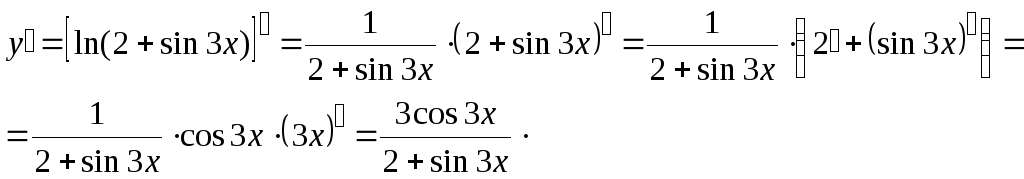
б)
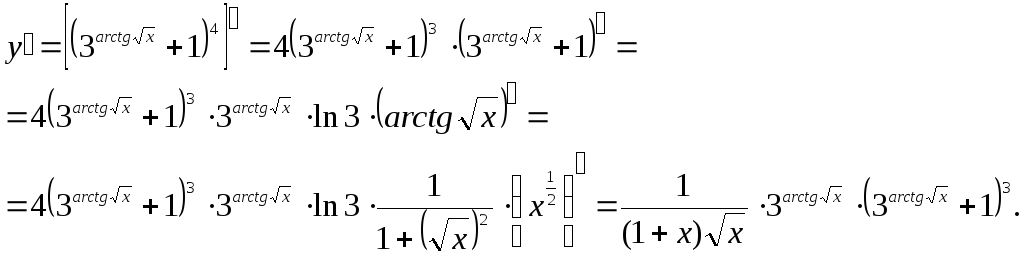
в) В данном случае
функциональная зависимость задана в
неявном виде. Для нахождения производной
![]() нужно продифференцировать по переменной
х
обе части уравнения, считая при этом у
функцией от х,
а затем полученное уравнение разрешить
относительно
нужно продифференцировать по переменной
х
обе части уравнения, считая при этом у
функцией от х,
а затем полученное уравнение разрешить
относительно
![]() :
:
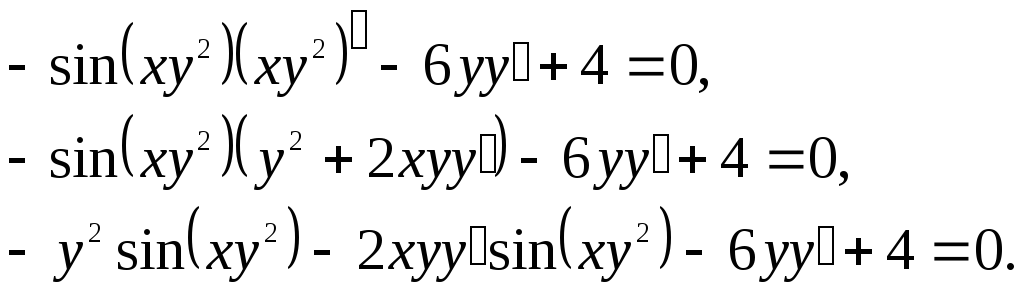
Из последнего
уравнения находим
![]() :
:
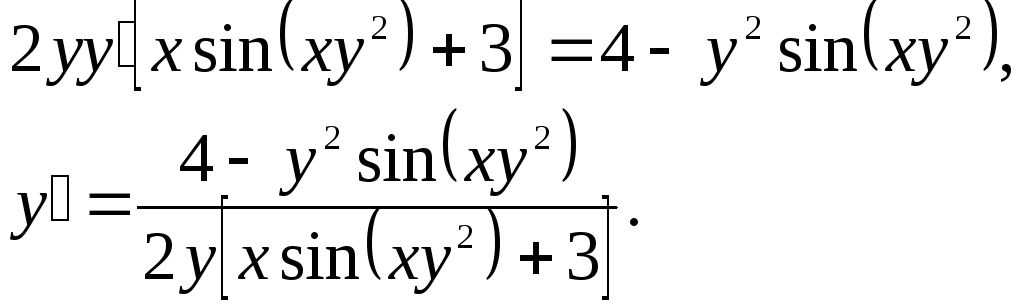
Задача
3. Исследовать
функцию
![]() и построить ее график.
и построить ее график.
Решение. Исследование функции проведем по следующей схеме:
-
Найдем область определения функции.
-
Исследуем функцию на непрерывность.
-
Установим, является ли функция четной, нечетной.
-
Найдем интервалы возрастания и убывания функции и точки экстремума.
-
Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.
-
Найдем асимптоты кривой.
Реализуем указанную схему:
-
Функция определена при всех значениях аргумента х, кроме
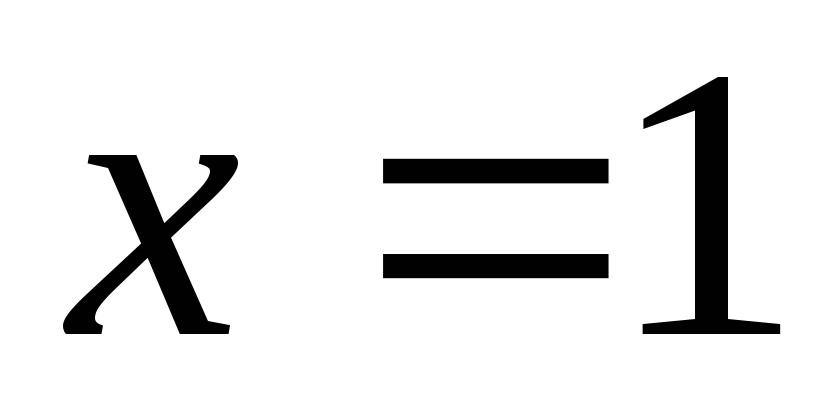 .
. -
Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах
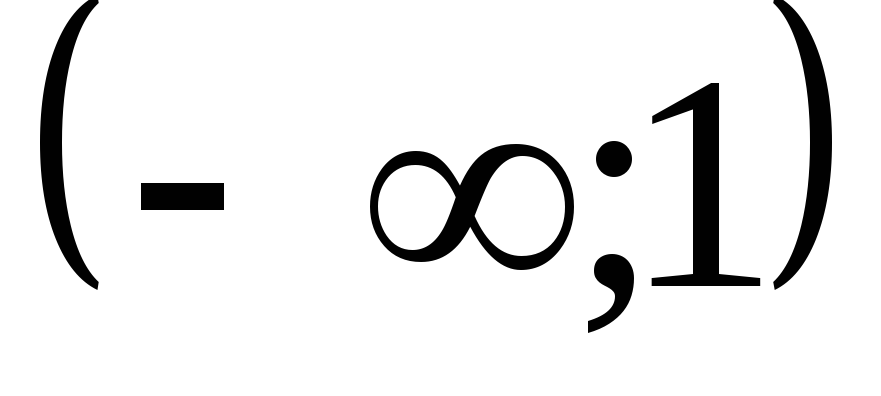 и
и
 .
В точке
.
В точке
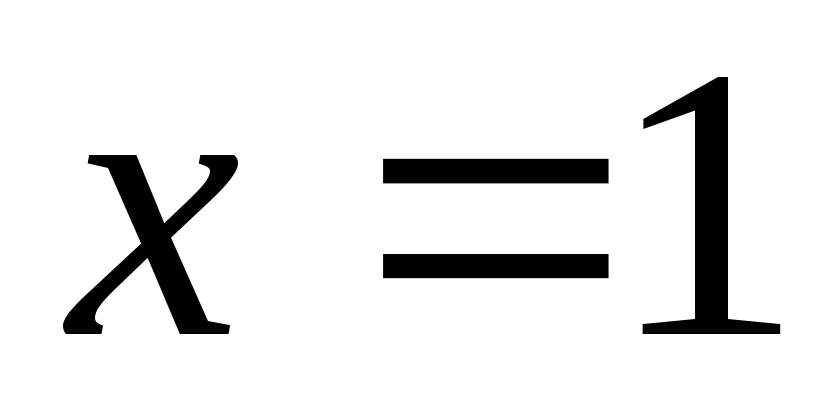 функция терпит разрыв второго рода.
функция терпит разрыв второго рода. -
Для установления четности или нечетности функции проверим выполнимость равенств
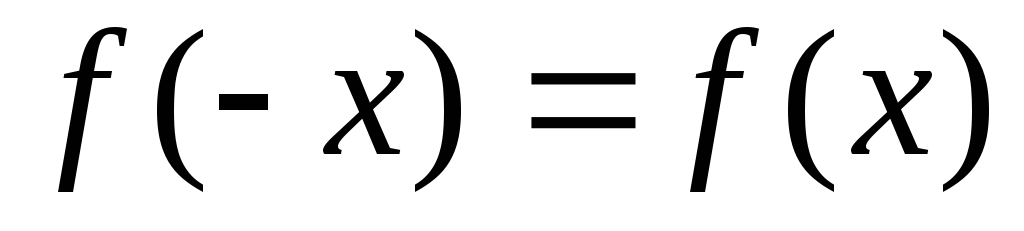 (тогда
(тогда
 – четная функция) или
– четная функция) или
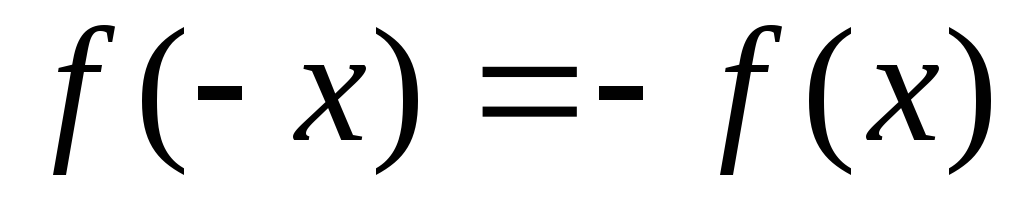 (для нечетной функции) для любых х
и –х
из области определения функции:
(для нечетной функции) для любых х
и –х
из области определения функции: