3.2.1. Критерий оптимальности по быстродействию

Важным и широко распространенным случаем поставленной выше оптимальной задачи является равенство единице подынтегральной функции (3.4):

(3.6)

В этом случае функционал (3.4) принимает значение:

и оптимальность управления U(t) означает минимальность времени перевода объекта управления из начального состояния в конечное положение . В этом случае задачу оптимального управления называют задачей об оптимальном быстродействии, а критерий оптимальности называется критерием оптимальности по быстродействию.

Применение данного критерия в технике и промышленности способствует повышению производительности работы машин, станков, технологического оборудования и т.д. Для конкретных технических задач критерий (3.4) с учетом (3.6) записывают в виде:

(3.7)

В первоначальном варианте принцип максимума был сформулирован на основе критерия оптимальности по быстродействию (3.10).

3.2.2. Функция управления

В принципе максимума функция управления U(t) для общего случая принята в виде кусочно-непрерывной функции (рис. 3.2).

Управление U(t) может иметь разрывы первого рода. На каждом отрезке времени функция управления , и т.д. является непрерывной во времени.

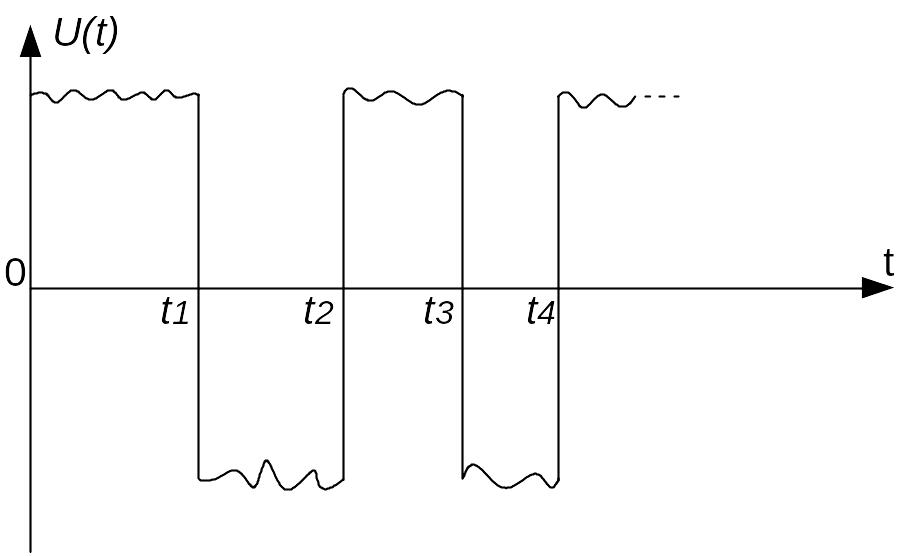
Рис. 3.2 Кусочно-непрерывное управление.

Однако из-за чрезвычайной сложности технической реализации на практике в основном применяется управление U(t) с кусочно-постоянной функцией U(t) (рис. 3.3).

Рис. 3.3 Кусочно-постоянное управление.

Моменты переключения управлений U(t): t₁, t₂, t₃,… являются параметрами синтеза оптимального управления и оптимального синтеза систем управления.

3.3 Геометрическое обоснование принципа максимума л.С. Понтрягина

Обоснование базируется на введении двух видов вариаций:

3.3.1. Игольчатая вариация

Пусть U(t) есть оптимальное управление. Мы имеем кусочно-непрерывные функции. Такая функция при больших вариациях может значительно осложнить задачу, т.к. мы можем оказаться в нелинейной области. В линейном плане такие вариации (имеется в виду вариации функционала) рассматривать уже нельзя. Выход из положения был найден. Основоположники принципа максимума предложили так называемую игольчатую вариацию, которая является эффектом от вариации управления U. При этой вариации функции U(t) рассматриваются в виде импульса малой длительности. В момент t₁ подается короткий импульс большой величины, например, 2U. Из-за инертности системы эффект от такого короткого импульса будет незначительным и потому задачу можно рассматривать в линейном плане.

После t₁ , т.е. после варьирования, траектория (рис. 3.4) пойдет выше. В конце получаем несколько отличный результат.

Рис. 3.4 Влияние игольчатой вариации на траекторию движения.

Если ввести n вариаций, то в результате получим n векторов смещения. Теперь, если натянуть оболочку на эти вектора, то получим выпуклый конус (рис. 3.5).

Рис. 3.5 Выпуклый конус.

В принципе максимума доказывается, что этот конус является выпуклым.

3.3.2. Временная вариация

Вторая часть доказательства связана с вариацией функции управления во времени  временной вариацией (рис. 3.6).

Рис. 3.6 Временная вариация.

Смысл этой вариации заключается в том, что в момент времени t₁ значение управления U оставляют постоянным в течении τ. Это означает, что система будет двигаться в фазовом пространстве по касательной (рис. 3.7).

Рис. 3.7. Эффект от временной вариации.

Время τ очень мало. Поэтому мы рассматриваем только первую производную и тем самым задача линеаризируется.

Если просуммировать эффект временных и игольчатых вариаций, то получим как бы раскрытую книгу. Она также является выпуклой (рис. 3.8).

Рис. 3.8 Эффект игольчатых и временных вариаций.

Имеем оптимальную траекторию, на которой построен конус в виде развернутой книги, которая является результатом временных и игольчатых вариаций.