3. Принцип максимума л. С. Понтрягина

3.1. Неклассическое вариационное исчисление

Классическое вариационное исчисление формировалось и развивалось в рамках аналитической динамики, электродинамики, термодинамики и других научных направлений физики в период с 18-го века и до первой половины 20-го века. Все вариационные методы и принципы были созданы для решения проблем физики и естественно не были ориентированы для решения вариационных задач современной техники.

Еще раз напомним основные положения классического вариационного исчисления. Вариации функционалов считались непрерывными и линейными. Переменные, входящие в функционал или в уравнения объекта управления, ограничений не имели.

Однако во многих практических задачах эти условия не соблюдаются. Известно, что управляющие воздействия, которые входят в функционалы, могут быть кусочно-непрерывными, т.е. претерпевать разрывы первого рода. Например, релейные элементы вырабатывают кусочно-непрерывные сигналы управления. Поэтому нарушаются условия непрерывности. Кроме того, на координаты и управления практически всегда накладываются ограничения.

Преодолеть эти условия с помощью классического вариационного исчисления более простыми способами не удается.

Во второй половине 20-го века были сформулированы вариационные принципы управления: принцип максимума Л. С. Понтрягина и принцип оптимальности Р. Беллмана. В них заложены фундаментальные положения математической теории оптимального управления. С этого времени начинает формироваться неклассическое вариационное исчисление [8, 11]. В рамках развития принципа максимума и принципа относительности в 90-х годах прошлого века был создан принцип конечно-временных вариаций оптимального быстродействия и метод варьирования свободных функционалов [2].

Вариационные принципы управления, как и вариационные принципы механики, играют важную роль в понимании процессов в природе и технике. Они имеют большую эвристическую ценность, обладают глубоким идейным смыслом, дают пути к единообразной трактовке различных физических процессов и общие подходы к их исследованию. Вариационные методы решения ряда теоретических и прикладных задач оказываются наиболее эффективными в качественном и, в ряде случаев, в количественном отношениях.

3.2. Постановка основной задачи принципа максимума

Принцип максимума позволяет находить оптимальное управление при наличии ограничений и выполнять оптимальный синтез систем управления. Изложение принципа максимума встречает большие трудности. Его доказательство базируется на функциональном анализе и теории множеств. Поэтому основные положения принципа приводятся способом геометрического толкования.

Рассмотрим объект управления в векторной форме:

(3.1)

или в скалярной форме:

(3.2)

и критерий оптимальности:

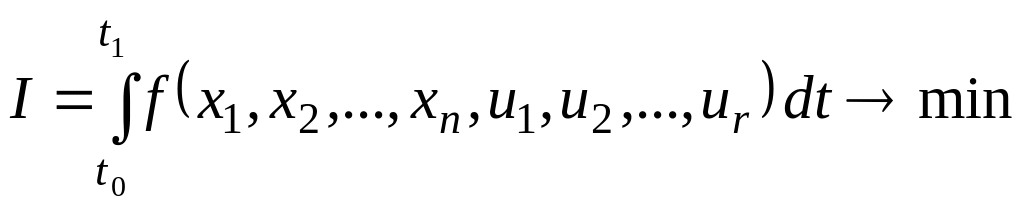(3.3)

Кроме того, заданы начальное состояние объекта и конечное положение .

Требуется так выбрать вектор управления , чтобы объект был переведен из в за минимальное время.

В начальном варианте принцип максимума был сформулирован как принцип оптимальности по быстродействию. В дальнейшем этот принцип получил более широкую трактовку, включая минимизацию расхода энергии на управление.

В выражениях (3.1÷3.3) обозначено:  вектор состояния объекта;  вектор управления;  координаты состояния объекта (например, угол поворота вала двигателя, скорость вращения вала и т.д.);  скалярные величины управления (управляющего воздействия); и  временные пределы интегрирования;  время перевода объекта из начального состояния в конечное положение.

В принципе максимума вводится новая координата [5, 11]

(3.4)

или

(3.5)

Соответственно движение системы (3.2) с учетом (3.5) рассматривается в (n+1)-мерном пространстве.

,

или в векторной форме

.

Причем в начальной точке при , , а в конечной точке при , .

Допустим, применено управление . Тогда будет решением уравнения при известных начальных условиях.

Представим это решение графически в трехмерном пространстве (рис. 3.1).

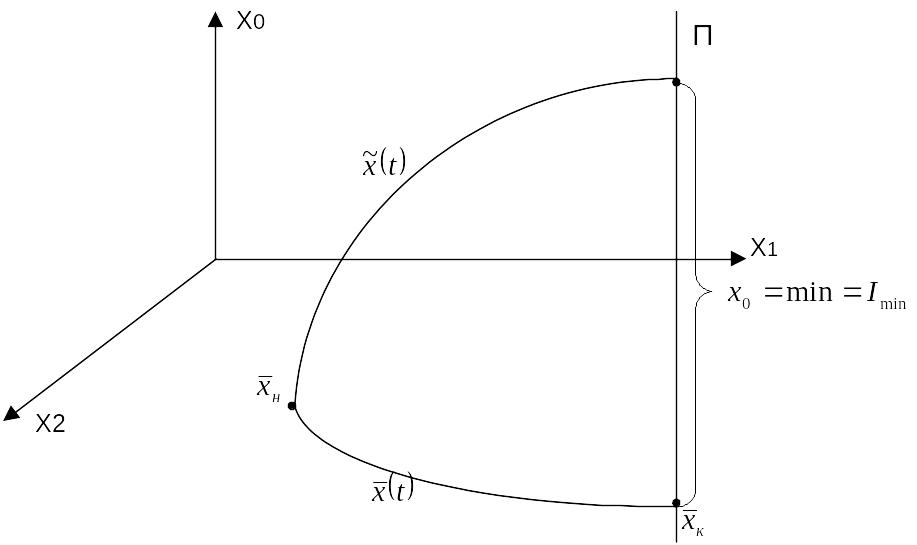
Рис.3.1 График движения траектории объекта с учетом x₀.

Через точку проводят прямую П, параллельную оси x₀. Тогда траектория  это траектория в плоскости x₁x₂, а является кривой функционала с учетом . То есть, мы рассматриваем движение объекта в плоскости, а с учетом в трехмерном пространстве.

Тогда основная задача отыскания оптимальных управлений может быть сформулирована следующим образом.

В фазовом пространстве X даны две точки и . Среди всех допустимых управлений U=U(t), переводящих объект из положения в положение , найти такое, для которого функционал (3.4) принимает наименьшее возможное значение.

Управление U(t), дающее решение поставленной задачи, называется оптимальным управлением, а соответствующая траектория х(t) – оптимальной траекторией.