4.Тригонометрическая форма записи комплексного числа.Формула Муавра.

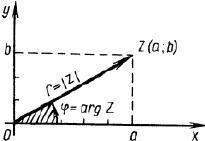
Для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

z = a + bi = r(cos φ + i sin φ)

Формула Муавра формула для нахождения n-й степени комплексного числа z, представленного в тригонометрической форме z = r(cosφ + isinφ);

5.Извлечение корня из комплексного числа.

Для любого ненулевого комплексного числа z=r(cosφ+isinφ) и любого n∈N существует только n комплексных чисел n-степень каждого из которых равна z. Этими числами является: β_s= 0≤S≤n-1

Согласно теореме об извлечении корня из комплексного числа (β₀)ⁿ=z

6. Понятие многочлена. Наибольший общий делитель.

Многочлен — это сумма одночленов.

Многочленом степени n(n=1.2…) от одного переменного над множеством действительных либо комплексных чисел называют любое отображение f заданного правилом: f:|R→|R (|R-множество действительных чисел).α в соответствии a₀ +a₁α+a₂α²…a_nαⁿ где a₀a₁..a_n-действительные числа, a_n≠0. F(α)= a₀ +a₁α+a₂α²…a_nαⁿ

Многочленом степени нуль называют отображение действующее по правилам: α в соответствии a₀(a₀≠0); f(x)= a₀≠0

Нулевым многочленом над множеством чисел называется отображение действий по правилу α в соответствии 0.

Многочлен степени нуль и нулевой многочлен называют постоянными многочленами на множеством действительных и комплексных чисел.

Для того чтобы 2многочлена P и Q были равны(как отображения) необходимо и достаточно чтобы коэффициенты при одинаковых степенях совпадали.

Многочлен R(x) называется общим делителем для многочленов P(x) и Q(x), если он служит делителем для каждого из этих многочленов.

Наибольшим общим делителем многочленов P(x) и Q(x) называется такой многочлен D(x), который является их общим делителем и вместе с тем сам делится на любой общий делитель этих многочленов.

7. Основная теорема. Следствие из основной теоремы.

Теорема: Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.

Следствие: Любой многочлен степени n над полем комплексных чисел имеет в нём ровно n корней, с учётом кратности корней.

Доказательство: У многочлена f(x) есть корень a, значит, по теореме Безу, он представим в виде (x-a)g(x) , где g(x) — другой многочлен. Применим теорему к g(x) и будем применять её таким же образом до тех пор, пока на месте g(x) не окажется линейный множитель.(Теорема Безу: При делении многочлена на (x-s) получается остаток, равный значению многочлена в точке s, то есть , где - многочлен степени n-1.

8. Понятие квадратичной формы. Приведение квадратичной формы к каноническому виду.

Квадратичной формой n переменных ,принимающих числовые значения , называется числовая функция вида где - числа, называемые коэффициентами квадратичной формы.

Матрица

называется матрицей квадратичной формы.

Рангом квадратичной формы называется ранг её матрицы.

Если матрица квадратичной формы L( ) невырожденная, то квадратичная форма-невырожденная.

Матрица наывается симметричной тогда, когда она совпадает с транспонированной матрицей.

Каноническая форма записи квадратичной формы, когда коэффициенты при произведении двух различных переменных равны 0.

Квадратичную форму называют положительно(отрицательно) определенной, если для всех переменных, среди которых хотя бы один элемент отличен от 0 выполняется L( )>0 (L( )<0)

Критерий Сильвестра: Для того, чтобы квадратичная форма была положительноопределенной необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительные.

У отрицательноопределенной квадратичной формы идет чередвание знаков с главным мнором(1ый минор со знаком минус) т.е. у «нечетных» главных миноров знак минус, а у «четных» -плюс.