
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:
где
Свойства определенного интеграла Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b].
Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то
Площадь криволинейной трапеции Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и графиком функцииf (x) (рисунок 1), определяется по формуле
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой
Замена переменной в определенном интеграле Определенный
интеграл
Новые пределы интегрирования по переменной t определяются выражениями
где g -1 - обратная функция к g, т.е. t = g -1(x). Интегрирование по частям для определенного интеграла В этом случае формула интегрирования по частям имеет вид:
где |
||||||
Пример 1 |
||||||
Вычислить
интеграл Решение. Применяя формулу Ньютона-Лейбница, получаем |
||||||
Пример 2 |
||||||
|
||||||
Вычислить
интеграл Решение. |
||||||
Пример 3 |
||||||
|
||||||
Вычислить
интеграл Решение. Сделаем замену: Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то t = 2. Тогда интеграл через новую переменную t легко вычисляется: |
||||||
Пример 4 |
||||||
|
||||||
Вычислить
интеграл Решение. Запишем интеграл в виде Используем
интегрирование по частям: Следовательно, интеграл равен |
||||||
Пример 5 |
||||||
|
||||||
Найти
площадь фигуры, ограниченной
кривыми Решение. Сначала определим точки пересечения двух кривых (рисунок 3). Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно, площадь фигуры равна
|
||||||
Пример 6 |
||||||
|
||||||
Найти
площадь фигуры, ограниченную графиками
функций Решение. Найдем координаты точек пересечения кривых (рисунок 4). Данная
область ограничивается сверху
параболой
,
а снизу - прямой линией |
||||||
Пример 7 |
||||||
|
||||||
Найти площадь треугольника с вершинами в точках (0,0), (2,6) и (7,1). Решение. Найдем сначала уравнение стороны ОА (рисунок 5). Аналогично, получим уравнение стороны ОВ. Наконец, найдем уравнение третьей стороны АВ. Как видно из рисунка 5, площадь треугольника равна сумме двух интегралов:
|
||||||
Пример 8 |
||||||
|
||||||
Вычислить
площадь эллипса Решение. В силу симметрии (см. рис.6), достаточно вычислить площадь полуэллипса, расположенного выше оси 0x, и затем результат умножить на 2. Площадь полуэллипса равна Для
вычисления данного интеграла используем
тригонометрическую подстановку x
= asin t,
dx = acos tdt.
Уточним пределы интегрирования.
Если x
= − a, то sin t =
−1 и Следовательно, полная площадь эллипса равна πab. |
Вычисление площади в декартовых координатах
Если
плоская фигура ограничена
прямыми x=a, x=b, a<b,
и кривыми ![]() ,
то ее площадь вычисляется по формуле
,
то ее площадь вычисляется по формуле
 (рис.
1).
(рис.
1).
Аналогично можно рассматривать фигуру относительно оси ОУ.
В
некоторых случаях границы х=а и х=b могут
вырождаться в точку пересечения
кривых ![]() .
.
В сложных случаях область следует разбить на фигуры, границы которых удовлетворяют указанным соотношениям.
При решении задач удобно придерживаться следующего порядка:
- построить в декартовых координатах фигуру, площадь которой требуется найти;
- найти точки пересечения кривых, образующих границу области для определения пределов интегрирования;
- записать формулу для вычисления и найти площадь.
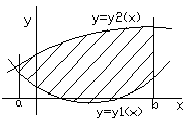
Рисунок 1.
Пример
1. Найти площадь фигуры, ограниченной
параболой ![]() и
прямой х+у=3.
и
прямой х+у=3.
Решение. Выполним построение и найдем точки пересечения параболы и прямой из системы уравнений
 .
.
Исключив ![]() из
системы, получим уравнение
из
системы, получим уравнение ![]() .
.
Корнями
этого уравнения являются ![]() и
и ![]() .
.

Рисунок 2.
Из
рисунка 2 видно, что ![]() на
отрезке [-2;1], поэтому формула для
вычисления площади имеет вид:
на
отрезке [-2;1], поэтому формула для
вычисления площади имеет вид:
 .
.
Пример
2. Вычислить площадь фигуры, лежащей в
первом квадранте, ограниченной кривыми ![]() .
.
Решение. Заданные уравнения определяют следующие кривые:
![]() -
парабола с вершиной в точке (0;0) и осью
симметрии ОХ;
-
парабола с вершиной в точке (0;0) и осью
симметрии ОХ;
![]() -
парабола с вершиной в точке (0;0) и осью
симметрии ОУ;
-
парабола с вершиной в точке (0;0) и осью
симметрии ОУ;
![]() -
окружность радиуса
-
окружность радиуса ![]() с
центром в точке (0;0). Фигура, образованная
кривыми, изображена на рисунке .3.
с
центром в точке (0;0). Фигура, образованная
кривыми, изображена на рисунке .3.

Рисунок 3.
Найдем координаты точек А, В, О.
Очевидно,
что О – начало координат. Точка А
образована пересечением кривых ![]() и
и ![]() .
Найдем ее координаты из решения системы
.
Найдем ее координаты из решения системы
 .
.
Исключая
у, получим уравнение: ![]() ,
корнями которого являются значения:
,
корнями которого являются значения: ![]() .
Поскольку фигура располагается в первом
квадранте, то следует оставить только
значение х=1, которому соответствует
ордината у=2, то есть точка А(1;2).
.
Поскольку фигура располагается в первом
квадранте, то следует оставить только
значение х=1, которому соответствует
ордината у=2, то есть точка А(1;2).
Найдем
координаты точки В, полученной пересечением
параболы ![]() и
окружности
и
окружности ![]() :
:
 .
.
При
решении системы удобно исключить х,
тогда из уравнения ![]() получим,
рассуждая по аналогии с предыдущим
случаем, координаты точки В(2;1).
получим,
рассуждая по аналогии с предыдущим
случаем, координаты точки В(2;1).
Если теперь обратиться к общей формуле вычисления площади
 ,
то можно заметить, что верхняя
кривая
,
то можно заметить, что верхняя
кривая ![]() задана
двумя разными уравнениями: на отрезке
[0;1] – это парабола
задана
двумя разными уравнениями: на отрезке
[0;1] – это парабола ![]() ,
а на отрезке [1;2] – дуга окружности
,
а на отрезке [1;2] – дуга окружности ![]() .
Нижняя кривая задана одним уравнением
.
Нижняя кривая задана одним уравнением ![]() на
всем отрезке [0;2]. Таким образом, при
вычислении площади основную фигуру
придется разбить на две и вычислить
площадь как сумму двух интегралов
на
всем отрезке [0;2]. Таким образом, при
вычислении площади основную фигуру
придется разбить на две и вычислить
площадь как сумму двух интегралов
 .
.
Вычислим каждый из интегралов отдельно.
 .
.

![]()
![]() .
.
Окончательно получаем
 .
.
Замечание
1. Интеграл  был
вычислен по частям:
был
вычислен по частям:

 ;
;
 ,
,
 .
.
Замечание 2. Поскольку искомая фигура симметрична относительно биссектрисы первого координатного угла, то вычисление интеграла можно было выполнять по переменной у совершенно аналогично:
 .
.
Вычисление площади в полярных координатах
Пусть
фигура представляет собой сектор,
заданный в полярной системе координат
кривой ![]() ,
где
,
где ![]() -
неотрицательная непрерывная кривая на
отрезке
-
неотрицательная непрерывная кривая на
отрезке ![]() .
Разобьем угол
.
Разобьем угол ![]() на n частей
лучами
на n частей
лучами![]() <
< ![]() <…<
<…< ![]() и
обозначим
и
обозначим ![]() (рисунок
4).
(рисунок
4).
П лощадь
криволинейного сектора равна
сумме n площадей
лощадь
криволинейного сектора равна
сумме n площадей ![]() ,
заданных разбиением
,
заданных разбиением ![]() , i =
1, 2, …, n,
, i =
1, 2, …, n,  .
.
Выберем
один из элементов разбиения ![]() ,
соответствующий сектору
,
соответствующий сектору ![]() ,
и зафиксируем на этом промежутке
произвольное значение
,
и зафиксируем на этом промежутке
произвольное значение ![]() .
Значение функции
.
Значение функции ![]() в
точке
в
точке ![]() обозначим
обозначим ![]() Рисунок
4
Рисунок
4
и
заменим площадь криволинейного сектора
круговым сектором радиуса ![]() ,
площадь которого
,
площадь которого ![]() .
Выполним такую же операцию на каждом
участке разбиения
и
просуммируем полученные значения.
.
Выполним такую же операцию на каждом
участке разбиения
и
просуммируем полученные значения.
Сумма площадей круговых секторов

представляет
собой интегральную сумму , предел
которой, существующий в силу непрерывности
функции ![]() ,
равен определенному интегралу, выражающему
площадь фигуры в полярных координатах
,
равен определенному интегралу, выражающему
площадь фигуры в полярных координатах

При вычислении площади фигуры в полярных координатах рекомендуется придерживаться такого же порядка исследования, что и в декартовых координатах: построение чертежа, вычисление точек пересечения кривых, образующих границу фигуры; запись формулы.
Пример
1. Найти площадь фигуры, ограниченной
кардиоидой ![]() и
окружностью
и
окружностью ![]() .
.
Решение. Выполним построение фигуры (рисунок 5).

Рисунок 5.
Из рисунка видно, что пересечение кривых образует три различных фигуры: вне круга, вне кардиоиды и внутренняя часть кардиоиды и окружности. Рассмотрим вычисление площади одной из них, расположенной вне кардиоиды (заштрихованная часть на рисунке).
Найдем точки пересечения кривых из системы
 ,откуда
,откуда ![]()
 ;
;
 .
.
При  искомая
площадь представляет собой часть круга,
вырезанного кардиоидой, поэтому следует
рассмотреть разность площадей
искомая
площадь представляет собой часть круга,
вырезанного кардиоидой, поэтому следует
рассмотреть разность площадей ![]() ,
где
,
где ![]() -
площадь полукруга, а
-
площадь полукруга, а ![]() -
площадь, ограниченная кардиоидой и
лучами
-
площадь, ограниченная кардиоидой и
лучами ![]() .
.
Согласно
формуле  запишем
запишем


![]() .
.
Замечание.
Для вычисления площади, образованной
пересечением заданных кривых, расположенной
вне круга, надо рассмотреть разность
площадей, ограниченных кардиоидой и
кругом при ![]() .
.
Для
вычисления внутренней части кардиоиды
и окружности надо рассмотреть сумму
площадей, одна из которых представляет
половину круга при
,
а вторая – сегмент кардиоиды при ![]() .
.
Пример 2. Найти площадь фигуры, ограниченной кривой
![]() >0.
>0.
Решение.
Перейдем к полярным координатам
и,используя формулы ![]() ,
запишем уравнение кривой :
,
запишем уравнение кривой :
![]() ,
,
![]() ,
,
![]() .
.
Так
как ![]() ,
то уравнение примет вид
,
то уравнение примет вид
![]() ,
,
 ,
,
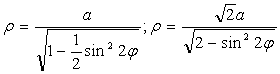 .
.
Из
формулы следует, что ![]() определено
для
определено
для ![]() ,
, ![]() для
любого значения
для
любого значения ![]() ,
принимает наибольшее значение
,
принимает наибольшее значение ![]() при
при ![]() , n –
целое, и наименьшее значение
, n –
целое, и наименьшее значение ![]() при
при ![]() (рисунок
6).
(рисунок
6).

Рисунок 6.
Площадь
ограничена замкнутой кривой, симметричной
относительно полярной оси и лучей ![]() ,
потому достаточно вычислить одну восьмую
часть площади и умножить полученный
результат на восемь:
,
потому достаточно вычислить одну восьмую
часть площади и умножить полученный
результат на восемь:

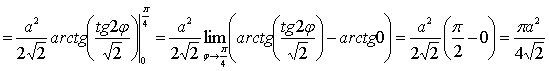 ;
;
 .
.



 где k -
константа;
где k -
константа;




 по
переменной x можно
преобразовать в определенный интеграл
относительно переменной t с
помощью подстановки x
= g (t):
по
переменной x можно
преобразовать в определенный интеграл
относительно переменной t с
помощью подстановки x
= g (t): .
.
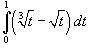 .
.
 .
.
 .
.







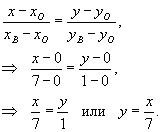
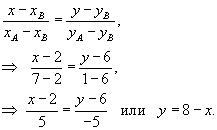



 .
.
