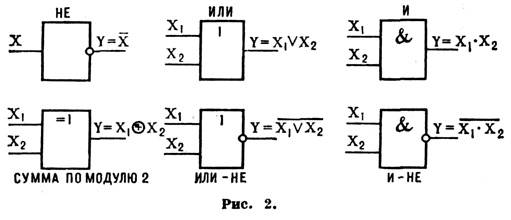
2. Булевы функции: эквивалентность и сумма по модулю два. Таблицы истинности, комбинационные схемы, изображение базисных элементов.
Сложе́ние по мо́дулю 2 (логи́ческое сложе́ние, исключа́ющее «и́ли», строгая дизъюнкция, XOR) — булева функция и логическая операция. Результат выполнения операции является истинным, если только один из аргументов является истинным. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Сложение по модулю 2 следует отличать от простого сложения, которое соответствует обыкновенному неисключающему «или» (логической дизъюнкции).
В теории множеств сложению по модулю 2 соответствует операция симметричной разности двух множеств.
Чаще всего встречаются следующие варианты записи:
^
a
≠ b,
Таблицы истинности:
Правило (только
для бинарного сложения по модулю 2):
результат равен
,
если оба операнда равны; во всех остальных
случаях результат равен
.
Эквивалентность
. Эквивалентностью (или эквиваленцией)
двух высказываний x
1
и x
2
называется новое высказывание, которое
считается истинным, когда оба высказывания
x 1
и x
2
либо одновременно истинны, либо
одновременно ложны, и ложным - во всех
остальных случаях.
Эквивалентность
высказываний x
1
и x
2
обозначается символом x
1 
x 2
(или x 1 =
x 2,
или x 1
x
2),
читается " для
того, чтобы x
1,
необходимо и достаточно, чтобы x
2"
или " x 1
тогда и только
тогда, когда x
2".
Высказывания x
1
и x 2
называются членами эквивалентности.
Логические
значения операции эквивалентности
описываются следующей таблицей
истинности.
x 1 |
x 2 |
x 1 x 2 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
3. Булевы функции: Штрих шеффера и стрелка Пирса.
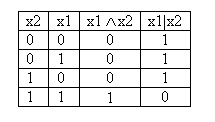
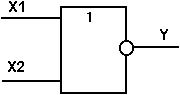
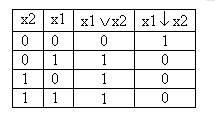
Определение: Штрихом Шеффера называется функция двух переменных, которая обозначается x1|x2, читается «отрицание конъюнкции» и считается ложной тогда и только тогда, когда оба аргумента истинны.
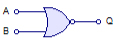
Определение: Стрелкой Пирса называется функция двух переменных, которая обозначается x1 \|/ x2, читается «отрицание дизъюнкции» и считается истинной тогда и только тогда, когда оба аргумента ложны.
=================================================================================
4. Совднф и совкнф. 5. 6. Построение их по таблице истинности
Совершеная дизъюнктивная нормальная форма (СДНФ)> – такая дизъюнкция конъюнкций, в которой:
Различны все члены конъюнкции ("множители");
Различны все члены каждой дизъюнкции ("слагаемые");
В каждой дизъюнкции нет одновременно переменной и ее отрицания;
Каждая дизъюнкция содержит все переменные, входящие в данную формулу или их отрицания.
СДНФ:
Приведение формулы к СДНФ с помощью равносильных преобразований:
Привести формулу к нормальному виду (т.е. избавиться от импликации, эквиваленции и отрицания неэлементарных формул).
Из всех одинаковых членов дизъюнкции ("слагаемых") оставить только один.
Если в каком-то члене дизъюнкции ("слагаемом") не хватает переменной Xi, то "домножаем" его с на (Xi?¬Xi), т.е. на 1 .
Раскрыть скобки и из всех одинаковых членов дизъюнкции ("слагаемых") оставить только один.
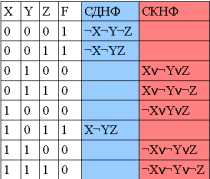
Для построения СДНФ по таблице истинности необходимо:>
Выбрать из таблицы истинности те строки, в которых значение формулы - "Истина".
Для каждой выбранной строки составить конъюнкцию переменных или их отрицаний так, чтобы эта конъюнкция была истинной (для этого переменные, которые в соответствующей строке имеют значение "Ложь" нужно взять с отрицанием, а переменные, имеющие значение "Истина" - без отрицания).
Составить дизъюнкцию полученных конъюнкций.
Совершеная конъюнктивная нормальная форма (СКНФ) – такая конъюнкция дизъюнкций, в которой:
Различны все члены дизъюнкции ("слагаемые");
Различны все члены каждой конъюнкции ("множители");
В каждой конъюнкции нет одновременно переменной и ее отрицания;
Каждая конъюнкция содержит все переменные, входящие в данную формулу или их отрицания.
Приведение формулы к СКНФ с помощью равносильных преобразований:
Привести формулу к нормальному виду (т.е. избавиться от импликации, эквиваленции и отрицания неэлементарных формул).
Из всех одинаковых членов конъюнкции ("множителей") оставить только один.
Если в каком-то члене конъюнкции ("множителе") не хватает переменной Xi, то "прибавить" к нему (Xi?¬Xi), т.е. 0 .
Раскрыть скобки и из всех одинаковых членов конъюнкции ("множителей") оставить только один.
Построение СКНФ потаблице истинности:
Выбрать из таблицы истинности те строки, в которых значение формулы - "Ложь".
Для каждой выбранной строки составить дизъюнкцию переменных или их отрицаний так, чтобы эта дизъюнкция была ложной (для этого переменные, которые в соответствующей строке имеют значение "Истина" нужно взять с отрицанием, а переменные, имеющие значение "Ложь" - без отрицания).
Составить конъюнкцию полученных дизъюнкций.
==================================================================================