50. Строки символов как примеры полугрупп и моноидов - ????????????????.
51. Понятие группы.
Гру́ппа — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам.
Группы являются важными инструментами в изучении симметрии во всех её проявлениях. Ветвь математики, занимающаяся группами, называется теорией групп.
Примерами групп являются вещественные числа с операцией сложения, множество вращений плоскости вокруг начала координат и т. п.
Непустое множество
с
заданной на нём бинарной
операцией
называется
группой
,
если выполнены следующие аксиомы:
ассоциативность:
;
наличие нейтрального
элемента:
;
наличие обратного
элемента:
52. Подгруппы. Построение подгрупп заданной группы.-???????????????????
Определение 3.42.
Подмножество
основного
множества
группы
G =
называется
подгруппой группы G, если оно само
является группой относительно бинарной
операции
.
Теорема 3.7 (критерий
подгруппы). Пусть G =
–
группа и
H
=
–
подгруппа группы G, если выполняются
следующие условия:
1) для любых элементов
элемент
также
принадлежит множеству
2) для каждого
элемента
симметричный
ему элемент
также
принадлежит множеству
Замечания.
1. Любая группа является своей подгруппой.
2. Множество, состоящее только из нейтрального элемента группы, также будет подгруппой этой группы.
3. Требование для подгруппы быть группой относительно той же бинарной операции, которая определена в основной группе, является существенным и его нельзя нарушать.
Примеры.
1. Рассмотрим
группу T =
всех
отображений
относительно
операции
композиции
отображений. Нейтральным элементом
этой группы относительно операции
является
отображение
,
а симметричным для элемента
является
отображение
.
Очевидно, что множество
является
подмножеством основного множества этой
группы. Покажем, что
–
подгруппа группы T. Для этого воспользуемся
критерием подгруппы, сформулированным
в теореме 3.7:
1) пусть
произвольные
элементы множества
,
тогда композиция
также
является элементом множества
;
2) для
любого элемента
множества
симметричный
ему элемент
также
принадлежит множеству
.
2. Аддитивная группа чётных чисел 2Z является подгруппой аддитивной группы целых чисел Z, которая, в свою очередь, является подгруппой аддитивной группы рациональных чисел.
Везде далее, не
уменьшая общности, будем рассматривать
мультипликативную запись группы G =
В
этом случае симметричным элементом для
элемента
будет
обратный элемент
Пусть H =
подгруппа
группы G. Зададим на множестве
бинарное
отношение
следующим
образом:
для
любых
.
Определение 3.43. Бинарное отношение , заданное на множестве , называется отношением сравнения группы G по подгруппе H.
Теорема 3.8. Пусть H = – подгруппа группы G = . Отношение сравнения группы G по подгруппе H является отношением эквивалентности.
Определение 3.44. Класс эквивалентности отношения сравнения группы G по подгруппе H называется левым смежным классом группы G по подгруппе H:
Рассмотрим свойства левых смежных классов группы по подгруппе, сформулированные в следующих теоремах.
Теорема 3.9. Любые два левых смежных класса группы G по подгруппе H либо совпадают, либо не пересекаются.
Теорема 3.10 (о
структуре левого смежного класса). Если
некоторый
элемент группы G, то множество
является левым
смежным классом группы G по подгруппе
H, порождённым элементом
Теорема 3.11. Пусть
левые
смежные классы группы G по подгруппе H,
порождённые элементами
соответственно.
Множества
и
совпадают
тогда и только тогда, когда порождающие
их элементы находятся друг с другом в
отношении сравнения группы G по подгруппе
H:
Аналогично
можно ввести понятие правого смежного
класса группы G по подгруппе H. Для этого
достаточно задать на множестве
бинарное
отношение
для
любых
.
Это отношение
также является отношением эквивалентности.
Классы эквивалентности по бинарному
отношению
будут
называться правыми смежными классами
группы G по подгруппе H. Для правых смежных
классов группы по подгруппе справедливы
свойства, аналогичные тем, которыми
обладают левые смежные классы. По
структуре правый смежный класс группы
G по подгруппе H, порождённый элементом
представляет
собой множество
Теорема 3.12. Пусть H – подгруппа группы G. Отображение
множества левых смежных классов группы G по подгруппе H на множество правых смежных классов является биективным.
Следствие 3.1. Число правых и левых смежных классов группы G по подгруппе H совпадает.
Примеры.
1. Найдём смежные
классы мультипликативной группы отличных
от нуля комплексных чисел С =
по
подгруппе положительных действительных
чисел R+ =
Для
этого рассмотрим два произвольных
элемента множества
:
.
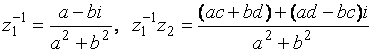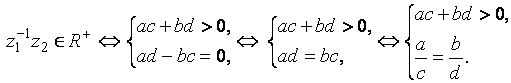
Следовательно, в один и тот же левый смежный класс группы С по подгруппе R+ войдут такие отличные от нуля комплексные числа, отношения действительных частей которых равно отношению мнимых частей, а сумма произведений действительных частей и мнимых частей положительна. Аналогично описываются правые смежные классы группы С по подгруппе R+.
2. Рассмотрим
подгруппу S =
группы
подстановок третьей степени S3 =
.
Найдём правые и левые смежные классы
группы S3 по подгруппе S. При этом
воспользуемся таблицей Кэли (см. табл.
3.2), полученной для группы S3:
1)
первый
правый смежный класс;
2)
второй
правый смежный класс;
3)
второй
правый смежный класс;
4)
первый
правый смежный класс;
5)
первый
левый смежный класс;
6)
первый
левый смежный класс;
7)
второй
левый смежный класс;
8)
второй
левый смежный класс.