Министерство науки, высшей школы и технической политики

Российской Федерации

Ивановский ордена Трудового Красного Знвмени

химико-технологический институт

211

МОДЕЛИРОВАНИЕ СЛОЖНЫХ ИЗОТЕРМИЧЕСКИХ РЕАКЦИЙ,

ОПИСЫВАЕМЫХ. ЛИНЕЙНЫМИ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ

Методические указания

Составители: В.А.Таланова

C. М. Чаусова

Иваново 2008

КУРСОВАЯ РАБОТА ПО ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКЕ И

ПРОГРАММИРОВАНИЮ

Наименование: Моделирование сложных изотермических реакций, опи­сываемых линейными дифференциальными уравнениями .

1.1 Содержание работы и порядок выполнения

Задача, предлагаемая в курсовой работе - задача прямого моде­лирования - получение однозначного решения при условии, что матема­тическая модель определена полностью, т.е. известны все параметры модели, начальные условия, задается:

Схема механизма химической реакции.

Константы скоростей отдельных стадий реакции.

Начальные концентрации компонентов.

Продолжительность реакции.

Метод численного решения дифференциальных уравнений кинетики.

Требуется:

1.Составить кинетическую модель данной химической реакции.

2. Выполнить на калькуляторе численное решение дифференциальных

уравнений кинетики с целью получения кинетических зависимостей компонентов реакции в виде таблиц и графиков функций (t) для пяти равноотстоящих значений t .

2. Выполнить программирование задачи для ЦВМ на алгоритмическом

Языке Паскаль.

3. Решить задачу на ПК для 20 равноотстоящих значений t .

1.2. Содержание и оформление отчета

Отчет по курсовой работе должен включать формулировку задания, а также подробное описание порядка выполнения работы в соот­ветствии с предыдущим разделом ''Содержание и порядок выполнения".

В отчете должны быть представлены:

система дифференциальных уравнений, представляющая кинетичес­кую модель данной химической реакции;

описание метода численного решения системы дифференциальных уравнений;

результата численного решения задачи на калькуляторе в виде таб­лиц, графиков»

Паскаль-программа решения задачи или решение с помощью Excel;

результаты решения задачи на ПК в виде таблиц и графиков реше­ний, построенных на миллиметровой бумаге. Отчет оформляется в тонкой (12 листов) ученической тетради.

2. ПОСТАНОВКА ЗАДАЧИ

Маршрут химической реакции принято отражать с помощью стехио-метрического уравнения, которое показывает, в каких соотнешениях вещества вступают во взаимодействие.

Компоненты реакции обозначают буквами А,В,С,...

Например, А + В ->2С - стехиометрическое уравнение.

Если стехиометрическое уравнение отражает механизм химичес­кой реакции, то оно служит основанием для составления кинетичес­ких уравнений.

Кинетические уравнения определяют связь между скоростью хи­мической реакции и концентрациями реагирующих веществ.

Кинетические уравнения записываются на основании закона действующих масс, в соответствии с которым, скорость химической реакции пропорциональна концентрациям взаимодействующих веществ и не зависит от концентрации продуктов.

Так, для приведенного выше стехиометрического уравнения имеем:

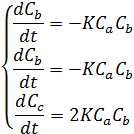
здесь к - константа скорости химической реакции.

Решая систему дифференциальных уравнений с некоторыми задан­ными начальными условиями получим кривые зависимости , , - кинетические кривые, таким образом, можем рассчитать концентрации компонентов в определенный момент временя.

3. НЕКОТОРЫЕ МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Математическое моделирование кинетики сложных химических реак­ций сводится к решению систем обыкновенных дифференциальных урав­нений вида

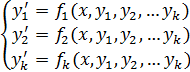
с начальными условиями , где i=I,…,K .

Как правило, система уравнений, описывающих кинетику изучаемой реак­ции является нелинейной и поэтому не может быть решена аналитически. Возникает необходимость использования методов приближенного числен­ного интегрирования.

Эти методы позволяют приближенно отыскать решение дифференциа­льных уравнения только на некотором конечном интервале [а,b].

Пусть, имеем, некоторое дифференциальное уравнение первого порядка y=f(x,y) с начальными условиями . Будем искать решение этого уравнения на отрезке [ ]. Разобьем этот отрезок на n равных частей. Тогда получим систему равноотстоящих узлов

Здесь - шаг интегрирования.

Численные методы дают возможность найти в некотором числе точек приближения для значений точного решения

.

Наиболее простым методом решения дифференциальных уравнений и их систем является

3.1. Метод Эйлера

Пусть дано дифференциальное уравнение (I), с на­чальными условиями y(

Пусть y=y(x) искомое точное решение. Интегральная кривая проходит через точку (

Найдем приближенные значения функции в точках . Построим систему равноотстоящих точек узлов

Проведем прямые

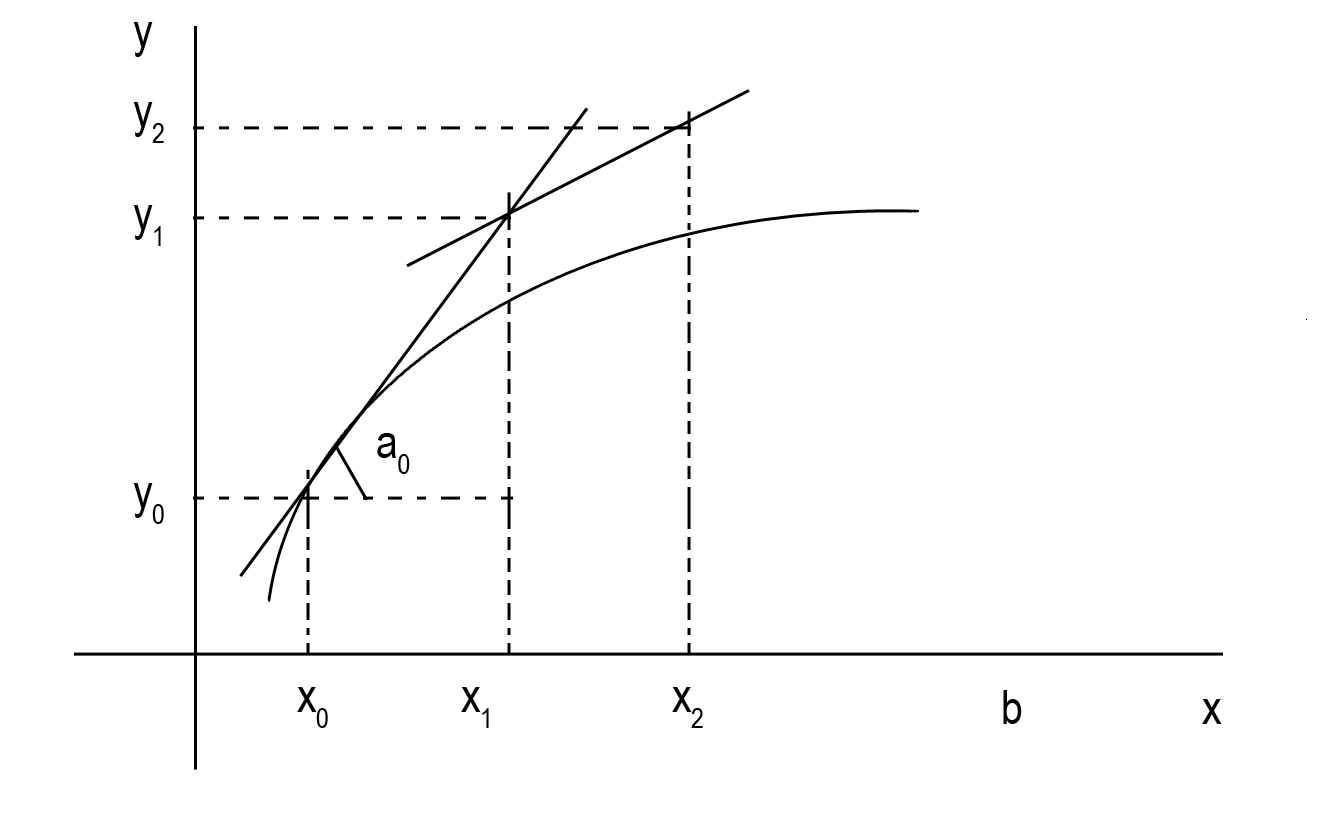
Рассмотрим отрезок [ ]

На этом отрезке есть одна точка, которая принадлежат искомой кри­вой - это точка А Заме­ним дугу искомой кривой y=y(x) на отрезке [ ] касательной к ней, проведенной в точке ( )

В качестве возьмем ординату точки пересечения прямой x= с касательной.

Очевидно . Но ,

т.е. .

Но из уравнения (I) следует, чтo

Итак, получаем .

Предположим теперь, что точка принадлежит искомой кривой. В этой точке опять проведем касательную к графику функции до пересечения с прямой х = .

Тогда аналогично:

.

Продолжая и так далее, получим систему значений которые и будут приближенными значениями функции y=y(x) в точках

Итак, расчетные формулы метода Зилера:

.

Для системы дифференциальных уравнений

i= I,…,k

расчетные формулы записываются аналогично

здесь i - номер уравнения в системе, n - номер шага.

Метод Эйлера является грубым методом, ошибка, которую мы допус каем ка каждом шаге пропорциональна , т.е. .

Чтобы повысить точность вычислений, использует некоторые усовершенствованные методы.

3.2. Метод Эйлера-Коши

Пусть опять решаем уравнение y’=f(x,y), y(

Решение ищем на отрезке [ ].

П усть нам известны координаты некоторой точки, принадлежащей ис­комому решению ( ). Найдем средний тангенс угла наклона ка­сательной для двух точек : ( ) и ( ).

Последняя точка, есть та самая, которую в методе Эйлера мы обоз­начаем ( ), но здесь точка будет вспомогательной.

Итак, сначала по методу Эйлера находится точка А, лежащая на прямой , тангенс угла накло­на которой

В этой точке снова вычисляется тангенс угла наклона касательной

Затем через точку ( ) проводим прямую L, тангенс уг­ла наклона которой равен

Точка, в которой L пересе­чется с прямой ,будет искомой( ). Таким обра­зом, есть искомое приближение значения функции на данном шаге интегрирования.

Расчетные формулы метода Эйлера-Коша следующие:

Аналогично, для системы дифференциальных уравнений:

Здесь i - номер уравнения системы, m - номер шага.

Пример.

Задано:

Уравнение уу + 2х² = 0 на интервале [1,2] при условии у(1) = 3. Представим уравнение в виде у = -2х²/у. Разобьем интервал [1,2] на десять шагов с шагом h = 0,1.

Расчетные формулы метода Эйлера-Коши:

Первый шаг (i = 0):

х₁ = х₀ + h = 1 + 0,1 = 1,1;

₁= y₀ + h  f(y₀, x₀) = 3 + 0,1(-21²)/3 = 2,93.

х₂ = х₁ + h = 1,1 + 0,1 = 1,2;

y₂ = y₁ + (h/2)  (f(y₀, x0)+ f( ₁, x₁)) = 2,93 + (0,1/2)*((-21,1²)/2,93+(- 2*1,1^2/2.93)) = 2,85633.

Аналогично можно найти значения искомой величины на всём интервале.

Полученные данные позволяют построить график искомой функции на заданном интервале изменения аргумента: