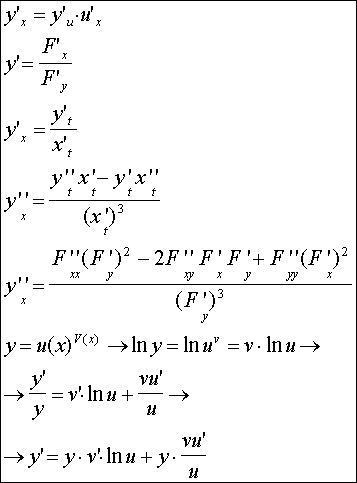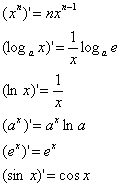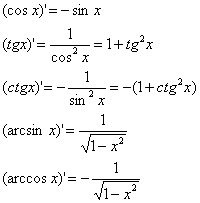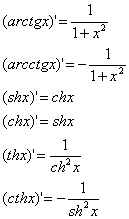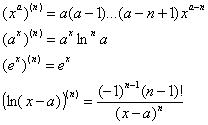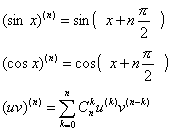- •В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме, проекция вектора на ось
- •В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме
- •В.13 Векторное произведение
- •В.14 Смешанное произведение
- •Плоскость в пространстве
- •Прямая и плоскость в пространстве
- •. Поверхности второго порядка
- •Предел функции в точке и на бесконечности
- •II способ. Чтобы избавится от неопределенности вида , введем замену переменной , т.К. При получим .
- •. Односторонние пределы: Асимптоты графика функции.
- •Дифференцирование функции с переменной в основании степени и в показателе
- •Дифференцирование функций, заданных неявно и параметрически.
Дифференцирование функции с переменной в основании степени и в показателе
Пример 1. Найти производную функции с помощью логарифмического дифференцирования:
Решение.
1. Функция
![]() является показательно-степенной.
Прологарифмируем её по основанию e:
является показательно-степенной.
Прологарифмируем её по основанию e:
![]()
![]() .
.
Дифференцируем обе части полученного равенства, учитывая, что y – это функция от x. Используя формулы дифференцирования сложной функции и произведения функций, получаем:
![]()
![]()
![]()
Выразим
![]() из последнего равенства:
из последнего равенства:
![]() .
.
Подставим вместо
переменной
![]() заданное выражение и приходим к ответу
заданное выражение и приходим к ответу
![]()
2.
![]() .Прологарифмируем
равенство, задающее функцию по основанию
.Прологарифмируем
равенство, задающее функцию по основанию
![]() и используем основные свойства логарифмов:
и используем основные свойства логарифмов:
![]() ;
;
![]() ;
;
![]()
Дифференцируем полученное равенство при условии, что y – это функция от x.
![]()
Выразим далее
![]() и заменим переменную y
заданным
выражением:
и заменим переменную y
заданным
выражением:
![]() ;
;
 .
.
Пример 2. Вычислить производную показательно-степенной функции, используя переход к основанию e:
![]()
Решение: Используем формулу (3).
![]()
Полученную функцию продифференцируем по правилу вычисления производной сложной функции:
![]()
![]()
![]()
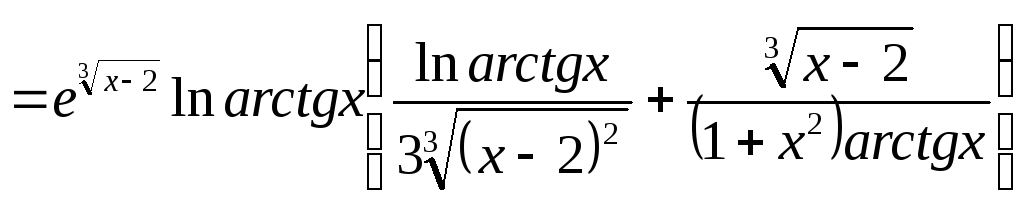 .
.
Дифференцирование функций, заданных неявно и параметрически.
Пример 1: Найти
производную
![]() функции, используя возможные способы
функции, используя возможные способы
1)
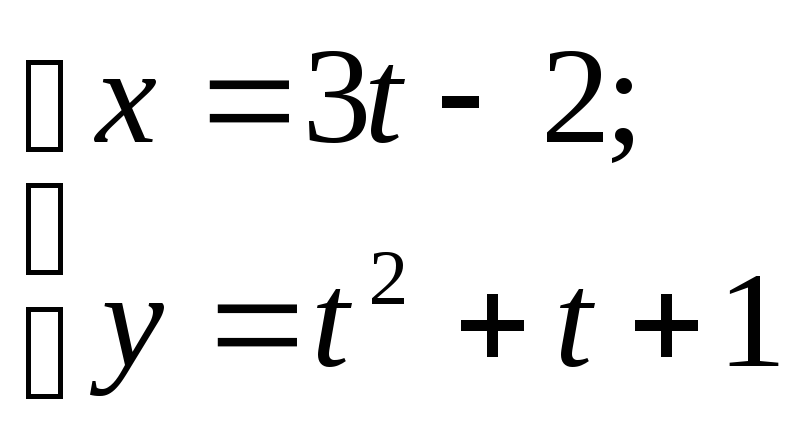 2)
2)
![]()
Решение.
1) I
способ. Из
первого уравнения системы выразим
![]() через
через
![]() :
:
![]() .
.
Полученное выражение
подставим во второе уравнение вместо
![]() :
:
![]() .
.
Получили функцию
одной переменной
![]() .
Дифференцируем её:
.
Дифференцируем её:
![]() .
.
II способ. Используем формулу (6):
![]() .
.
В полученное
выражение подставим
![]() ,
получим:
,
получим:
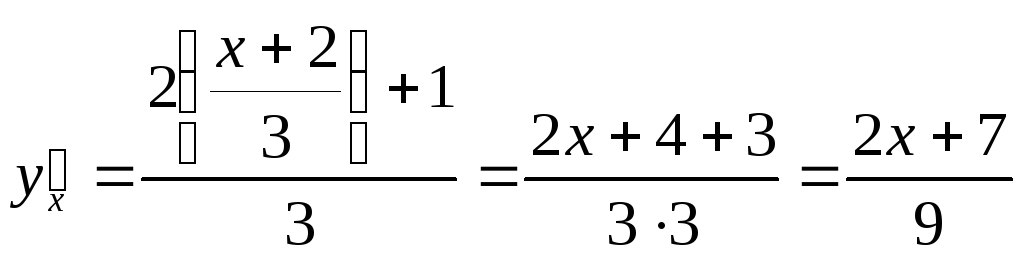 .
.
I способ.
2. Выразим из первого
уравнения системы переменную
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Подставляем во
второе уравнение системы, получим
сложную функцию переменной
![]() :
:
![]() ,
которую продифференцируем по правилу
вычисления производной сложной функции:
,
которую продифференцируем по правилу
вычисления производной сложной функции:
![]()
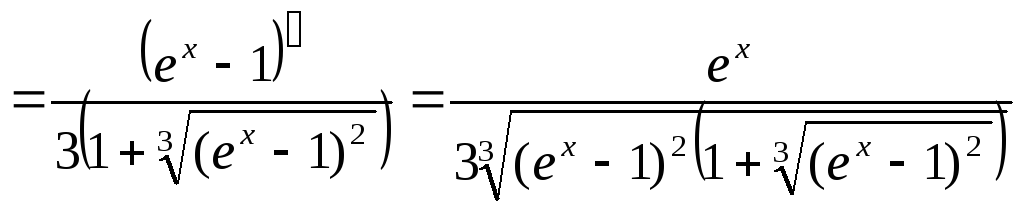 .
.
II способ. Воспользуемся формулой (6):
![]() ;
;
![]() .
.
Подставляя выраженія в формулу (6), получим:
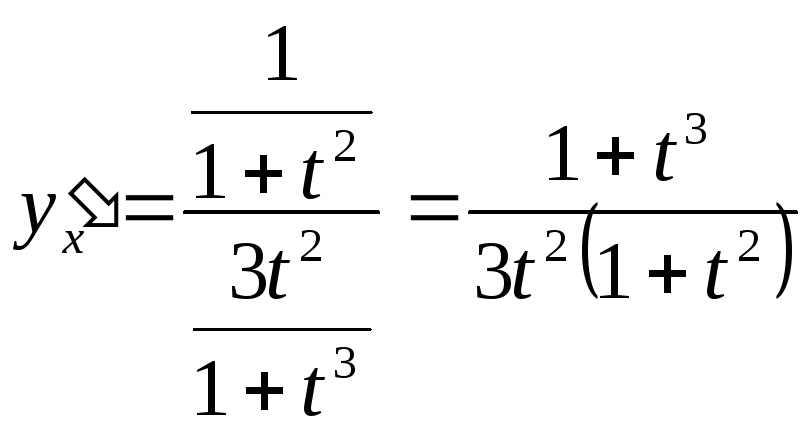 .
.
Подставим
![]() ,
получим:
,
получим:
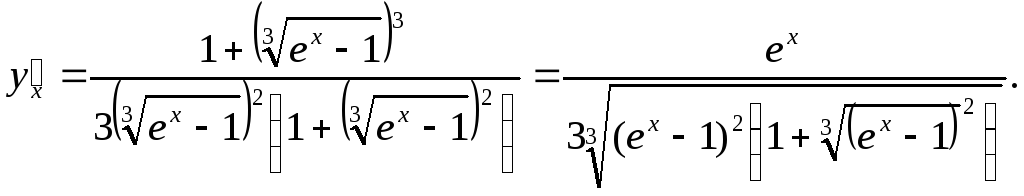
Пример 2
Вычислите значение
производной параметрически заданной
функции
![]() в точке
в точке
![]() Решение:
Функция
Решение:
Функция
![]() задана
параметрически. Дифференцируем её
используя формулу (6).
задана
параметрически. Дифференцируем её
используя формулу (6).
Вычисляем:
![]()
![]()
Подставим полученные выражения в формулу (14):
![]() .
.
Найдем значение производной в заданной точке.
Подставим значение
![]() в полученное выражение:
в полученное выражение:
![]() ,
т.е.
,
т.е.
![]() .
.
Пример 3
Вычислить
![]() ,
используя возможные способы:
,
используя возможные способы:
1)
![]() ;
;
Решение.
1. Данное уравнение задает неявно функцию
![]() .
Продифференцируем её двумя способами:
.
Продифференцируем её двумя способами:
I
способ.
Выразим из уравнения
![]() через
через
![]() :
:
![]() ,
,
![]() ,
,
![]()
![]() .
.
Продифференцируем
выражения по переменной
![]() :
:
![]()
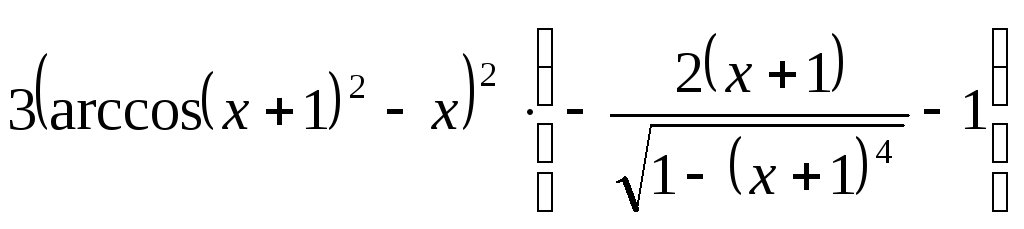 .
.
II
способ.
Продифференцируем
обе части уравнения по переменной
![]() ,
считая, что
,
считая, что
![]() есть функция от
есть функция от
![]() :
:
![]()
![]()
Откуда выразим
![]() :
:
![]() ;
;
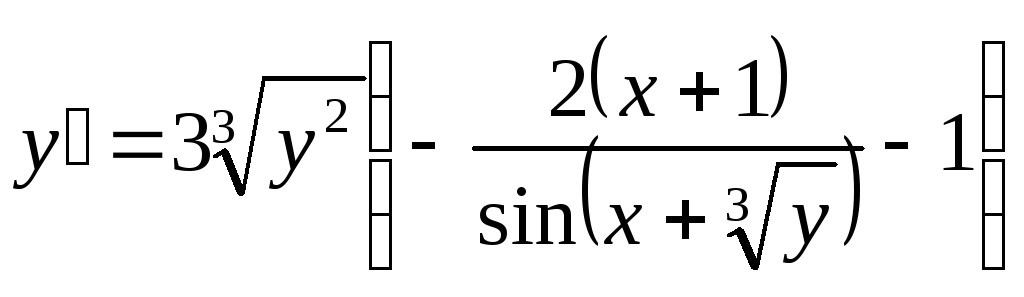 .
.
2.
![]() .
.
Функция
![]() задана неявно в данном случае невозможно
выразить переменную
задана неявно в данном случае невозможно
выразить переменную
![]() через
через
![]() ,
поэтому дифференцируем обе части
равенства, учитывая, что y
есть функция аргумента x:
,
поэтому дифференцируем обе части
равенства, учитывая, что y
есть функция аргумента x:
![]()
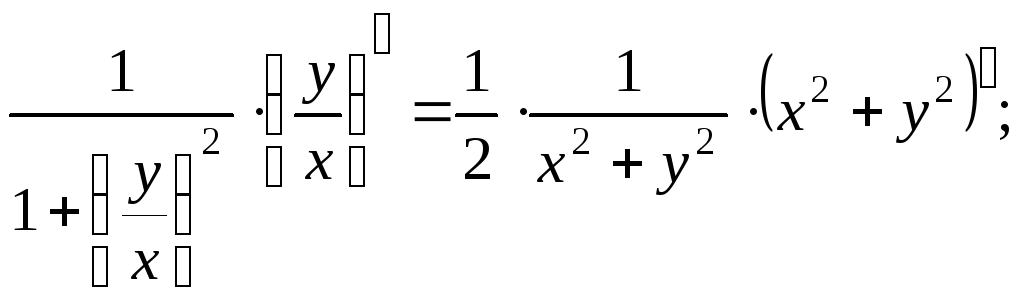
![]()
Из полученного
равенства выражаем![]()

Приходим к ответу:
![]()
Необходимое и достаточное условия
дифференцируемости функций. Дифференциал
функции
Пример 1.
Вычислить значение дифференциала
функции
![]() при
при
![]() и
и
![]()
Решение.
Дифференциал функции вычислим по формуле
(9). Найдем
![]() :
:
![]()
Найдем
![]() .
.
![]()
![]()
Подставляя найденные значения в формулу, получим,
![]()
Пример 2. Вычислить дифференциал функции:
1)
![]() 2)
2)
 3)
3)
![]()
Решение.
1) Найдем
![]() ;
;
![]()
![]() .
.
Подставляем полученное выражение в формулу (10), получим:
Пример 3. Вычислить приближенно с помощью дифференциала значение выражения:
1)
![]() 2)
2)
![]() 3)
3)
![]()
Решение. 1)
Воспользуемся формулой (11) для функции
![]() при
при
![]() Считаем, что
Считаем, что
![]()
![]()
Вычислим
![]()
Найдем
![]()
![]()
Тогда:
![]()
Таким образом,
![]()
2) Будем находить
приближенное значение функции
![]() в точке
в точке
![]() по формуле (11). Обозначим
по формуле (11). Обозначим
![]() ,
откуда
,
откуда
![]() ,
,
![]()
Найдем значение
![]()
![]()
Вычислим производную
функции
![]()
![]() откуда
откуда
![]()
Подставив найденные
значения в формулу (11)б получим
![]()
Таким образом,
получим ответ
![]()
3) Необходимо найти
приближенное значение функции
![]() в точке
в точке
![]()
Представим
![]() откуда
откуда
![]()
![]()
Тогда
![]()
Поскольку
![]() то
то
![]()
Тогда по формуле (11), получим:
![]()
Итак,
![]()
Пример 4. Куб
со стороной
![]() м
увеличился на 0,05 своего объема. Вычислить
приближенно приращения ребра куба.
м
увеличился на 0,05 своего объема. Вычислить
приближенно приращения ребра куба.
Решение.
Объем куба со стороной a
вычисляется по формуле
![]() Поэтому первоначальный объем куба равен
Поэтому первоначальный объем куба равен
![]() По
условию приращение объема куба равно
0,05 всего объема, т. е.
По
условию приращение объема куба равно
0,05 всего объема, т. е.
![]()
Так как
![]() то
то
![]()
Дифференциал функции вычисляем по формуле (9), т. е.
![]() откуда
откуда
![]()
Вычислим значение
производной
![]() для
для
![]() :
:
![]()
Теперь найдем
![]()
Таким образом, ребро куба увеличилось приблизительно на 0,16 (м).
Производные и дифференциалы высшего порядка
Пример 1.
Вычислить
![]() для функции
для функции
![]() .
.
Решение. Необходимую производную удобно найти использую формулу Лейбница (13). Для производной 4-го порядка формула Лейбница примет вид:
![]()
Функцию
![]() представим в виде
представим в виде
![]() Введем обозначения:
Введем обозначения:
![]()
![]() .
Для функции
.
Для функции
![]() найдем производные:
найдем производные:
![]()
![]()
![]()
![]()
Аналогично для
функции
![]() получим:
получим:
![]()
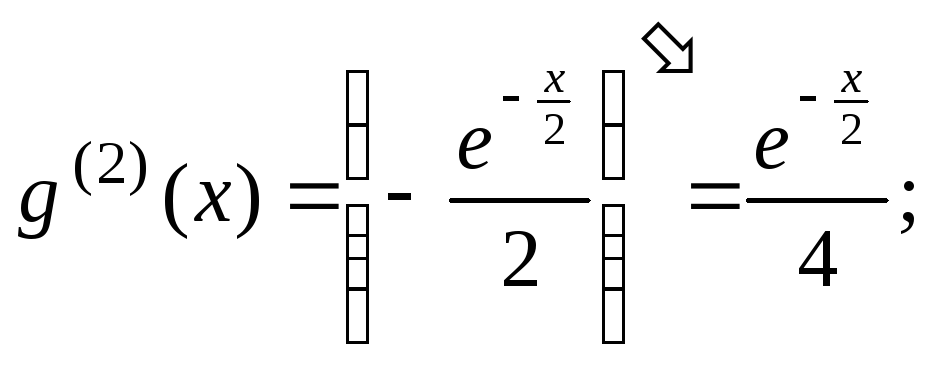
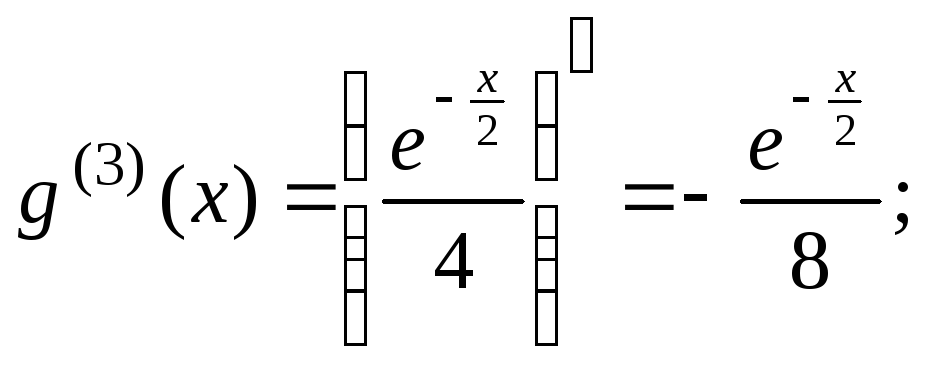
.
Правило Лопиталя. Формула Тейлора
Пример 1. Вычислить предел функции с помощью правила Лопиталя:
Решение.
1.
![]() Непосредственное вычисление предела
дает неопределенность вида
Непосредственное вычисление предела
дает неопределенность вида
![]() .
Поскольку условия теоремы 1 выполняются,
используем правило Лопиталя. По формуле
(17) имеем:
.
Поскольку условия теоремы 1 выполняются,
используем правило Лопиталя. По формуле
(17) имеем:

2. 2)
![]()
Непосредственное
вычисление предела дает неопределенность
вида
![]() ,
поэтому используем формулу (17):
,
поэтому используем формулу (17):

3. 3)
![]()
Имеем неопределенность
вида
![]() Поэтому, чтобы воспользоваться (17),
преобразуем выражение, стоящее под
знаком предела.
Поэтому, чтобы воспользоваться (17),
преобразуем выражение, стоящее под
знаком предела.
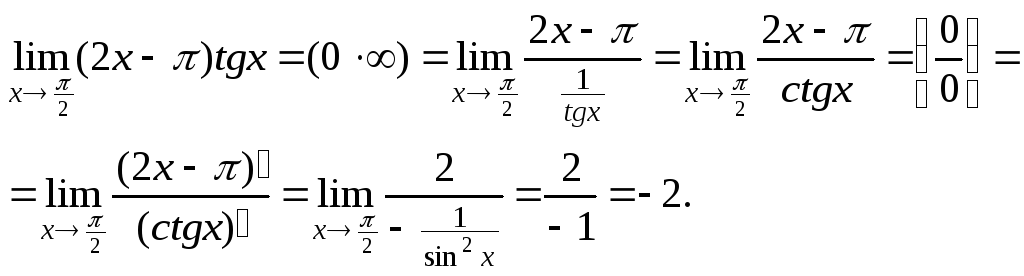
Исследование функций. Наибольшее
и наименьшее значение функций на промежутке
План исследования функции и построения графика
1. Найти область
определения
![]() функции
функции
![]() .
.
2. Найти область
значений
![]() (если это возможно вначале, часто
(если это возможно вначале, часто
![]() можно указать только по результатам
исследования).
можно указать только по результатам
исследования).
3. Исследовать функцию на четность.
4. исследовать на периодичность.
5. Найти точки пересечения с осями Ox (нули функции) и Oy.
6. Найти промежутки знакопостоянства функции.
7. Исследовать на непрерывность, дать классификацию разрывов.
8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).
9. Исследовать на монотонность и экстремум.
10. Исследовать на выпуклость, вогнутость, перегиб.
11. Построить график функции.
Пример 1.
Найти экстремумы функции
![]()
Решение. Подозрительными на экстремумы точками будут те, в которых производная функции либо равна нулю, либо не существует.
Найдем производную функции
![]()
Она определена для
любого
![]() .
.
Приравняем производную к нулю.
![]() ,
значит,
,
значит,
![]() Решая это уравнение, получим
Решая это уравнение, получим
![]() Областью определения функции является
числовая прямая. Воспользовавшись
теоремой 1, исследуем поведение функции
на промежутках
Областью определения функции является
числовая прямая. Воспользовавшись
теоремой 1, исследуем поведение функции
на промежутках
![]() ,
,
![]() ,
,
![]() .
.
Для этого определим
знак производной, т. е. выражения
![]() Очевидно, что для всякого
Очевидно, что для всякого
![]() выполняется неравенство
выполняется неравенство
![]() поэтому знак выражения
поэтому знак выражения
![]() зависит от знака квадратичного выражения
зависит от знака квадратичного выражения
![]() (рис. 4).
(рис. 4).

Рис. 4.
Так как при «переходе»
через точку с абсциссой
![]() производная
производная
![]() меняет знак с «+» на «–», то, согласно
теореме 1, в этой точке функция достигает
максимума. Максимум функции равен
значению функции в точке
меняет знак с «+» на «–», то, согласно
теореме 1, в этой точке функция достигает
максимума. Максимум функции равен
значению функции в точке
![]() :
:
![]()
Итак, максимум
функции равен
![]()
При «переходе»
через точку
![]() производная
производная
![]() меняет знак с «–» на «+». Поэтому в данной
точке функция достигает минимума.
меняет знак с «–» на «+». Поэтому в данной
точке функция достигает минимума.
Вычислим
значение функции в точке
![]() :
:
![]()
Итак, локальный
минимум функции равен
![]()
Пример 4.
Исследовать
функцию
![]() и построить ее график.
и построить ее график.
Решение. Исследование функции произведем согласно указанному выше плану.
1. Область определения функции:
![]()
2. Область значений E(f) укажем по результатам исследования.
3. Исследуем функцию на четность и нечетность.
![]()
Функция не является четной и нечетной.
4. Функция непериодическая.
5. Найдем точки пересечения графика с координатными осями.
Если у = 0,
т. е.
![]() то х = 1,
х = –3
– точки пересечения оси Ох
(нули функции).
то х = 1,
х = –3
– точки пересечения оси Ох
(нули функции).
Если х = 0, то у = 3 – точка пересечения оси Оу.
6. Найдем промежутки знакопостоянства функции. Используем метод интервалов (рис. 6).

Рис. 6.
Получаем:
![]() если
если
![]()
![]() если
если
![]()
7. Функция непрерывна на всей числовой оси.
8. Асимптот нет.
9. Исследуем функцию
на монотонность и экстремум. Найдем
![]()
![]()
Производная
существует
![]() Критическими точками являются те, для
которых
Критическими точками являются те, для
которых
![]() т. е.
т. е.
![]() и
и
![]()
Исследуем знак производной для конкретных промежутков, на которые критические точки делят числовую ось (рис. 7).

Рис. 7
Согласно теореме
1, функция возрастает на множестве
![]() и убывает на
и убывает на
![]() что схематически показано на рис. 7. В
точке
что схематически показано на рис. 7. В
точке
![]() она имеет локальный максимум, а в точке
х = 1
– минимум. Найдем их значения:
она имеет локальный максимум, а в точке
х = 1
– минимум. Найдем их значения:
![]()
![]()
10. Исследуем график функции на выпуклость, вогнутость и перегиб. Вычислим производную 2-го порядка:
![]()
Если
![]() то
то
![]() т. е.
т. е.
![]() – критическая точка 2-го рода, иных нет.
– критическая точка 2-го рода, иных нет.
Имеем
![]() если
если
![]() и
и
![]() если
если
![]() (рис. 8).
(рис. 8).
Рис. 8
Значит, график
функции является выпуклым на
![]() и вогнутым на
и вогнутым на
![]() согласно теореме 6.
согласно теореме 6.
![]() – точка перегиба (теорема 7).
– точка перегиба (теорема 7).
11. Используя полученные данные, построим график функции (рис. 9).
Рис. 9
Заметим, что
![]()
Пример 5.
Исследовать функцию
![]() и построить ее график.
и построить ее график.
Решение
1. Область определения
![]()
2. Область значений E(f) укажем по результатам исследования.
3. Поскольку область определения D(f) функции не является множеством, симметричным относительно х = 0, то функция не является четной и нечетной.
4. Функция непериодическая.
5. График функции
не пересекает ось Ох,
так как
![]() для всех
для всех
![]()
Если х = 0,
то
![]() – точка пересечения оси Оу.
– точка пересечения оси Оу.
6. Для всех
![]() выполняется
выполняется
![]() т. е. функция знакоположительна.
т. е. функция знакоположительна.
7. Функция непрерывна на своей области определения, х = 2 – точка разрыва.
Исследуем характер разрыва.
Вычисляем односторонние пределы в точке х = 2.
![]()
![]()
Следовательно, х = 2 – точка разрыва II рода (бесконечный скачок).
8. Исследуем функцию на асимптоты. Поскольку
![]()
![]()
то у = 1 – горизонтальная асимптота.
Мы показали, что в точке х = 2 имеется бесконечный скачок, а поэтому х = 2 – вертикальная асимптота.
Ищем наклонную
асимптоту
![]()
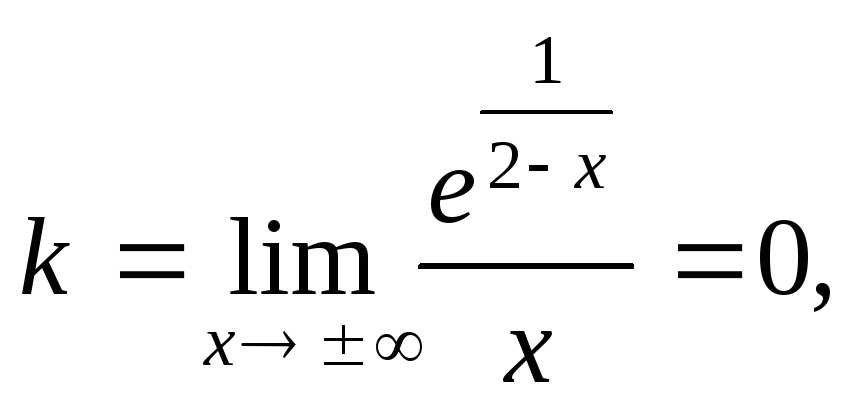
![]()
Получаем у = 1 – это горизонтальная асимптота. Наклонных асимптот нет.
9. Исследуем функцию на монотонность и экстремум.
Найдем производную функции:
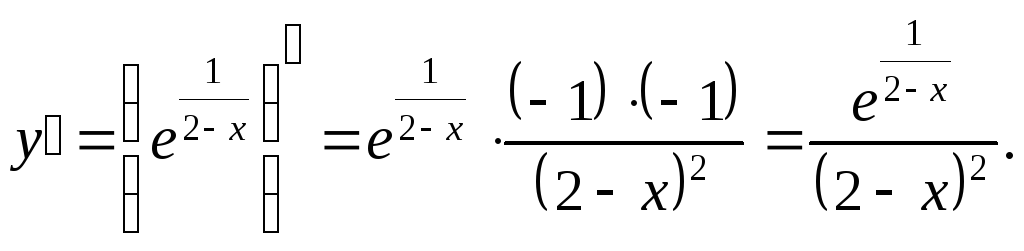
Производная положительна на всей D(f). Следовательно, функция возрастает всюду, где она определена. Экстремума нет.
10. Находим вторую производную:

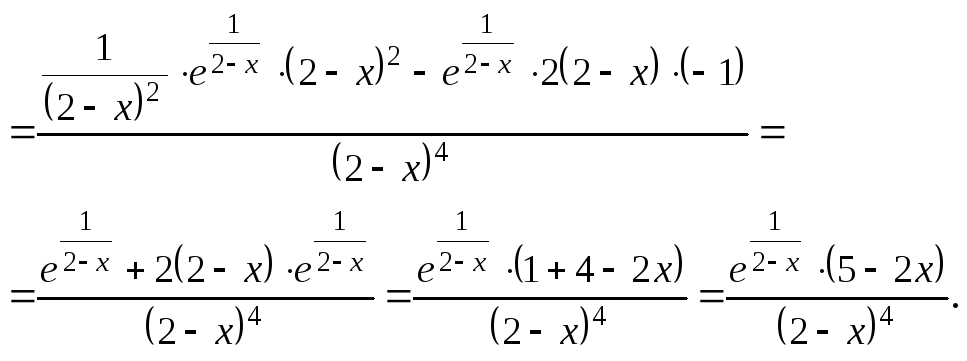
Поскольку
![]() и
и
![]() на D(f),
то знак производной 2-го порядка зависит
от знака выражения 5 – 2х.
Очевидно, что
на D(f),
то знак производной 2-го порядка зависит
от знака выражения 5 – 2х.
Очевидно, что
![]() если
если
![]() На этих промежутках график функции
вогнут.
На этих промежутках график функции
вогнут.
Если
![]() то
то
![]() т. е. график функции является выпуклым
на этом промежутке. Точка
т. е. график функции является выпуклым
на этом промежутке. Точка
![]() является точкой перегиба, так как при
этом значении вогнутость графика
изменяется на его выпуклость. Найдем
ординату, соответствующую точке перегиба:
является точкой перегиба, так как при
этом значении вогнутость графика
изменяется на его выпуклость. Найдем
ординату, соответствующую точке перегиба:
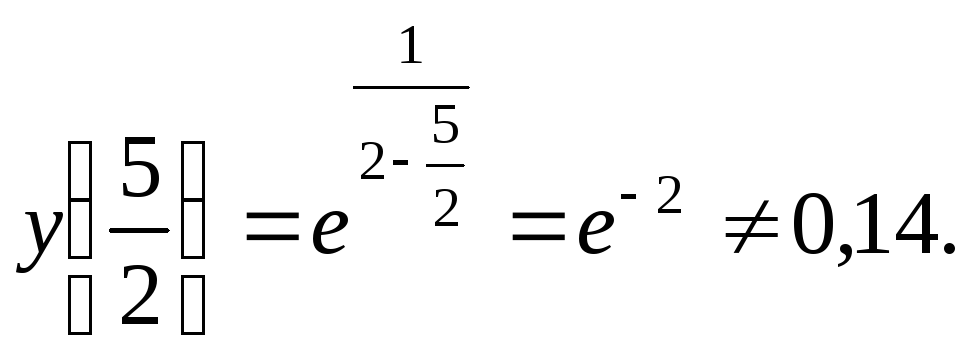
11. Используя результаты исследования, строим график функции (рис. 10).

Рис. 10
В дополнении
отметим, что
![]()
Дифференцирование функций
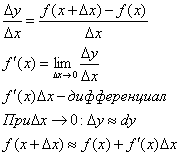
|
Инвариантность формы первого дифференциала:
|
|
Правила ДИФФЕРЕНЦИРОВАНИЯ:
|
|
Производная сложной функции:
|
|
Производная обратной функции:
|
Формулы дифференцирования
простейших функций:
|
|
|
|
|
|
ПРОИЗВОДНЫЕ ВЫСШИХ
ПОРЯДКОВ:
|
|
|
|
![]() – асимптота,
– асимптота,
если
![]()
![]()
Уравнение касательной к графику
функции в точке
![]()
![]()