
- •В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме, проекция вектора на ось
- •В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме
- •В.13 Векторное произведение
- •В.14 Смешанное произведение
- •Плоскость в пространстве
- •Прямая и плоскость в пространстве
- •. Поверхности второго порядка
- •Предел функции в точке и на бесконечности
- •II способ. Чтобы избавится от неопределенности вида , введем замену переменной , т.К. При получим .
- •. Односторонние пределы: Асимптоты графика функции.
- •Дифференцирование функции с переменной в основании степени и в показателе
- •Дифференцирование функций, заданных неявно и параметрически.
В.14 Смешанное произведение
Пример 1.
Векторы
![]()
![]()
![]() образуют правую тройку, взаимно
перпендикулярны и
образуют правую тройку, взаимно
перпендикулярны и
![]()
![]()
![]() Вычислить их смешанное произведение.
Вычислить их смешанное произведение.
Решение.
По определению,
![]() .
Вектор
.
Вектор
![]() образует с
образует с
![]() и
и
![]() правую тройку, причем
правую тройку, причем
![]()
![]() Значит
Значит
![]() Кроме того,
Кроме того,
![]()
Тогда
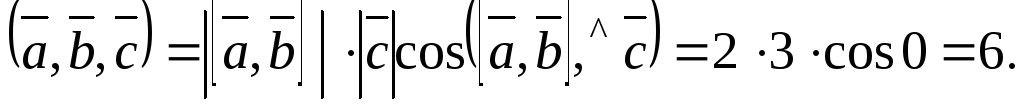
Пример 2.
Вычислить
![]() и определить ориентацию этой тройки
векторов, если
и определить ориентацию этой тройки
векторов, если
![]()
![]()
![]() Найти объем параллелепипеда, построенного
на векторах
Найти объем параллелепипеда, построенного
на векторах
![]()
![]()
![]() приведенных к общему началу.
приведенных к общему началу.
Решение.
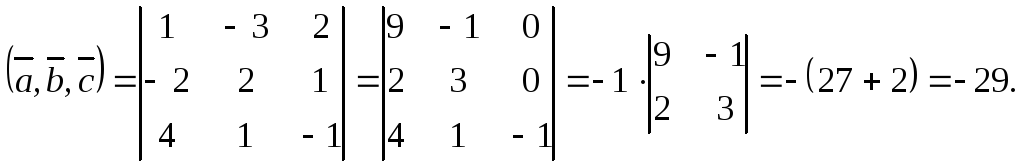
Поскольку смешанное
произведение отрицательно, тройка
векторов
![]()
![]()
![]() является левой. Находим объем
параллелепипеда:
является левой. Находим объем
параллелепипеда:
![]()
Пример 3. Доказать, что точки A(1, 2, –1), B(0, 1, 5), C(–1, 2, 1) и D(2, 1, 3) лежат в одной плоскости.
Решение. Рассмотрим три вектора
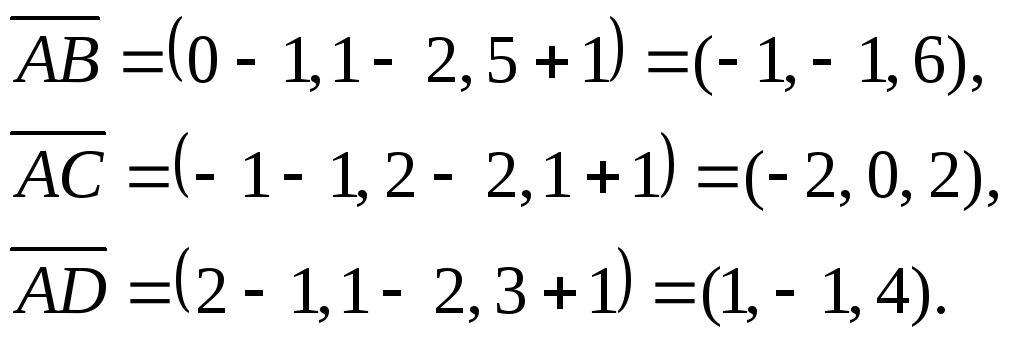
Согласно формуле (10) их смешанное произведение:
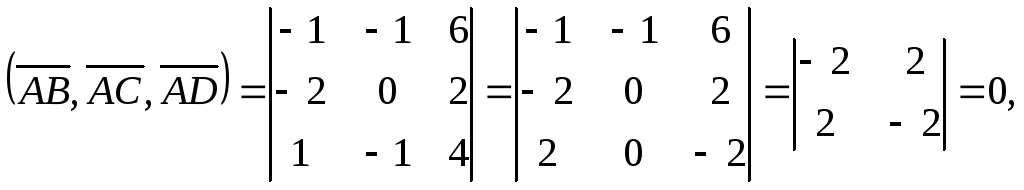
а это значит, что
векторы
![]() – компланарны и лежат в одной плоскости,
т. к. имеют общее начало. Таким образом,
точки A,
B,
C,
D
лежат в одной плоскости.
– компланарны и лежат в одной плоскости,
т. к. имеют общее начало. Таким образом,
точки A,
B,
C,
D
лежат в одной плоскости.
Пример
4.
Вычислить объем треугольной пирамиды
OABC,
если
![]()
![]()
![]()
Решение.
![]() ,
,
где
![]() – объем параллелепипеда, построенного
на векторах
– объем параллелепипеда, построенного
на векторах
![]()
Согласно геометрическому смыслу смешанного произведения
![]() .
.
Поскольку
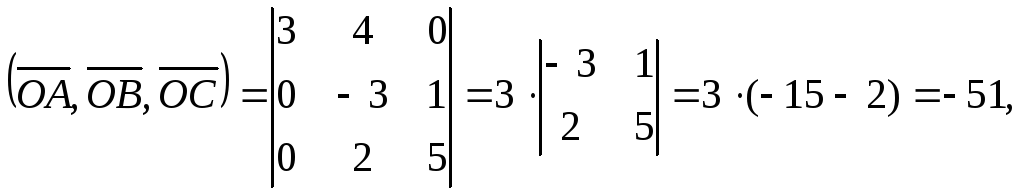
то получаем
![]()
Плоскость в пространстве
Пример
1.
Составить уравнение плоскости, проходящей
через точку
![]() ,
параллельно векторам
,
параллельно векторам
![]() и
и
![]() .
.
Решение.
Поскольку векторы
![]() и
и
![]() не коллинеарны (их координаты не являются
пропорциональными), то согласно (1),
составим уравнение:
не коллинеарны (их координаты не являются
пропорциональными), то согласно (1),
составим уравнение:
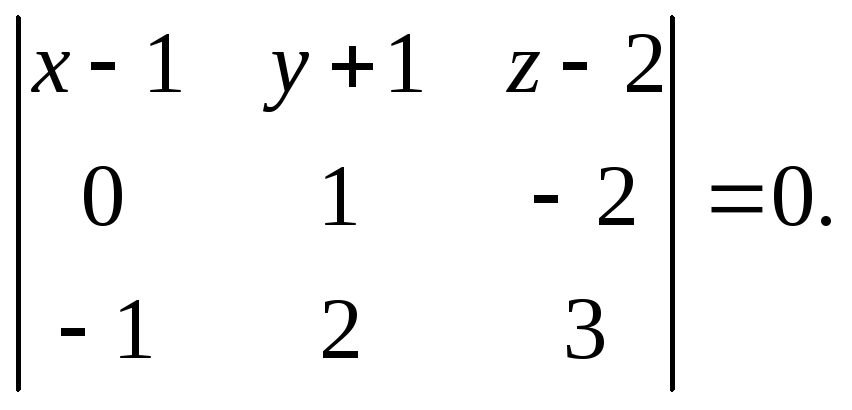
Преобразуем левую часть:
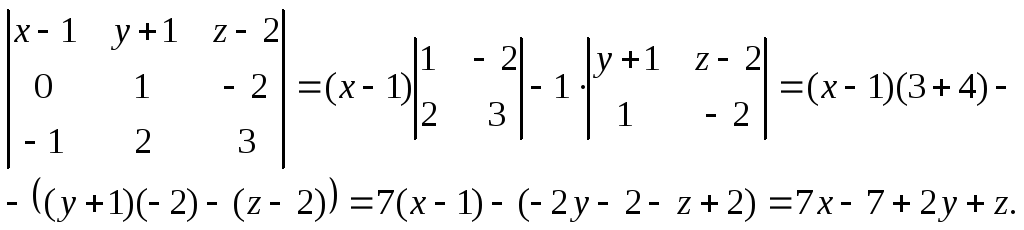
Таким образом общее уравнение искомой плоскости
![]()
Пример 2.
Составить уравнение плоскости P,
проходящей через точки
![]() и
и
![]() параллельно вектору
параллельно вектору
![]() .
.
Решение.
Векторы
![]() и
и
![]() неколлинеарны. Поэтому, согласно (1),
уравнение плоскости имеет вид
неколлинеарны. Поэтому, согласно (1),
уравнение плоскости имеет вид
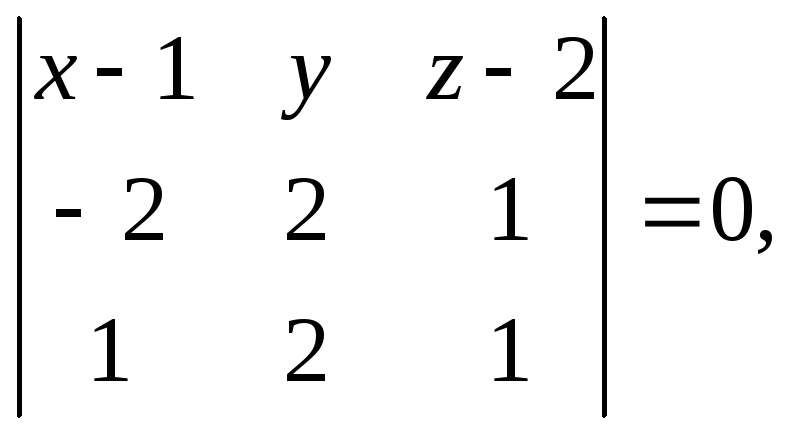 т. к. векторы
т. к. векторы
![]()
![]() и
и
![]() компланарны. Здесь
компланарны. Здесь
![]() Откуда получаем общее уравнение
Откуда получаем общее уравнение
![]()
Можно рассуждать
при построении уравнения также следующим
образом. В качестве нормального вектора
![]() плоскости P
может быть взят вектор
плоскости P
может быть взят вектор
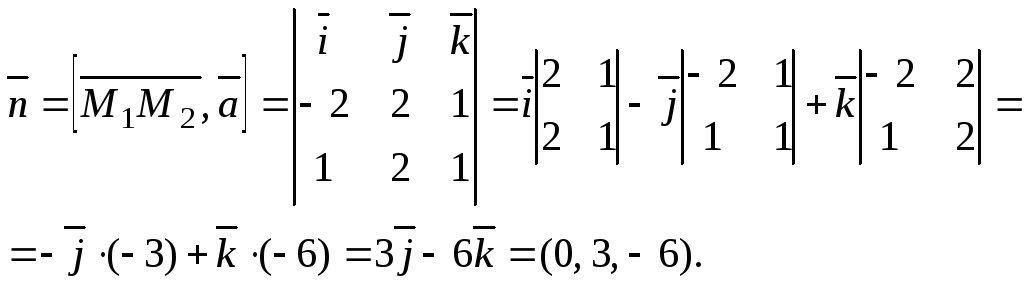
Тогда уравнение плоскости согласно формуле (2) примет вид:
![]() или
или
![]()
Пример
3.
Записать уравнение плоскости
![]()
1) «в отрезках»; 2) в параметрическом виде
Решение.
1) Перепишем уравнение плоскости в виде
![]() откуда после деления на –2 получим
искомое уравнение «в отрезках»:
откуда после деления на –2 получим
искомое уравнение «в отрезках»:
![]()
2) Из полученного
уравнения «в отрезках» имеем: точки
![]()
![]() и
и
![]() лежат в плоскости P.
тогда в качестве двух неколлинеарных
векторов
лежат в плоскости P.
тогда в качестве двух неколлинеарных
векторов
![]() и
и
![]() ,
параллельных плоскости P,
можно взять
,
параллельных плоскости P,
можно взять
![]() и
и
![]() Тогда векторно-параметрическое уравнение
плоскости примет вид
Тогда векторно-параметрическое уравнение
плоскости примет вид
![]() откуда в координатной форме получим:
откуда в координатной форме получим:
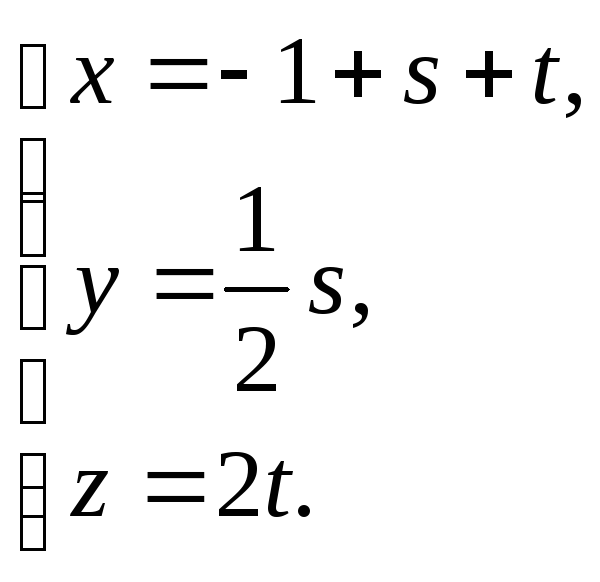
Это и есть параметрическое уравнение плоскости P.
Пример 4. Привести
к нормальному виду уравнение плоскости
![]()
Решение.
Так как свободный член уравнения
плоскости
![]() то нормирующий множитель
то нормирующий множитель
![]()
Тогда нормальным уравнением будет
![]()
Значит,
![]() а расстояние от начала координат до
плоскости равно 3.
а расстояние от начала координат до
плоскости равно 3.
Пример 5.
Составить уравнения плоскостей,
параллельных плоскости
![]() и отстоящих от нее на расстояние
и отстоящих от нее на расстояние
![]()
Решение.
Пусть
![]() – точка искомой плоскости. Тогда
– точка искомой плоскости. Тогда
![]() и
и
![]() Отсюда уравнения искомых плоскостей
Отсюда уравнения искомых плоскостей
![]() и
и
![]()
Пример 6.
Составить уравнение плоскости, проходящей
через точки A(1,
0, –1), B(1,
3, –4) и образующей угол
![]() с плоскостью
с плоскостью
![]()
Решение. Не ограничивая общности. Будем искать уравнение плоскости в виде
![]()
Поскольку точки A(1, 0, –1) и B(1, 3, –4) лежат в искомой плоскости, то их координаты удовлетворяют уравнению этой плоскости. Значит имеем
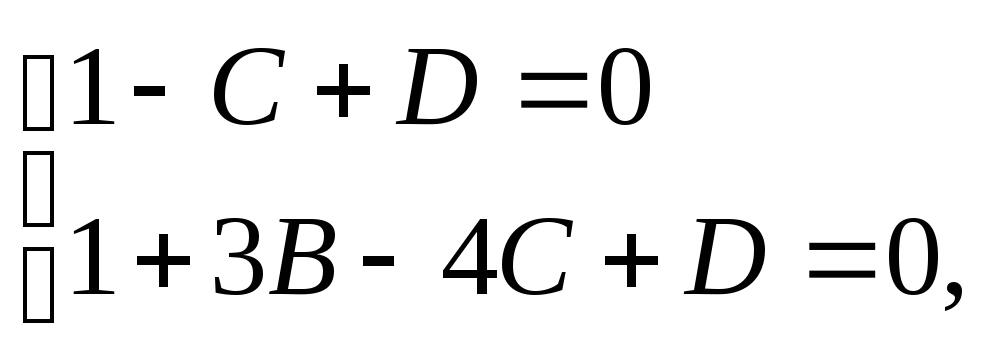
откуда
![]()
![]() Подставим найденные значения D
и B,
выраженные через C,
в уравнение плоскости:
Подставим найденные значения D
и B,
выраженные через C,
в уравнение плоскости:
![]()
Следовательно,
нормальный вектор
![]() .
.
Воспользуемся тем,
что плоскость образует угол
![]() с плоскостью
с плоскостью
![]() нормальный вектор
нормальный вектор
![]() которой
которой
![]() .
По формуле косинуса угла между плоскостями
имеем:
.
По формуле косинуса угла между плоскостями
имеем:
![]()
откуда
![]() или
или
![]() Находим C,
преобразовывая последнее равенство:
Находим C,
преобразовывая последнее равенство:
![]()
![]()
![]()
![]()
Имеем окончательно уравнение плоскостей:
![]()
Уравнение прямой в пространстве. Взаимное
расположение прямых
Пример 1. Составить канонические уравнения прямой:
1) проходящей через
точку
![]() параллельно вектору
параллельно вектору
![]()
2) проходящей через
две заданные точки
![]() и
и
![]()
3) заданной общими уравнениями
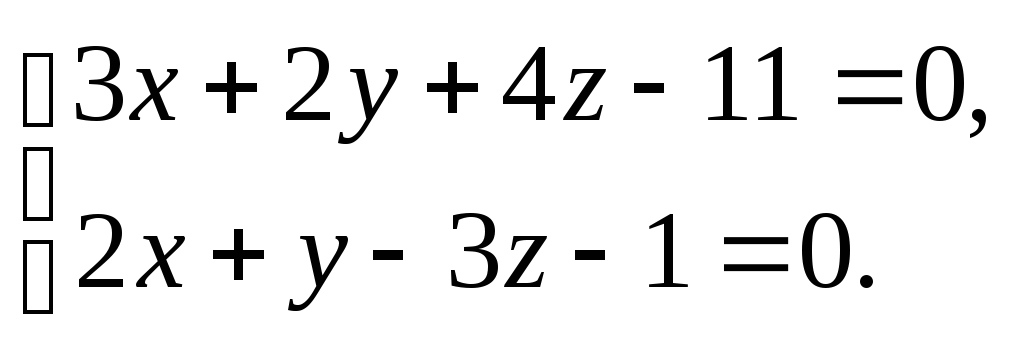
Решение.
1) Пусть
![]() – произвольная точка искомой прямой.
Тогда
– произвольная точка искомой прямой.
Тогда
![]() т. е. их координаты пропорциональны.
Т. к.
т. е. их координаты пропорциональны.
Т. к.
![]()
![]() то имеем соотношения:
то имеем соотношения:
![]()
которые и представляют собой канонические уравнения прямой с заданными свойствами на плоскости.
2) Пусть
![]() – произвольная точка прямой. Тогда
векторы
– произвольная точка прямой. Тогда
векторы
![]() и
и
![]() – коллинеарны, т. е. их координаты
пропорциональны.
– коллинеарны, т. е. их координаты
пропорциональны.
Т. к.
![]()
![]() то имеем:
то имеем:
![]()
Это и есть искомый результат.
3)
Для перехода от общих уравнений прямой
L
к каноническим обычно поступают следующим
образом. Подбирают какую-либо точку
![]() фиксируя числовые значения одной из
координат и решая относительно нее
систему двух линейных уравнений с двумя
неизвестными. Затем находят направляющий
вектор
фиксируя числовые значения одной из
координат и решая относительно нее
систему двух линейных уравнений с двумя
неизвестными. Затем находят направляющий
вектор
![]() прямой L
как векторное произведение нормальных
векторов плоскостей, задающих L.
Проиллюстрируем на примере.
прямой L
как векторное произведение нормальных
векторов плоскостей, задающих L.
Проиллюстрируем на примере.
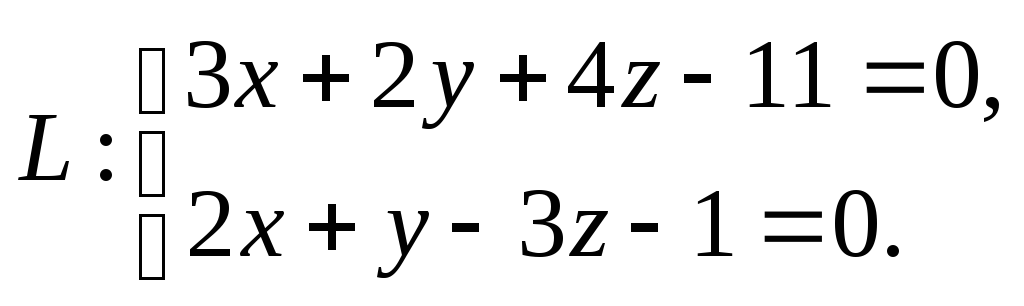
![]() – направляющий
вектор плоскости
– направляющий
вектор плоскости
![]() ,
,
![]() – нормальный вектор плоскости
– нормальный вектор плоскости
![]()
Тогда вектор
![]() .
Определим его координаты:
.
Определим его координаты:
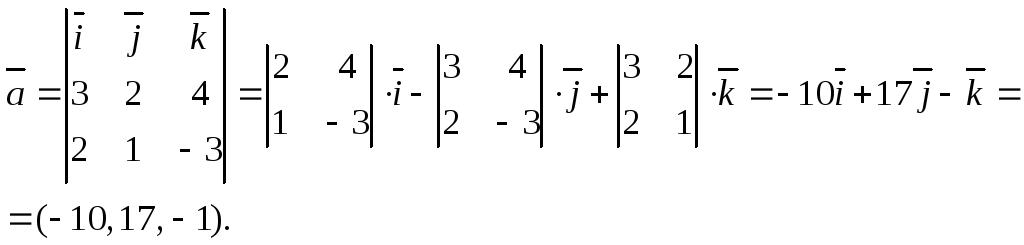
Для нахождения
точки
![]() зафиксируем одно из координатных
значений, например,
зафиксируем одно из координатных
значений, например,
![]() Тогда, подставив в заданные общие
уравнения
Тогда, подставив в заданные общие
уравнения
![]() получим:
получим:
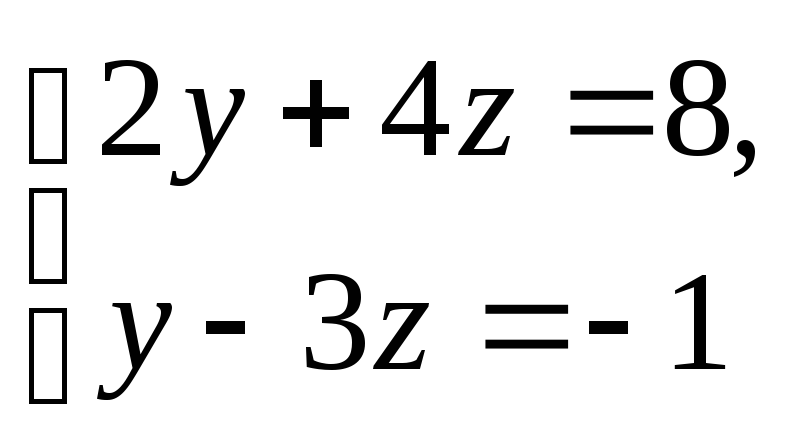 или
или
![]() т. е.
т. е.
![]() .
.
Таким образом, искомые канонические уравнения
![]()
Пример 2.
Докажите, что прямые
![]() и
и
![]() параллельны, и найдите расстояние между
ними, если они заданны параметрическими
уравнениями:
параллельны, и найдите расстояние между
ними, если они заданны параметрическими
уравнениями:
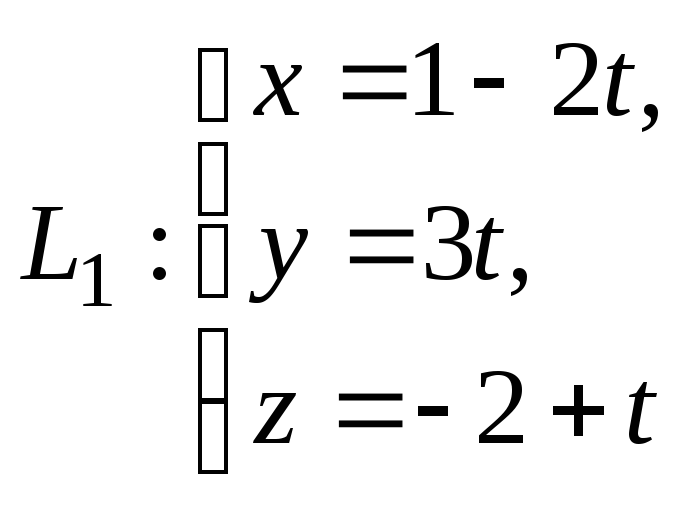 и
и
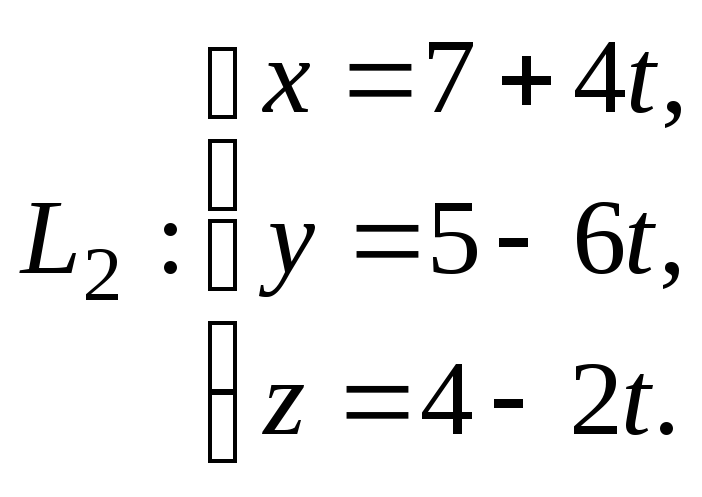
Решение.
Прямая
![]() имеет направляющий вектор
имеет направляющий вектор
![]() ,
а
,
а
![]() –
–
![]() причем
причем
![]() т. к.
т. к.
![]() Значит,
Значит,
![]()
Найдем расстояние
между ними, используя формулу расстояния
от точки до прямой.
![]()
![]() Тогда
Тогда
![]()
где
![]() и
и
![]() – радиус-векторы точек
– радиус-векторы точек
![]() и
и
![]() .
.

![]()
![]()
Значит,
![]()
Пример 3.
Докажите, что прямые
![]() и
и
![]() пересекаются, и найдите координаты
точки пересечения, если они заданны
параметрическими уравнениями:
пересекаются, и найдите координаты
точки пересечения, если они заданны
параметрическими уравнениями:
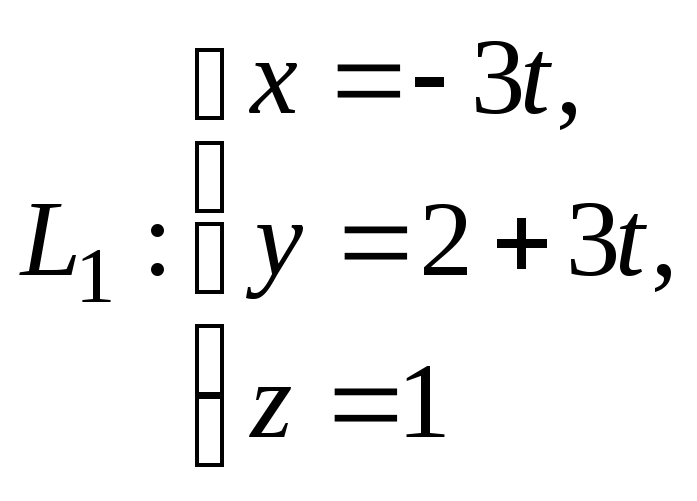 и
и
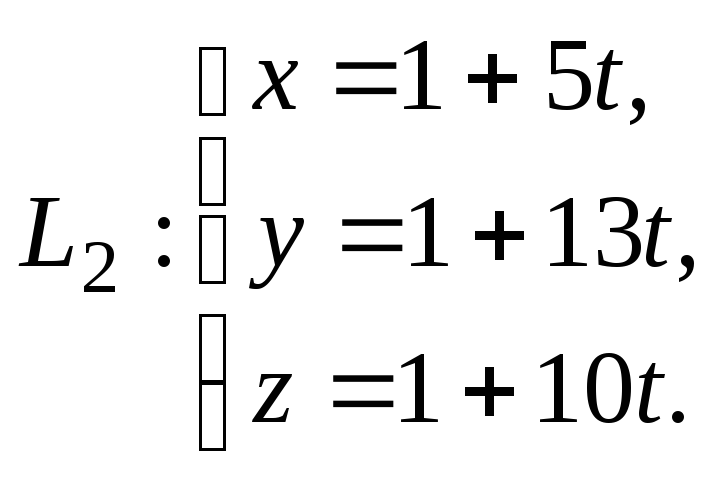
Решение.
![]()
![]() причем
причем
![]() .
Значит
.
Значит
![]() .
.
Прежде всего,
определим, лежат ли прямые в одной
плоскости, т. е. являются ли векторы
![]()
![]() и
и
![]() компланарными (здесь
компланарными (здесь
![]()
![]() ).
Найдем для этого их смешанное произведение:
).
Найдем для этого их смешанное произведение:
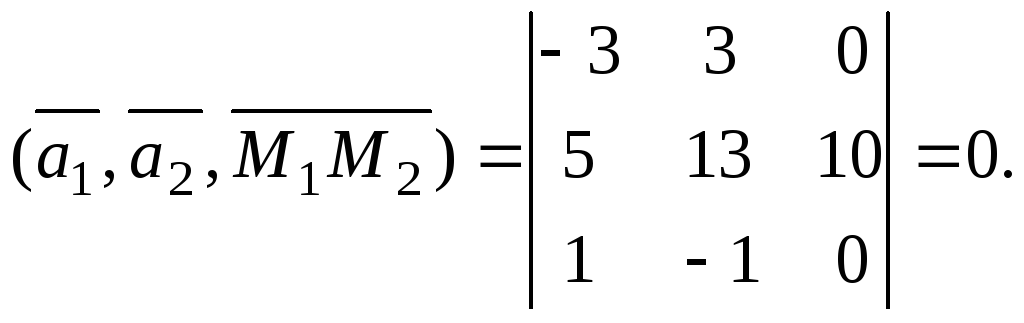
Значит, прямые лежат в одной плоскости и не параллельны. Следовательно они пересекаются.
Найдем их точку
пересечения
![]() .
.
 при подстановке в
уравнение
при подстановке в
уравнение
![]() .
.
Значит,
![]()
![]() Итак,
Итак,
![]()
Пример 4.
Докажите, что прямые
![]() и
и
![]() скрещиваются, и найдите расстояние
между ними, если они заданы параметрическими
уравнениями:
скрещиваются, и найдите расстояние
между ними, если они заданы параметрическими
уравнениями:
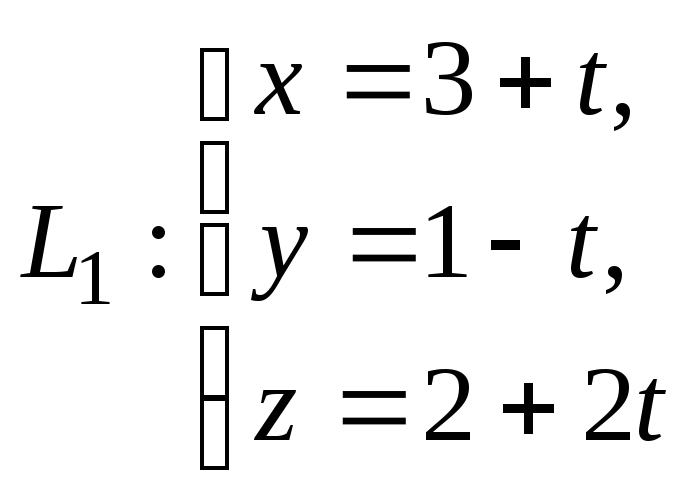 и
и
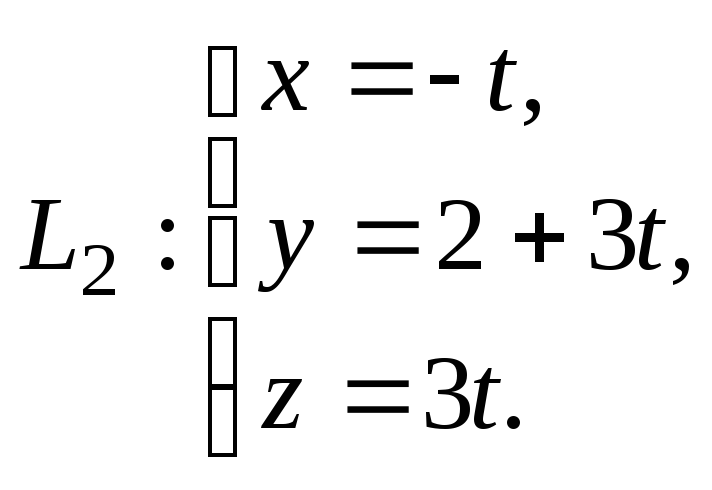
Решение.
![]()
![]() причем
причем
![]() .
Значит
.
Значит
![]() .
Определим, компланарны ли они. Т. к.
.
Определим, компланарны ли они. Т. к.
![]()
![]() то условием компланарности прямых
служит компланарность векторов
то условием компланарности прямых
служит компланарность векторов
![]()
![]() и
и
![]() .
Найдем смешанные произведения этих
векторов:
.
Найдем смешанные произведения этих
векторов:
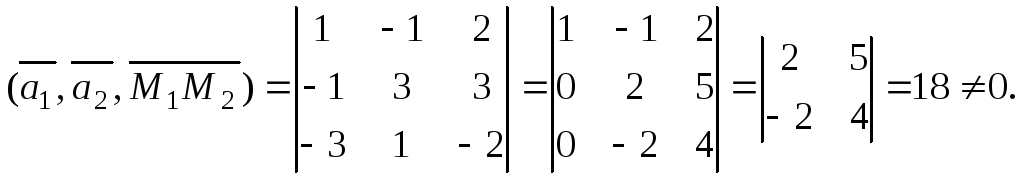
Значит, указанные
векторы, а вместе с ними и прямые
![]() и
и
![]() не лежат в одной плоскости.
не лежат в одной плоскости.
Прямые
![]() и
и
![]() скрещиваются, т. к. они не пересекаются
и не параллельны. Найдем расстояние
между ними по формуле:
скрещиваются, т. к. они не пересекаются
и не параллельны. Найдем расстояние
между ними по формуле:
![]()
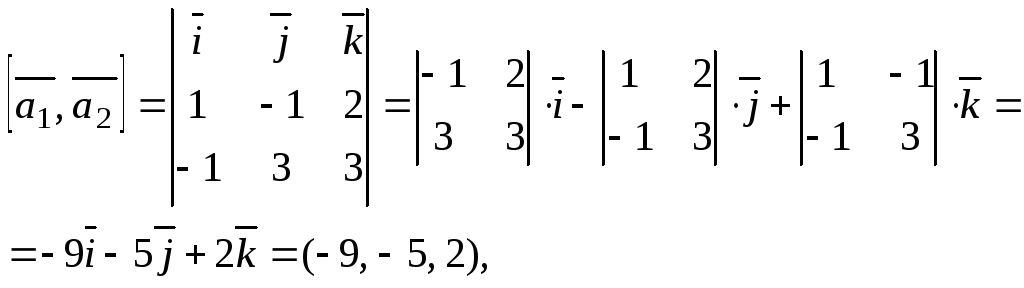
![]()
Итак,
![]()
