
- •В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме, проекция вектора на ось
- •В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме
- •В.13 Векторное произведение
- •В.14 Смешанное произведение
- •Плоскость в пространстве
- •Прямая и плоскость в пространстве
- •. Поверхности второго порядка
- •Предел функции в точке и на бесконечности
- •II способ. Чтобы избавится от неопределенности вида , введем замену переменной , т.К. При получим .
- •. Односторонние пределы: Асимптоты графика функции.
- •Дифференцирование функции с переменной в основании степени и в показателе
- •Дифференцирование функций, заданных неявно и параметрически.
. Односторонние пределы: Асимптоты графика функции.
Пример 1.
Найти односторонние пределы функции
![]() в точке
в точке
![]() :
:
1)
![]() ,
,
![]() ; 2)
; 2)
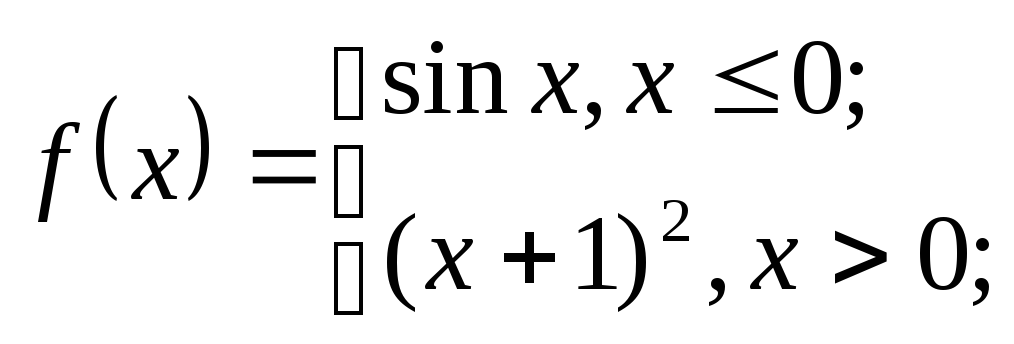
![]()
Решение.
1. Вычислим
пределы функции в точке
![]() слева и справа, т.е.
слева и справа, т.е.
![]() и
и
![]() .
.
При
![]()
![]()
![]()
![]() .
.
Значит
![]() .
.
При
![]()
![]()
![]()
![]() .
.
Значит
![]() .
.
2. При
![]() функция
задана формулой
функция
задана формулой
![]() .
.
Поэтому
![]() ,
,
При
![]() функция задана формулой
функция задана формулой
![]() т.е.
т.е.
![]()
Значит
![]() .
.
Пример 2. С
помощью односторонних предметов
показать, что функция
![]() не имеет предела в точке.
не имеет предела в точке.
Решение. При
![]() имеем
имеем
![]() и функция принимает вид
и функция принимает вид
![]() .
.
Поэтому
![]() .
.
При
![]() имеем
имеем
![]() и функцию
и функцию
![]() .
.
Поэтому
![]() .
.
Получим, что оба
односторонних предела функции в точке
![]() существуют,
однако они различны, поэтому
существуют,
однако они различны, поэтому
![]() не существует.
не существует.
Пример 3. Найти
асимптоты графика функции
![]() .
.
Решение.
Вертикальных
асимптот данная функция не имеет, потому
что она определена для любых
![]() .
Для того чтобы найти горизонтальные
асимптоты надо рассмотреть пределы
функции на бесконечности:
.
Для того чтобы найти горизонтальные
асимптоты надо рассмотреть пределы
функции на бесконечности:
![]() .
.
Получили, что
![]() – горизонтальная асимптота (ось
– горизонтальная асимптота (ось
![]() ).
).
Будем искать
наклонные асимптоты в виде
![]() .
.
Согласно формулам (25), (26) вычисляем:
![]() .
.
Так как
![]() ,
значит наклонных асимптот у графика
нет.
,
значит наклонных асимптот у графика
нет.
Пример 4. Найти асимптоты графика функции
![]() .
.
Решение.
Так как при
![]() функция не определена, рассмотрим:
функция не определена, рассмотрим:
![]() и
и
![]()
Вычисляем:
![]() ;
;
![]()
Поэтому прямая
![]() является вертикальной асимптотой
графика функции.
является вертикальной асимптотой
графика функции.
Ищем горизонтальную асимптоту. Поскольку
![]() ,
,
то горизонтальных асимптот нет.
Выясним наличие наклонных асимптот. По формулам (25) и (26) находим
![]()
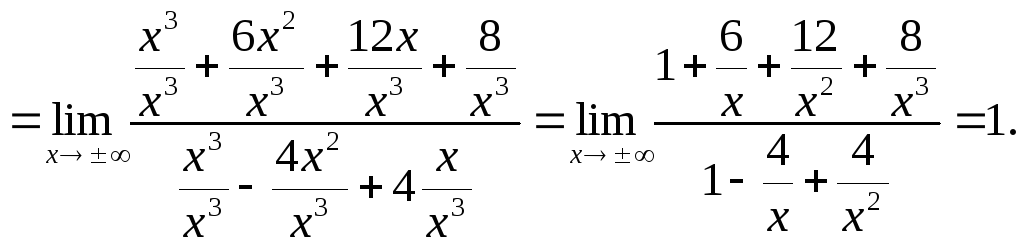
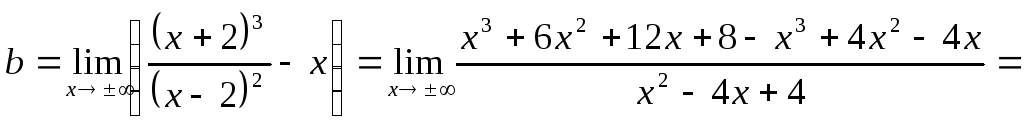
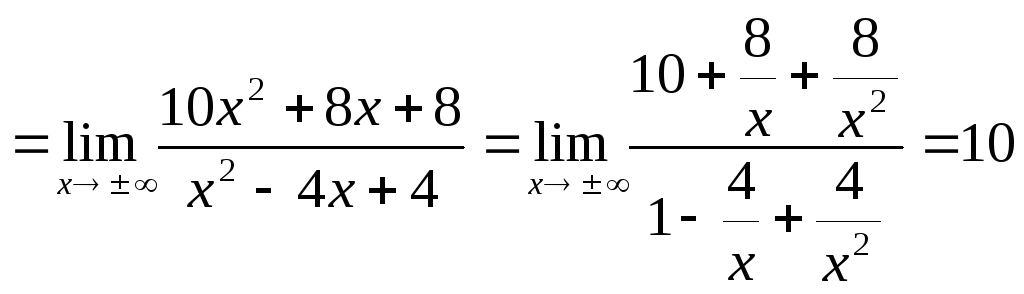 .
.
Получим, что
![]() – наклонная асимптоты.
– наклонная асимптоты.
. Непрерывность функции. Классификация
точек разрыва.
Пример 1. Пользуясь
определением непрерывности доказать,
что функция
![]() непрерывна всюду на
непрерывна всюду на
![]() .
.
Решение. Докажем
непрерывность этой функции в произвольной
точке
![]() .
.
Пусть
![]() – приращение аргумента в точке
– приращение аргумента в точке
![]() .
Соответствующее приращение функции
имеет вид:
.
Соответствующее приращение функции
имеет вид:
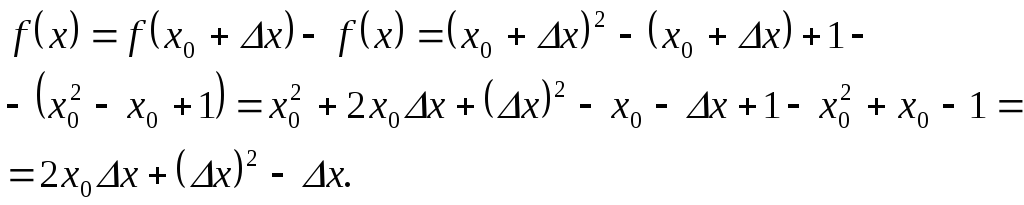
Вычислим предел приращения функции, когда приращение аргумента стремится к нулю:
![]()
![]()
![]()
![]() .
.
Получили, что
![]() ,
что и означает непрерывность функции
,
что и означает непрерывность функции
![]() на всей числовой прямой, т.к.
на всей числовой прямой, т.к.
![]() – произвольная действительная точка.
– произвольная действительная точка.
Пример 2.
Найти точки разрыва функции
![]() и исследовать их характер. Построить
схематический чертеж графиков этих
функций в окрестности точек разрыва
и исследовать их характер. Построить
схематический чертеж графиков этих
функций в окрестности точек разрыва
1)
![]() ;
;
Решение. Функция
![]() определена на всей числовой прямой,
кроме
определена на всей числовой прямой,
кроме
![]() .
Данная
функция является элементарной,
следовательно она является непрерывной
в каждой точке своей области определения.
Поэтому единственной точкой разрыва
является точка
.
Данная
функция является элементарной,
следовательно она является непрерывной
в каждой точке своей области определения.
Поэтому единственной точкой разрыва
является точка
![]() ,
в которой функция не определена. Для
определения типа разрыва в этой точке
вычислим односторонние пределы функции:
,
в которой функция не определена. Для
определения типа разрыва в этой точке
вычислим односторонние пределы функции:
![]() ;
; ![]() .
.
Приходим к выводу,
что
![]() – точка разрыва II
рода (бесконечного скачка).
– точка разрыва II
рода (бесконечного скачка).
График функции
![]() в
окрестности точки
в
окрестности точки
![]() представлен на
представлен на
2.
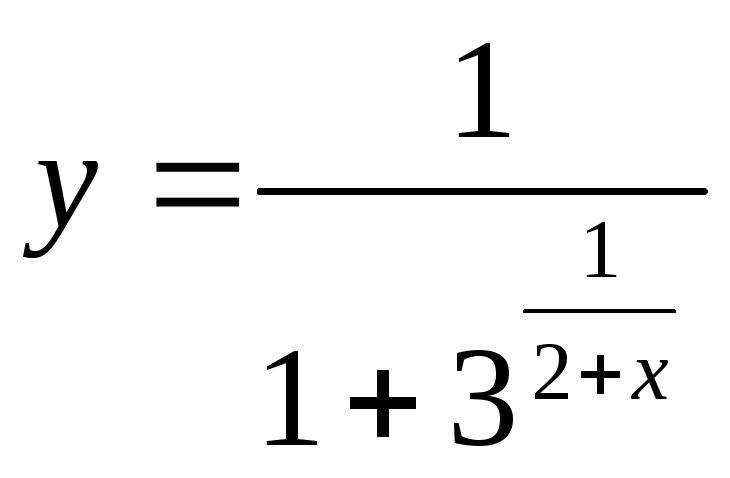 .Точкой
разрыва данной функции является точка
.Точкой
разрыва данной функции является точка
![]() .
.
Вычислим односторонние
пределы заданной функции в точке
![]() .
.
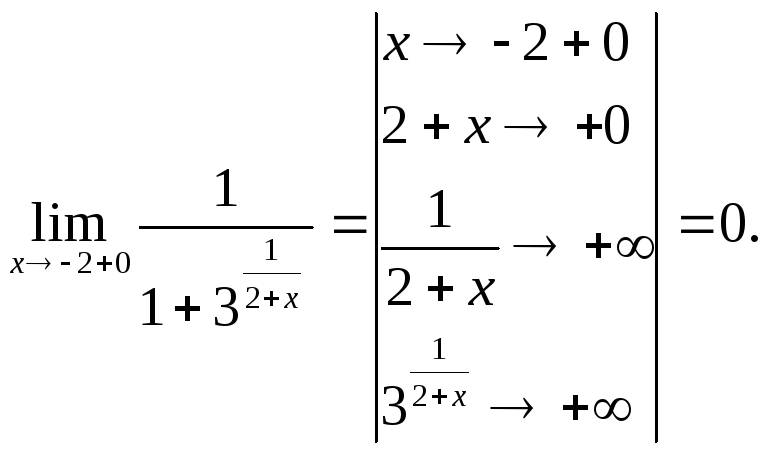
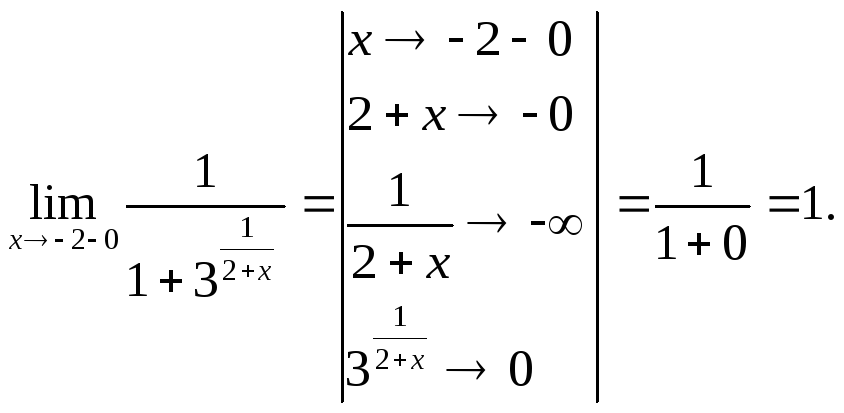
Получили, что оба
односторонних предела существуют (и
конечны), но не равны между собой. Поэтому
![]() – точка разрыва I
рода (скачка) – рис.2. Заметим, что скачок
равен:
– точка разрыва I
рода (скачка) – рис.2. Заметим, что скачок
равен:
![]() .
.
Пример 3. Дана
функция
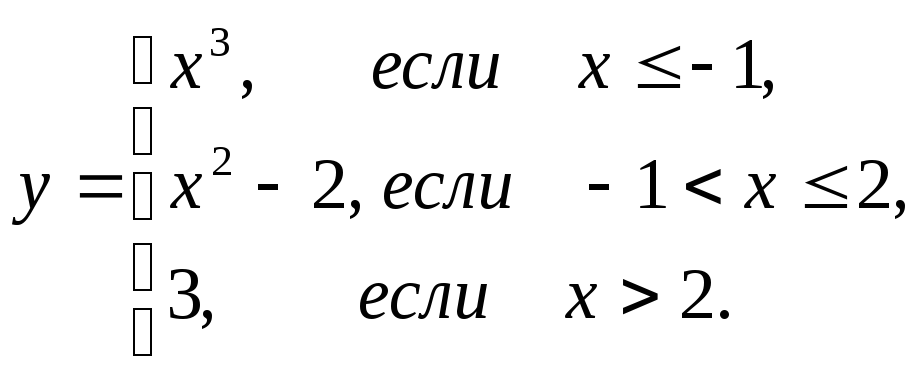
![]()
Исследовать ее на непрерывность и разрыв. Построить график.
Решение.
На промежутках
![]() заданы аналитические выражения
элементарных функций, которые определены
и, следовательно, непрерывны на каждом
промежутке. Поэтому точками «подозрительными
на разрыве», являются точки
заданы аналитические выражения
элементарных функций, которые определены
и, следовательно, непрерывны на каждом
промежутке. Поэтому точками «подозрительными
на разрыве», являются точки
![]() и
и
![]() .
.
Вычислим односторонние
пределы функции в точке
![]() .
.
Так как
![]() при
при
![]() ,
то
,
то
![]() .
.
Так как
![]() при
при
![]() ,
то
,
то
![]() .
.
Вычислим значение
функции в точке
![]() :
:
![]() .
.
Получим, что
выполнены условия непрерывности функции
в точке
![]() .
Поэтому в точке
.
Поэтому в точке
![]() разрыва функции нет.
разрыва функции нет.
Вычислим односторонние
пределы функции в точке
![]() .
.
Так как
![]() при
при
![]() ,
то
,
то
![]() .
.
Так как
![]() при
при
![]() ,
то
,
то
![]() .
.
Получили, что
![]() – точка разрыва I
рода (скачка). Значит, функция непрерывна
всюду на числовой прямой кроме точки.
– точка разрыва I
рода (скачка). Значит, функция непрерывна
всюду на числовой прямой кроме точки.
![]() в которой она имеет скачок, равный 1.
в которой она имеет скачок, равный 1.
