- •В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме, проекция вектора на ось
- •В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме
- •В.13 Векторное произведение
- •В.14 Смешанное произведение
- •Плоскость в пространстве
- •Прямая и плоскость в пространстве
- •. Поверхности второго порядка
- •Предел функции в точке и на бесконечности
- •II способ. Чтобы избавится от неопределенности вида , введем замену переменной , т.К. При получим .
- •. Односторонние пределы: Асимптоты графика функции.
- •Дифференцирование функции с переменной в основании степени и в показателе
- •Дифференцирование функций, заданных неявно и параметрически.
Предел функции в точке и на бесконечности
Пример 1. Пользуясь определением предела функции в точке по Коши, доказать, что
![]()
Решение.
Зафиксируем
произвольное значение
![]()
Согласно определению,
требуется по
найти такое число
![]() чтобы
из условия
чтобы
из условия
![]() следовало неравенство (2), которое в
данном случае имеет вид
следовало неравенство (2), которое в
данном случае имеет вид
![]() (6)
(6)
Упрощая последнее неравенство, получим
![]()
![]()
![]()
![]()
![]()
Следовательно,
если принять
![]() то из неравенства
то из неравенства
![]()
![]() будет следовать неравенство (6). Это и
означает, что
будет следовать неравенство (6). Это и
означает, что
![]()
Пример 2.
Вычислить
![]()
Решение.
Представим функцию
![]() как произведение двух функций
как произведение двух функций
![]() и
и
![]()
Функция
![]() является суммой двух бесконечно малых
функций при
является суммой двух бесконечно малых
функций при
![]() так как
так как
![]() и
и
![]() Значит
Значит
![]() – бесконечно малая при
– бесконечно малая при
![]()
Функция
![]() является ограниченной, так как значения
этой функции будут лежать в промежутке
является ограниченной, так как значения
этой функции будут лежать в промежутке
![]()
Получаем произведение
бесконечно малой
![]() на ограниченную
на ограниченную
![]()
Значит f(x)
– есть бесконечно малая при
![]() т. е.
т. е.
![]()
Пример 3. Вычислить предел функции в точке двумя способами: непосредственно и с помощью замены переменной:
![]()
Решение.
I
способ. При
подстановке в выражение, стоящее под
знаком предела значения
![]() получаем неопределенность
получаем неопределенность
![]() ,
для раскрытия которой разложим числитель
и знаменатель дроби на множители.
,
для раскрытия которой разложим числитель
и знаменатель дроби на множители.
![]() ,
,
![]() .
.
Подставив полученные выражения, получим:
![]() .
.
II способ. Чтобы избавится от неопределенности вида , введем замену переменной , т.К. При получим .
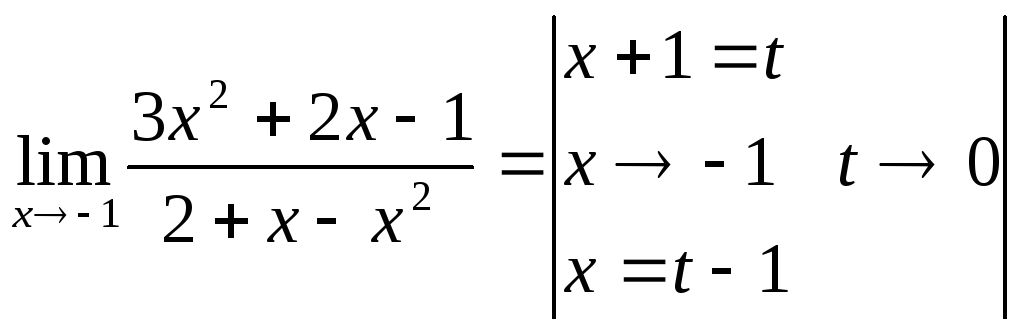 =
=![]()
![]() .
.
Замечательные пределы
Первый замечательный предел
![]() (7)
(7)
Как следствие формулы (7) справедливы формулы
![]()
![]()
![]()
Второй замечательный предел
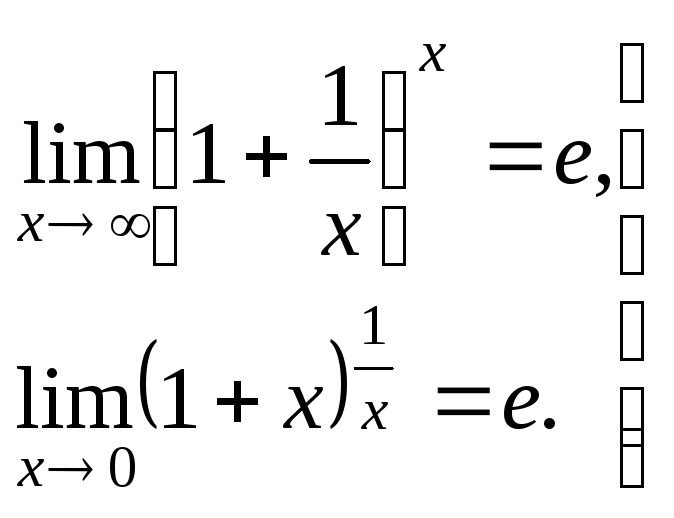 (8)
(8)
Третий
замечательный предел
![]() (9)
(9)
в частности,
![]()
Четвертый замечательный предел
![]() (10)
(10)
в частности,
![]()
Пятый замечательный предел
![]() (11)
(11)
Указанные формулы
(7)–(11) замечательных пределов обобщаются
на любую функцию u(x),
стоящую вместо независимой переменной
х
при условии, что
![]() если
если
![]() (или
(или
![]() )
во всех формулах кроме (8), в которых
)
во всех формулах кроме (8), в которых
![]()
Обобщенная таблица замечательных пределов
![]() ;
;
![]() ;
;
![]() ;
(12)
;
(12)
![]() ;
;
![]() ;
(13)
;
(13)
![]() ;
;
![]() ;
(14)
;
(14)
![]() . (15)
. (15)
При использовании
обобщенных форму на практике вместо
![]()
![]() (под
знаком предела пишут указанное в условии:
(под
знаком предела пишут указанное в условии:
![]() .
.
Все приведенные
формулы обобщенной таблицы замечательных
пределов (кроме формул (12)) раскрывают
неопределенность типа
![]() .
Формулы (12) раскрывают неопределенность
типа
.
Формулы (12) раскрывают неопределенность
типа
![]() .
.
Пример 1. Вычислить предел функций в точке:
Решение.
1. 1)
![]() ;
При непосредственной подстановке
в функцию значения
;
При непосредственной подстановке
в функцию значения
![]() получаем неопределенность вида
получаем неопределенность вида
![]() ,
для раскрытия которой воспользуемся
первым замечательным пределом.
,
для раскрытия которой воспользуемся
первым замечательным пределом.
![]() 2. 2)
2. 2)
![]() ;
При
;
При
![]() получаем неопределенность
получаем неопределенность
![]() ,
для раскрытия которой сначала применим
формулы тригонометрии, а затем первый
замечательный предел.
,
для раскрытия которой сначала применим
формулы тригонометрии, а затем первый
замечательный предел.
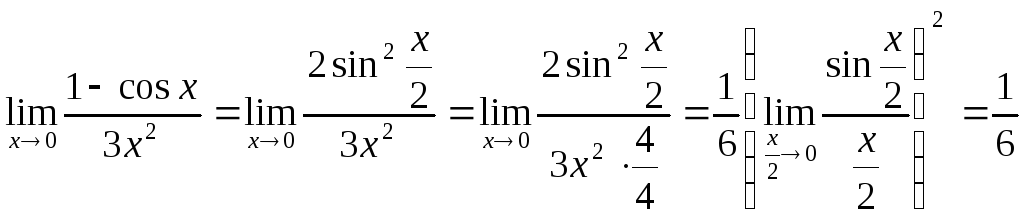 .
.
3. )
![]() Преобразуем вначале разность косинусов
в произведение, а затем используем 1-й
замечательный предел:
Преобразуем вначале разность косинусов
в произведение, а затем используем 1-й
замечательный предел:
![]()
=![]()
=![]()
Пример 2. Вычислить предел функции, используя обобщенную таблицу замечательных пределов.
ешение. 1.
1)
![]() ;
Воспользуемся второй формулой
из (12):
;
Воспользуемся второй формулой
из (12):
![]()
В данном случае
![]() и
и
![]() ,
если
,
если
![]() ,
,
значит
![]() .
.
2.
![]() ;
Непосредственная подстановка в функцию
значения
;
Непосредственная подстановка в функцию
значения
![]() дает неопределенность вида
дает неопределенность вида
![]() ,
для раскрытия которой воспользуемся
второй формулой из (12). Для этого
преобразуем выражение под знаком
предела.
,
для раскрытия которой воспользуемся
второй формулой из (12). Для этого
преобразуем выражение под знаком
предела.
![]()
=
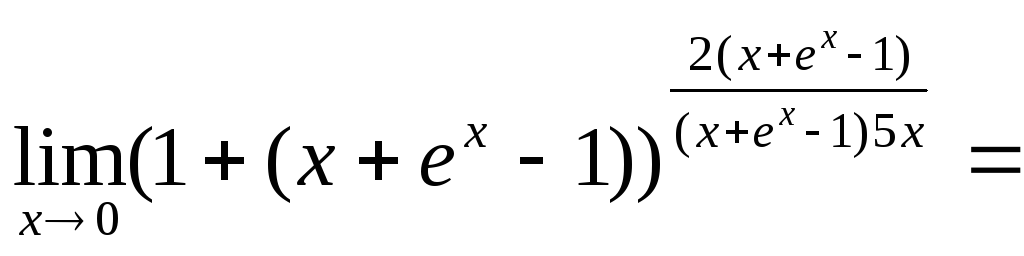
=
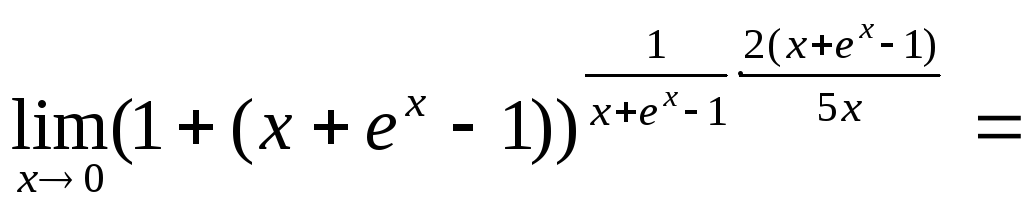
=![]() =
=
![]() .
.
3.
![]() ;
При
;
При
![]() получаем неопределенность
получаем неопределенность
![]() для раскрытия которой сначала упростим
выражение, а затем применим формулы
(7), (13), (15):
для раскрытия которой сначала упростим
выражение, а затем применим формулы
(7), (13), (15):
 =
=
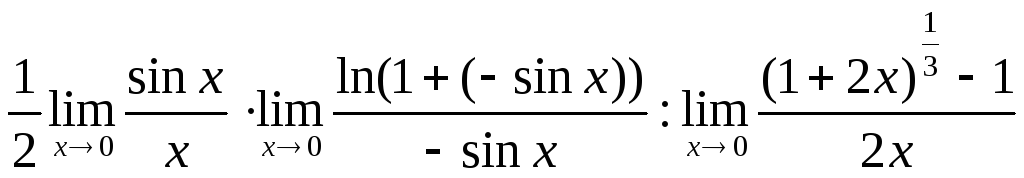 =
=
=
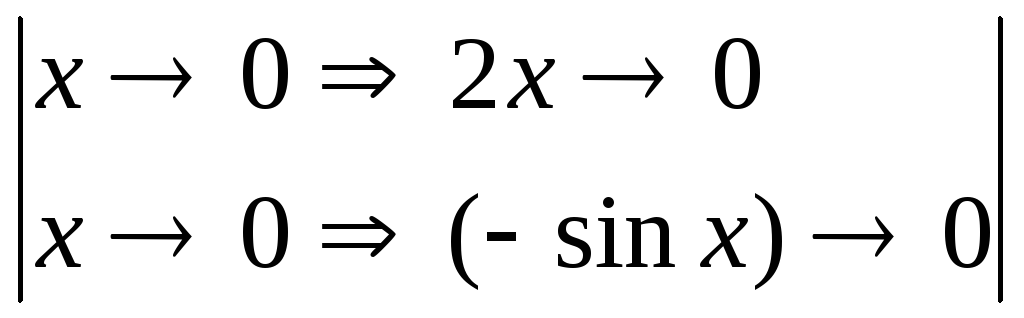 =
=
![]() .
.
4.
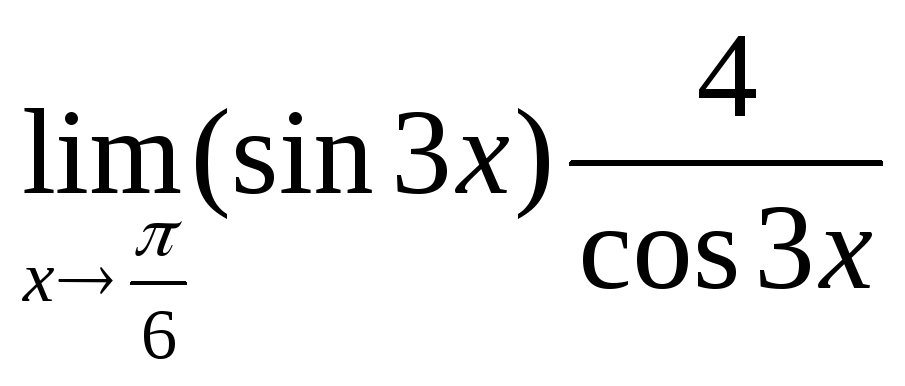 .Имеем
неопределенность вида
.Имеем
неопределенность вида
![]() .
Сделаем замену переменной. Пусть
.
Сделаем замену переменной. Пусть
![]() ,
тогда
,
тогда
![]() .
При
.
При
![]() новая переменная
новая переменная
![]() .
При этом
.
При этом
![]() ,
,
![]() ,
а
,
а
![]()
Подставив полученные выражения в формулу, получим
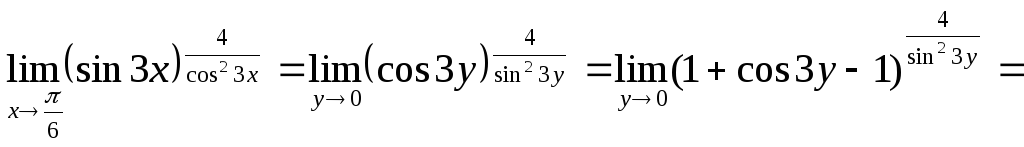
=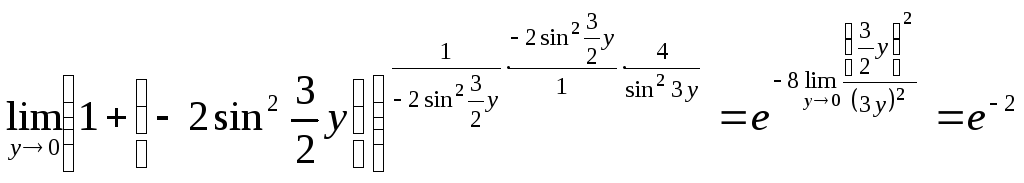
Эквивалентность функции
Пример 1. Вычислить предел функции в точке, заменяя бесконечно малые эквивалентными им:
.1)
![]() ;Непосредственное
вычисление предела приводит к
неопределенности типа
;Непосредственное
вычисление предела приводит к
неопределенности типа
![]() .
Используем формулу (16), а также формулы
(22), (24), (17) таблицы эквивалентных функций.
.
Используем формулу (16), а также формулы
(22), (24), (17) таблицы эквивалентных функций.
При этом
выполняются условия
![]() ,
,
![]() ,
если
,
если
![]() ,
которые являются обязательными для
перехода к эквивалентным функциям.
Тогда
,
которые являются обязательными для
перехода к эквивалентным функциям.
Тогда

Заметим, что решение примера с таким условием уже дано выше (см. 3-е условие примера 2 из параграфа 16.2).
2)
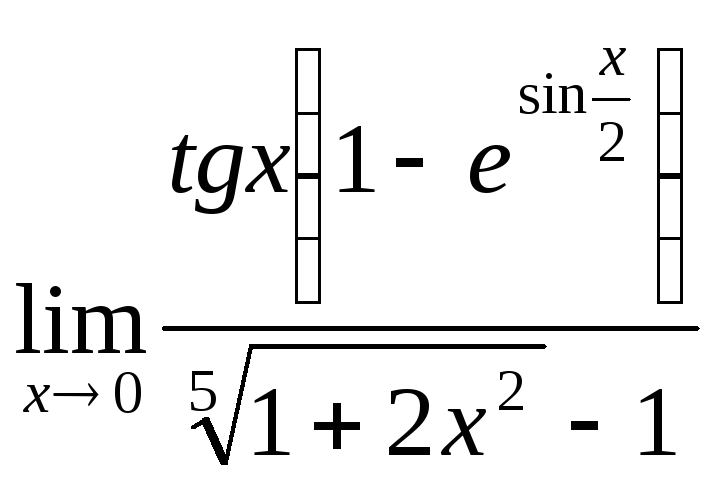 ;При
подстановке
;При
подстановке
![]() в выражения, получаем неопределенность
вида
в выражения, получаем неопределенность
вида
![]() .
Чтобы от нее избавится, воспользуемся
формулами (18), (23), (24) таблицы эквивалентных
бесконечно малых. Получим, что при
.
Чтобы от нее избавится, воспользуемся
формулами (18), (23), (24) таблицы эквивалентных
бесконечно малых. Получим, что при
![]() ,
,
![]() .
.
![]() .
.
![]()
Подставив полученные эквивалентные вместо соответствующих бесконечно малых, получим:
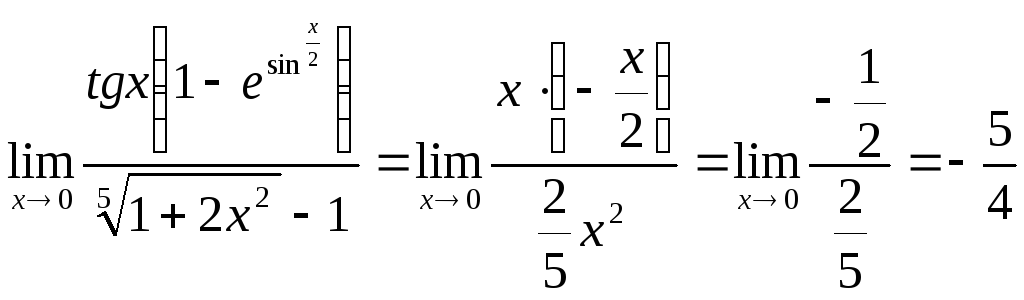
3. Преобразуем
выражение, стоящее под знаком предела
и используем формулу (19). 3)
![]() ;
;
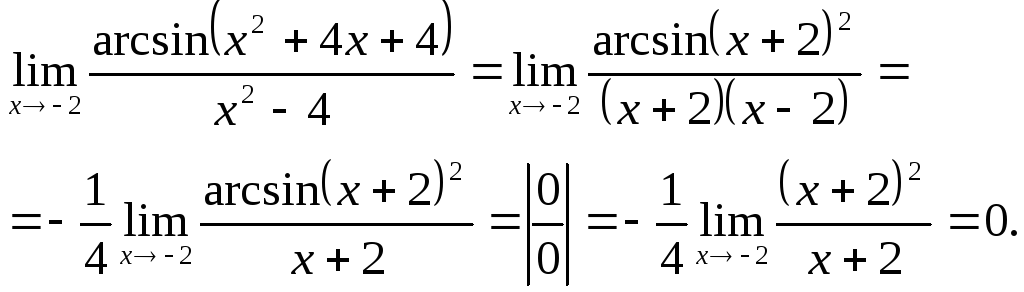
Использование
формулы (19) было обосновано тем, что
![]() если
если
![]() .
.
4)
![]() .
Замечаем, что непосредственное вычисление
предела приводит к неопределенности
.
Замечаем, что непосредственное вычисление
предела приводит к неопределенности
![]() .
Вместе с тем,
.
Вместе с тем,
![]() ,
если
,
если
![]() ,
а поэтому можем использовать формулу
(20). Тогда
,
а поэтому можем использовать формулу
(20). Тогда
![]() .
.
Пример 2.
Вычислить предел:
![]() .
.
Решение.
I
способ. При
![]() получим, что
получим, что
![]() и
и
![]()
Следовательно,
получим неопределенность вида
![]() .
Сделаем замену переменной. Введем такое
t,
чтобы
.
Сделаем замену переменной. Введем такое
t,
чтобы
![]() ,
если
,
если
![]() .
.
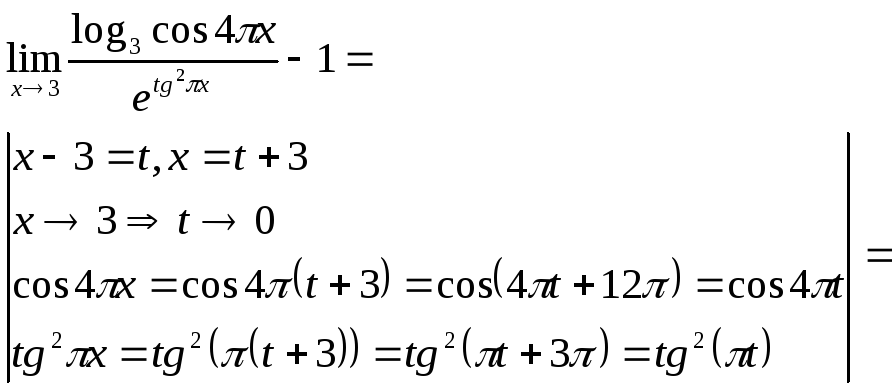
=![]() .
.
Дальше заменим бесконечно малые в числителе и знаменателе на эквивалентные по формулам (21), (23), (22), (18).
Мы имеем право
сделать это в преобразованных выражениях,
т.к. для соответствующей функции
![]() выполняется
выполняется
![]() ,
если
,
если
![]() .
Получаем:
.
Получаем:
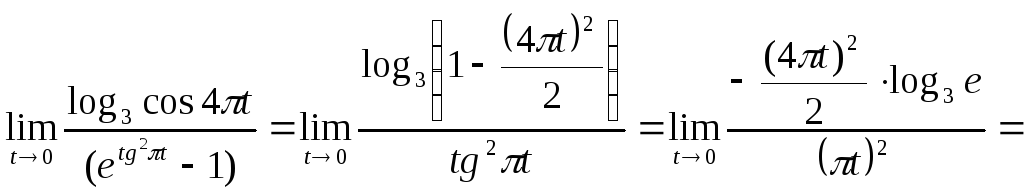
=
![]() .
.
II
способ. Поскольку
при непосредственном вычислении предела
имеем неопределенность типа
![]() ,
то необходимо преобразовать выражение,
стоящее под знаком предела. Однако сразу
использовать таблицу эквивалентности
бесконечно малых нельзя поскольку
,
то необходимо преобразовать выражение,
стоящее под знаком предела. Однако сразу
использовать таблицу эквивалентности
бесконечно малых нельзя поскольку
![]() ,
,
![]() ,
если
,
если
![]() .
Используем свойство периодичности
тригонометрических функций, получим
.
Используем свойство периодичности
тригонометрических функций, получим
![]() Выражение
под знаком предела преобразовано таким
образом, что
Выражение
под знаком предела преобразовано таким
образом, что
![]() и
и
![]() ,
если
,
если
![]() .
Поэтому можно использовать формулы
эквивалентности (21), (23), (22), (18). В результате
получаем
.
Поэтому можно использовать формулы
эквивалентности (21), (23), (22), (18). В результате
получаем