11.6. Понятие о кривизне кривой линии и о радиусе кривизны. Естественные оси

Криволинейное движение точки может быть определено или уравнениями движения в декартовых координатах, или траекторией и законом движения по этой траектории. В первом случае ускорение находится по его проекциям на координатные оси.

Во втором случае, ускорение находится по его проекциям на оси, направления которых связаны с данной траекторией, а именно: на касательную к траектории, главную нормаль и бинормаль. Но, прежде чем переходить к выводу формул для проекций ускорения на эти оси, необходимо рассмотреть некоторые геометрические понятия.

Пусть дана некоторая кривая (траектория точки), возьмем на ней две близкие точки А и В; длину дуги 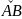обозначим через (рис.11.6). Проведем в точках А и В касательные к данной кривой (в направлении от А к В)

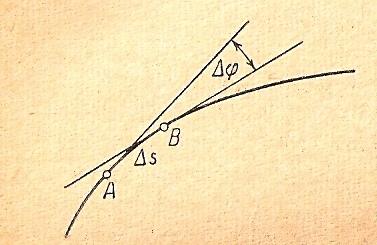Рис.11.6.

Угол между этими касательными называется углом смежности и измеряется в радианах, обозначим его 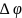. Отношение средней кривизной дуги . Будем теперь приближать точку В к точке А. Предел к которому стремится средняя кривизна дуги , когда точка В неограниченно приближается к точке А, называется кривизной данной линии в точке А. Если обозначим кривизну через к, то:

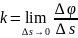
Величина, обратная кривизне, называется радиусом кривизны данной кривой в точке А. Обозначив радиус кривизны через ρ, получим:

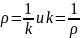
Для прямой линии кривизна равна нулю и, следовательно, радиус кривизны равен бесконечности. Окружность представляет собой кривую линию постоянной кривизны, равной обратной величине ее радиуса. Радиус кривизны окружности равен ее радиусу. Следовательно, радиус кривизны кривой линии есть радиус такой окружности, которая имеет с данной кривой в данной точке одинаковую кривизну.

Если траектория точки есть плоская кривая, заданная уравнением 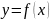, то радиус кривизны в какой-нибудь точке этой кривой можно вычислить по формуле:

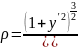
Где 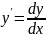, а абсолютное значение второй производной 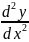в выбранной точке данной кривой.

В общем случае траектория движущейся точки М представляет собой кривую линию, не лежащую в одной плоскости, т.е. линию двоякой кривизны.

Положение точки М на траектории будем определять дуговой координатой s, отсчитываемой от произвольно выбранной на траектории неподвижной точки О.

Проведем через точку М касательную Мt к траектории и будем определять положительное направление этой касательной единичным вектором τ, направленным по касательной в сторону возрастания дуговой координаты s и равным по модулю 1 (рис.11.7). Этот вектор называется ортом касательной.

Рис.11.7.

Если проведем через точку М плоскость, перпендикулярную к касательной в этой точке, то такая плоскость называется нормальной плоскостью. Любая прямая, проведенная через точку М в нормальной плоскости, перпендикулярна к касательной Мt и является нормалью к траектории в точке М.

Необходимо найти в этом множестве нормалей главную нормаль. Для этого возьмем на траектории точку М', возле точки М.

Орт касательной в точке М' обозначим через τ' и проведем через точку М прямую Мt', параллельную вектору τ'. Построим плоскость, проходящую через две прямые Мt и Мt'. Будем точку М' неограниченно приближать к точке М так, чтобы в пределе эти точки совпали. Так как направление вектора τ' и прямой Мt' будет при этом изменяться, то будет меняться и положение плоскости tМt'. Эта плоскость будет поворачиваться относительно прямой Мt, приближаясь к предельному положению. Плоскость в предельном положении при М'→М называется соприкасающейся плоскостью данной кривой в точке М. Следовательно касательная в точке М лежит в соприкасающейся плоскости.

Нормаль, лежащая в соприкасающейся плоскости (линия пересечения нормальной и соприкасающейся плоскостей), называется главной нормалью данной кривой в точке М.

За положительное направление главной нормали принимается направление от точки М в сторону вогнутости траектории. Направление главной нормали будем определять единичным вектором n, направленным по главной нормали в положительную сторону (рис.11.8). Этот вектор n называется ортом главной нормали. Нормаль, перпендикулярная к соприкасающейся плоскости, называется бинормалью. Орт бинормали будем обозначать через b.

Рис.11.8.

Положительное направление орта бинормали будем определять так, чтобы три вектора τ, n и b были ориентированы по отношению друг к другу как орты i, j, k правой системы координат. Следовательно, орт b связан τ и n следующим соотношением

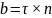
Три оси, имеющие начало в точке М и направленные по касательной, главной нормали и бинормали траектории в этой точке называются естественными осями и являются ребрами естественного триэдра (трехгранника).

Если отложить на главной нормали в положительном направлении отрезок МС=ρ, где ρ – радиус кривизны траектории в точке М и принять точку С за центр, можно провести в соприкасающейся плоскости окружность радиусом ρ. Эта окружность, имеющая в данной точке М общую касательную и общую кривизну с траекторией точки, называется соприкасающимся кругом или кругом кривизны. Центр С этой окружности называется центром кривизны данной кривой, соответствующим точке М.

11