54. Биномиальным дифференциалом называется выражение вида

, a,bR, m,n,p Q .

I. р – целое, р 0.

р<0, p-N, нужно делать замену переменной t= , где S=НОК(m,n).

II. p – дробное, но – целое. Пусть р =r/s, t=

III. p – дробное, – дробное, +р – целое,

p= r/s, t= = .

55. Определённый интеграл. Задачи, приводящие к понятию определённого интеграла. Определение определённого интеграла.

Задача о площади криволинейной трапеции: Рассмотрим плоскую фигуру ограниченную y=f(x), разобьём её точками a=x0<x1<…<xn=b, . В каждом из частичных сегментов выберем точку «кси итая».

. Обозначим через если существует конечный предел интегральной суммы при лямбда , то этот предел – площадь криволинейной трапеции.

Опр.: Пусть дана ф-я f(x) на [a,b]. Разобьём отрезок точками a=x0<x1<…<xn=b, . В каждом из частичных сегментов выберем точку «кси итая». Обозначим через . Если существует конечный предел , то он наз определённым интегралом от f(x).

56. Условия существования определённого интеграла. Свойства определённого интеграла.

Теор.: (необходимое условие существования определённого интеграла) для того чтобы существовал определённый интеграл необходимо чтобы ф-я была непрерывна на интервале интегрирования.

Док-во: (метод от противного) пусть ф-я интегрируемая но не ограниченная на [a,b]….

Теор.: (дост. условие существования определённого интеграла) Если ф-я непрерывна на [a,b], то она интегрируема на нем.

Свойства определенного интеграла.

1. 

2. 

3. 

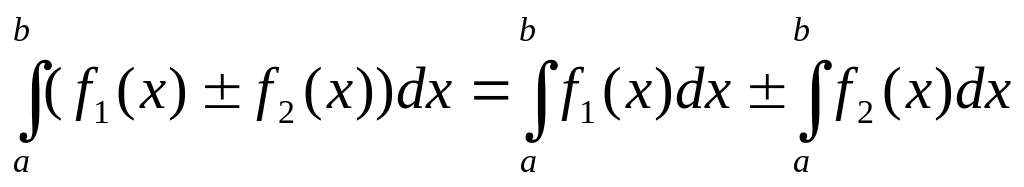
4. Если f(x)  (x) на отрезке [a, b] a < b, то

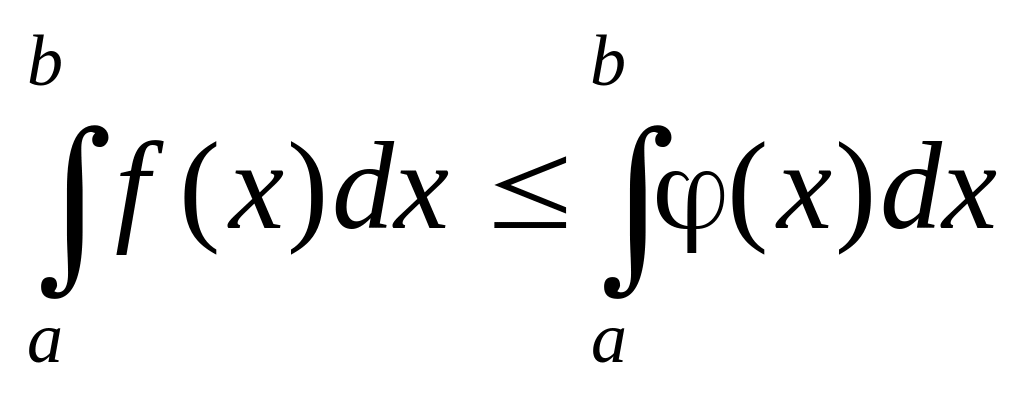
5. Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

6. Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка  такая, что

7) Для произвольных чисел a, b, c справедливо равенство:

8)

57. Вычисление определённого интеграла с помощью формулы Ньютона-Лейбница. Замена переменной и интегрирование по частям в определённом интеграле.

Теорема: (Теорема Ньютона – Лейбница)Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то .

Замена переменных.

Пусть задан интеграл , где f(x) – непрерывная функция на отрезке [a, b].

Введем новую переменную в соответствии с формулой x = (t).

Тогда если

1) () = а, () = b

2) (t) и (t) непрерывны на отрезке [, ]

3) f((t)) определена на отрезке [, ], то , тогда

Интегрирование по частям.

Если функции u = (x) и v = (x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

58. Вычисление площадей с помощью определённого интеграла. Вычисление площадей в параметрической форме.

Пусть кривая задана параметрически, тогда .

59. Вычисление площади фигуры в полярных координатах.

Пусть дан сектор АВО, ограниченный кривой АВ и двумя радиус векторами. >0 и непрерывная на . Разобьем сектор на n произвольных частей углами . Выберем в каждом сегменте точку «кси итая» r=r(«кси итая»). S=0.5*R²*l. Значит площадь сегмента = . Площадь всего сектора это сумма этих площадей. Тогда переходим к интегралу: .