
- •Учебно-методическое пособие для выполнения индивидуального задания определенный интеграл
- •Предисловие
- •Понятие определенного интеграла. Вычисление определенных интегралов
- •1. Понятие определенного интеграла
- •2. Условия интегрируемости функций
- •4. Свойства определенного интеграла
- •5. Вычисление определенного интеграла
- •1. Непосредственное интегрирование.
- •2. Интегрирование по частям определенного интеграла
- •3. Замена переменной в определенном интеграле
- •Решение задач I типового варианта
- •6. Вычисление несобственных интегралов
- •Решение задач II типового варианта
- •7. Приложение определенных интегралов к задачам геометрии
- •1. Вычисление площадей плоских фигур
- •2. Вычисление объемов тел вращения
- •3. Вычисление длин плоских кривых при различных способах задания линий основные понятия и формулы
- •Решение задачи III типового варианта
- •Решение задачи IV типового варианта
- •Знания и умения, которыми должен владеть студент
- •1. Знания на уровне понятий, определений, описаний, формулировок
- •Содержание
- •Учебно-методическое пособие для выполнения индивидуального задания определенный интеграл
2. Вычисление объемов тел вращения
Телом будем называть любое ограниченное множество точек пространства.
Тело вращения – тело, полученное в результате вращения фигуры вокруг некоторой оси (оси вращения).
Объем тела вращения – аддитивная величина, следовательно, объем тела вращения можно определить с помощью определенного интеграла.
Вычисление объема в прямоугольной системе координат. Воспользуемся дифференциальным методом.
Найти дифференциал объема
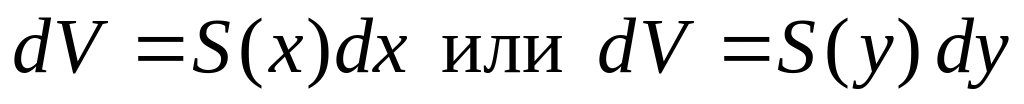 как главную часть приращения объема.
как главную часть приращения объема.Определить пределы интегрирования .
Вычислить объем
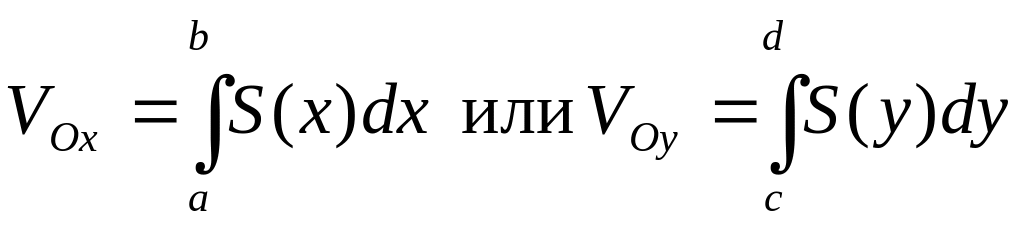 .
.
Дифференциал объема в прямоугольной системе координат – объем цилиндра с бесконечно малой высотой и переменным основанием.
Форма записи дифференциала объема зависит от условий задачи – от того, как задана фигура, которая в результате вращения образует тело, и что принято за ось вращения.
О сь
вращения будем отмечать дугой со стрелкой
сь
вращения будем отмечать дугой со стрелкой

2. y
1
![]()
 . y
. y





 y
y

 O
a x a=0 dx b x
O
a x a=0 dx b x
 dx
dx
![]()
![]() .
. ![]()
![]() .
.
 4.
y
4.
y
3
 .
y
.
y
![]()

d
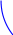


 d
d
![]()


 dy
dy

 dy
dy
 c
c

 O x c=0 x
O x c=0 x
![]()
![]() .
. ![]()
![]() .
.
Замечание. На всех чертежах изображено сечение тела плоскостью чертежа.
Задача
7.2.1. Фигура, ограниченная линиями
![]() ,
вращается вокруг оси
.
Найти объем тела вращения.
,
вращается вокруг оси
.
Найти объем тела вращения.
▲
![]() – полукубическая
парабола, смещенная на 1 вправо по оси
.
– полукубическая
парабола, смещенная на 1 вправо по оси
.
![]() – прямая.
– прямая.
Точки пересечения полукубической параболы и прямой:
![]()
 .
Построение очевидно.
.
Построение очевидно.
![]() y
y
 B
B
 O 1
2 x
O 1
2 x
dx
1) Имеем дифференциал
объема:
![]() .
.
2)
Пределы по чертежу:
![]() .
.
3)
Вычислим объем:
![]() .
▼
.
▼
Задача
7.2.2. Фигура, ограниченная линиями
![]() ,
вращается вокруг оси
,
вращается вокруг оси
![]() .
.
Найти объем тела вращения.
▲
![]() – парабола,
– парабола,
![]() – прямая. Точки пересечения параболы
и прямой:
– прямая. Точки пересечения параболы
и прямой:
![]() .
Построим чертеж:
.
Построим чертеж:
 y
y



![]()


 A
A
![]()
![]()

O 4 x
1) Найдем
![]() .
.
2)
Пределы определяем из решения системы
при определении точек пересечения
параболы и прямой:
![]() .
.
3) Вычисляем объем:
![]() .
▼
.
▼
Вычисление объема при параметрическом задании линий, ограничивающих фигуру.
Задача
7.2.3. Фигура, ограниченная одной
аркой циклоиды
![]() и осью
вращается вокруг оси
.
Найти объем тела вращения.
и осью
вращается вокруг оси
.
Найти объем тела вращения.
▲ Чертеж циклоиды очевиден.


y

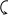
 O
dx 2πa
x
O
dx 2πa
x
1)
![]() .
.
2) Пределы определяются
по пределам
![]() из зависимости
из зависимости
![]() .
Имеем
.
Имеем
|
0 |
|
|
0 |
|
3)
![]()
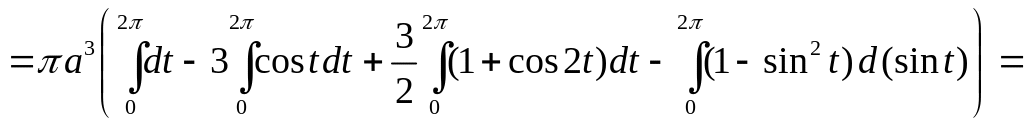
![]() .
.
3. Вычисление длин плоских кривых при различных способах задания линий основные понятия и формулы
1. Длина кривой.
Рассмотрим на плоскости кривую , заданную параметрически:
![]() ,
,
где
![]() – непрерывные функции на отрезке
,
причем различным значениям
– непрерывные функции на отрезке
,
причем различным значениям
![]() соответствуют различные точки
соответствуют различные точки
![]() (т. е. нет кратных точек). Такую кривую
назовем простой
(плоской)
незамкнутой кривой.
(т. е. нет кратных точек). Такую кривую
назовем простой
(плоской)
незамкнутой кривой.
Если точки
![]() совпадают, а остальные точки не являются
кратными, то кривая
называется простой
замкнутой кривой.
совпадают, а остальные точки не являются
кратными, то кривая
называется простой
замкнутой кривой.
Длина дуги – аддитивная величина, следовательно, ее можно найти с помощью определенного интеграла.
Воспользуемся дифференциальным методом.
Найти дифференциал дуги
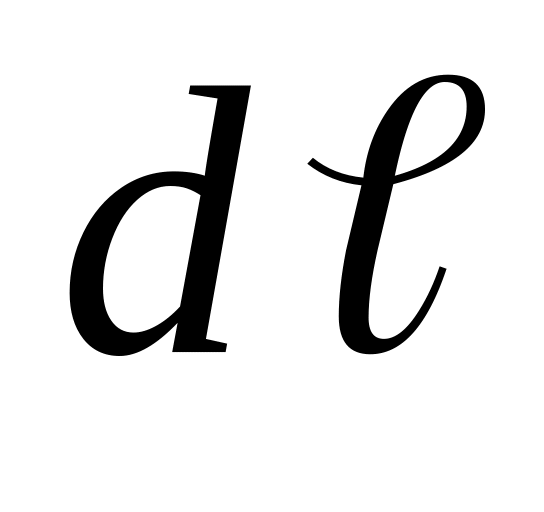 в зависимости от способа задания кривой.
в зависимости от способа задания кривой.Определить пределы интегрирования.
Вычислить интеграл от дифференциала дуги.
2. Длина кривой в декартовых координатах. Если кривая задана уравнением
![]() ,
,
причем функция имеет на отрезке непрерывную производную, то дифференциал дуги вычисляется по формуле
![]() ,
,
а длина кривой по формуле
![]() .
.
Если кривая задана уравнением
![]() ,
,
причем функция
![]() имеет на отрезке
имеет на отрезке
![]() непрерывную производную, то дифференциал
дуги вычисляется по формуле
непрерывную производную, то дифференциал
дуги вычисляется по формуле
![]() ,
,
а длина кривой по формуле
![]() .
.
3. Длина кривой,
заданной параметрически. Пусть кривая
задана параметрическими уравнениями
![]() ,
причем функции
,
причем функции
![]() имеют на отрезке
непрерывные производные. Тогда
дифференциал дуги выражается формулой
имеют на отрезке
непрерывные производные. Тогда
дифференциал дуги выражается формулой
![]()
а длина кривой
![]() .
.
4. Длина кривой в
полярных координатах. Если кривая
задана уравнением
,
![]() ,
причем функция
,
причем функция
![]() имеет на отрезке
непрерывную производную, дифференциал
дуги выражается формулой
имеет на отрезке
непрерывную производную, дифференциал
дуги выражается формулой
![]() ,
,
а длина кривой
![]() .
.
Замечание. Задачи на вычисление длин дуг можно решать без чертежа.
Задача
7.3.1. Найти длину дуги кривой
![]() .
.
▲
1.
![]()
![]() .
.
2.
Пределы заданы в условии задачи
![]() .
.
3.

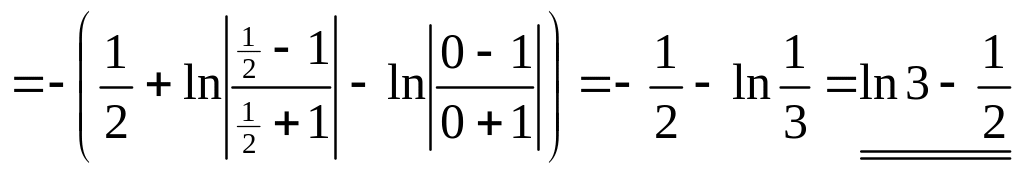 .
▼
.
▼
Задача 7.3.2. Вычислить длину дуги одной арки циклоиды .
▲ Кривая задана параметрически.
1.
![]()
![]() .
.
2.
Пределы для переменной
определяются по пределам
![]() из уравнения
из уравнения
|
0 |
|
|
0 |
|
3.
![]() .
▼
.
▼
Задача
7.3.3. Вычислить длину логарифмической
спирали
![]() .
.
▲ Кривая задана в полярной системе координат.
1.
![]() .
.
2.
Пределы заданы по условию задачи:
![]() .
.
3.
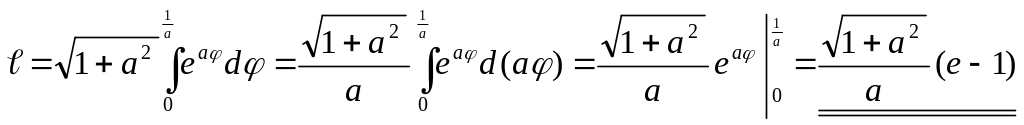 .
.
