1.5 Решение задачи линейного программирования

		15	15	15	15	20
	Vj Ui	V1=30	V2=8	V3=11	V4=12	V5=26
21	U1=0	30 6	24 8	11 15	12 0	25 26
19	U2=4	26 4	4 15	29 7	20 8	24 20
15	U2=2	27 28	14 6	14 9	10 15	18 24
25	U2=24	6 5	14 16	28 13	8 -12	2 20

F=6*30+15*11+4*26+15*4+15*10+5*6+20*2=729

		15	15	15	15	20
	Vj Ui	V1=12	V2=12	V3=11	V4=12	V5=20
21	U1=0	30 12	24 12	11 15	12 6	25 20
19	U2=8	26 4	4 15	29 3	20 4	24 12
15	U2=2	27 10	14 10	14 9	10 9	18 6
25	U2=6	6 11	14 6	28 5	8 6	2 14

F=15*11+6*12+4*26+15*4+9*10+6*18+11*6+14*2=693 (ед)

2 Графы и их применение

1. Основные понятия теории графов

Графы формально описывают множество близких ситуаций. Самым привычным примером служит карта автодорог, на которой изображены перекрестки и связывающие их дороги. Перекрестки являются вершинами графа, а дороги - его ребрами. Иногда наши графы ориентированы (подобно улицам с односторонним движением) или взвешены - каждой дороге приписана стоимость путешествия по ней (если, например, дороги платные). Когда мы изучим язык графов подробнее, аналогия с картой автодорог станет еще более глубокой.

Иногда приходится распространять ту или иную информацию среди большой группы людей или по всем компьютерам большой сети. Мы хотели бы, чтобы информация достигла каждого участника группы, но при этом ровно по одному разу. В некоторых группах для этой цели организуется "телефонное дерево", когда каждый из членов группы, получив свежую новость, сообщает ее небольшому числу других участников. Если каждый из членов группы встречается в дереве лишь однажды, а высота дерева не очень велика, то информация очень быстро доходит до всех. Для графов общего вида ситуация оказывается сложнее: в среднем графе гораздо больше связей, чем в дереве. Остовное дерево представляет собой связное подмножество графа, не содержащее циклов, включающее в себя все вершины графа и некоторые из его ребер. Минимальное остовное дерево это остовное дерево, имеющее минимально возможную сумму весов ребер.

Аналогичные приложения имеет и задача поиска кратчайшего пути в графе: умение решать такую задачу помогает планировать путь на автомобиле или посылать сообщение по компьютерной сети.

С формальной точки зрения граф представляет собой упорядоченную пару G = (V, Е) множеств, первое из которых состоит из вершин, или узлов, графа, а второе - из его ребер. Ребро связывает между собой две вершины. При работе с графами нас часто интересует, как проложить путь из ребер от одной вершины графа к другой. Поэтому мы будем говорить о движении по ребру; это означает, что мы переходим из вершины А графа в другую вершину В, связанную с ней ребром АВ (ребро графа, связывающее две вершины, для краткости обозначается этой парой вершин). В этом случае мы говорим, что А примыкает к В, или что эти две вершины соседние. Граф может быть ориентированным или нет. Ребра неориентированного графа, чаще всего называемого просто графом, можно проходить в обоих направлениях. В этом случае ребро - это неупорядоченная пара вершин, его концов. В ориентированном графе, или орграфе, ребра представляют собой упорядоченные пары вершин: первая вершина - это начало ребра, а вторая - его конец. Далее мы для краткости будем говорить просто о ребрах, а ориентированы они или нет будет понятно из контекста

На рисунке 1 изображено графическое представление неориентированного (а) и ориентированного (б) графов вместе с их формальным описанием.

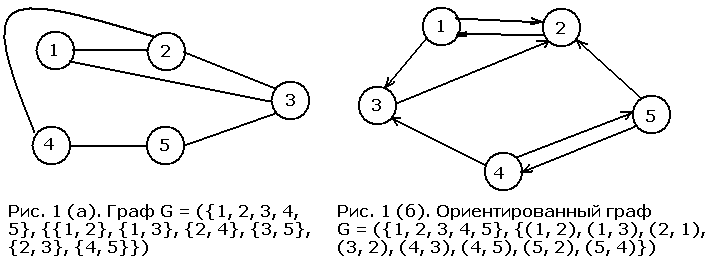
Полный граф - это граф, в котором каждая вершина соединена со всеми остальными. Число ребер в полном графе без петель с N вершинами равно (N² - N)/2. В полном ориентированном графе разрешается переход из любой вершины в любую другую. Поскольку в графе переход по ребру разрешается в обоих направлениях, а переход по ребру в орграфе - только в одном, в полном орграфе в два раза больше ребер, то есть их число равно N² - N.

Подграф (V_S, E_S) графа или орграфа (V, E) состоит из некоторого подмножества вершин и некоторого подмножества ребер, их соединяющих.

Путь в графе или орграфе - это последовательность ребер, по которым можно поочередно проходить. Другими словами, путь из вершины A в вершину B начинается в A и проходит по набору ребер до тех пор, пока не будет достигнута вершина B. С формальной точки зрения, путь из вершины v_i в вершину v_j это последовательность ребер графа v_iv_i+1, v_i+1v_i+2, ..., v_j-1v_j. Мы требуем, чтобы любая вершина встречалась на таком пути не более, чем однажды. У всякого пути есть длина - число ребер в нем. Длина пути AB, BC, CD, DE равна 4.

Во взвешенном графе или орграфе каждому ребру приписано число, называемое весом ребра. При изображении графа обычно записывают вес ребра рядом с ребром. При формальном описании вес будет дополнительным элементом неупорядоченной или упорядоченной пары вершин (образуя вместе с этой парой "триплет"). При работе с ориентированными графами мы считаем вес ребра ценой прохода по нему. Стоимость пути по взвешенному графу равна сумме весов ребер пути. Кратчайший путь во взвешенном графе - это путь с минимальным весом, даже если число ребер в пути и можно уменьшить. Если, например, путь P₁ состоит из пяти ребер с общим весом 24, а путь P₂ - из трех ребер с общим весом 36, то путь P₁ считается более коротким.

Граф или орграф называется связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл - это путь, который начинается и кончается в одной и той же вершине. В ациклическом графе или орграфе циклы отсутствуют. Связный ациклический граф называется (неукорененным) деревом. Структура неукорененного дерева такая же, что и у дерева, только в нем не выделен корень. Однако каждая вершина неукорененного дерева может служить его корнем.

Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.

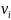
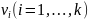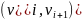Ориентированным путём в орграфе называют конечную последовательность вершин , для которой все пары , (i=1,…k-1) являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.

Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:

Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины.

Всякий простой неэлементарный путь содержит элементарный цикл.

Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).

Петля — элементарный цикл.