
- •1 Линейное программирование
- •1.1 Постановка задачи линейного программирования.
- •1.2. Формы записи задачи линейного программирования
- •Стандартная задача линейного программирования
- •Каноническая задача линейного программирования
- •Общая задача линейного программирования
- •1.3 Модель транспортной задачи
- •1.5 Решение задачи линейного программирования
- •2 Графы и их применение
- •Основные понятия теории графов
- •2.2 Сетевой график
- •2.3. Правила расчета основных параметров сетевого графика
- •2.4 Оптимизация сетевого графика
- •2.5 Рассчитать параметры сетевого графика
- •3 Игровые модели
- •Основные понятия теории игр
- •Классификация игр
- •Критерий Лапласа
- •Критерий Сэвиджа
- •Критерий Гурвица
Общая задача линейного программирования
В этой задачи часть ограничений носит характер неравенств, а часть является уравнениями. Кроме того, не на все переменные наложено условие неотрицательности:
max(

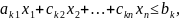
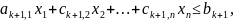
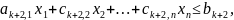
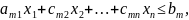
…,
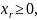 (9)
(9)
Здесь ![]() .
Ясно, что стандартная задача получается
как частный случай общей при
.
Ясно, что стандартная задача получается
как частный случай общей при ![]() ;
каноническая — при
;
каноническая — при ![]() .
.
Все три перечисленные задачи эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных.
При
изучении задач линейного программирования
сложилась определенная терминология.
Линейная форма ![]() ,
подлежащая максимизации (или минимизации)
, называется целевой функцией. Вектор
,
подлежащая максимизации (или минимизации)
, называется целевой функцией. Вектор ![]() ,
удовлетворяющий всем ограничениям
задачи линейного программирования,
называется допустимым вектором, или
планом. Задача линейного программирования,
для которой существуют допустимые
векторы, называется допустимой задачей.
Допустимый вектор
,
удовлетворяющий всем ограничениям
задачи линейного программирования,
называется допустимым вектором, или
планом. Задача линейного программирования,
для которой существуют допустимые
векторы, называется допустимой задачей.
Допустимый вектор ![]() ,
доставляющий наибольшее значение
целевой функции по сравнению с любым
другим допустимым вектором
,
доставляющий наибольшее значение
целевой функции по сравнению с любым
другим допустимым вектором ![]() ,
т.е.
,
т.е. ![]() ,
называется решением задачи, или
оптимальным планом. Максимальное
значение
,
называется решением задачи, или
оптимальным планом. Максимальное
значение ![]() целевой
функции называется значением задачи.
целевой
функции называется значением задачи.
1.3 Модель транспортной задачи
Общая
постановка транспортной
задачи состоит
в определении оптимального плана
перевозок некоторого однородного груза
из т
пунктов отправления
![]() в
п
пунктов назначения
в
п
пунктов назначения
![]() .
При этом в качестве критерия оптимальности
обычно берется либо минимальная стоимость
перевозок всего груза, либо минимальное
время его доставки. Рассмотрим транспортную
задачу, в качестве критерия оптимальности
которой взята минимальная стоимость
перевозок всего груза. Обозначим через
.
При этом в качестве критерия оптимальности
обычно берется либо минимальная стоимость
перевозок всего груза, либо минимальное
время его доставки. Рассмотрим транспортную
задачу, в качестве критерия оптимальности
которой взята минимальная стоимость
перевозок всего груза. Обозначим через
![]() тарифы
перевозки единицы груза из i-го
пункта отправления в j-й
пункт назначения, через
тарифы
перевозки единицы груза из i-го
пункта отправления в j-й
пункт назначения, через
![]() –
запасы груза в i-м
пункте отправления, через
–
запасы груза в i-м
пункте отправления, через
![]() –
потребности в грузе в j–м
пункте назначения, а через
–
потребности в грузе в j–м
пункте назначения, а через
![]() –
количество единиц груза, перевозимого
из i-го
пункта отправления в j-й
пункт назначения. Тогда математическая
постановка задачи состоит в определении
минимального значения функции
–
количество единиц груза, перевозимого
из i-го
пункта отправления в j-й
пункт назначения. Тогда математическая
постановка задачи состоит в определении
минимального значения функции
![]() (10)
(10)
при условиях
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
Поскольку
переменные
![]() удовлетворяют
системам линейных уравнений (11) и (12) и
условию неотрицательности (13),
обеспечиваются доставка необходимого
количества груза в каждый из пунктов
назначения, вывоз имеющегося груза из
всех пунктов отправления, а также
исключаются обратные перевозки.
удовлетворяют
системам линейных уравнений (11) и (12) и
условию неотрицательности (13),
обеспечиваются доставка необходимого
количества груза в каждый из пунктов
назначения, вывоз имеющегося груза из
всех пунктов отправления, а также
исключаются обратные перевозки.
1.4 Двойственные задачи линейного программирования Каждой задаче линейного программирования можно поставить в соответствие задачу, называемую двойственной к исходной. Предположим, что в производстве используется m различных видов ресурсов, объем которых ограничен величинами b1, b2,.., bm. И производится n различных видов продукции, величина выпуска которых определяется переменными х1, х2,…, хn. Известны нормы затрат каждого ресурса на единицу каждого вида продукции, образующие матрицу
Известна также стоимостная оценка (цена) единицы продукции каждого вида с1, с2,…, сn. Задача сводится к следующему: найти такие значения переменных х1, х2,…, хn, при которых расход ресурсов не превышает заданного их количества, а стоимость всей продукции достигает максимума. В математической форме задача записывается следующим образом: максимизировать L = c1x1+c2x2+…+cnxn (15) при условия
На базе тех же исходных данных может быть поставлена еще одна задача, в которой переменными величинами являются оценки у1,у2,…,уm, приписываемые каждому виду ресурсов. Они должны быть такими, чтобы общая оценка всего имеющегося количества ресурсов была минимальной, но при условии, что суммарная оценка ресурсов, расходуемых на единицу любого вида продукции, будет не меньше, чем цена за эту единицу. Математическая задача записывается следующим образом: минимизировать L = b1y1+b2y2+…+bmym (17)
при
условиях |
Двойственная задача линейного программирования
1. Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу, называемую двойственной или сопряженной по отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции
F=c1x1+c2x2+…+CnXn (19)
При условиях
A11x1+a12x2+…+A1nXn≤b1,
A21x1+a22x2+…+A2nXn≤b2,
……………………………….
Ar1X1+Ar2X2+…+ArnXn≤br,
Ar+11X1+Ar+12X2+…Ar+1nXn=br+1, (20)
………………………………………….
Am1x1+am2x2+…+mnXn=bm,
Xj≥0 (J=1,l≤n). (21)
Определение 1.14. Задача, состоящая в нахождении минимального значения функции
F*=b1y1+b2y2+…bmyYm (4)
При условиях
A11y11+a21y2+…+am1ym≥c1,
A12y1+a22y2+…+am2ym≥c2
……………………………….. (22)
A1nY1+a2ny2+…+AmnYm=Cm,
Yj≥0 (l=1,r,r≤m), (23)
Называется двойственная по отношению к задаче
Задачи 19-20 и 21-22 образуют пару задач, называемую в линейном программировании двойственной парой.
Сравнивая две сформулированные задача по отношению к исходной составляется согласно следущим правилам:
Целевая функция исходной задачи 19-20 задается ее максимум, а целевая функция двойственной 22-23 на минимум.
Матрица
 (24)
(24)
Составленная из коэффициентов при неизвестных в системе ограничений(20) исходной задачи 19-20, и аналогичная матрица
 (25)
(25)
В двойственной задаче 22-24 получают друг из друга транспортированием
3. Число переменных в двойственной задаче (22-24) равно числу соотношений в системе (2) исходной задачи (19)-(21), а число ограничений в системе(23) двойственной задачи----числу переменных в исходной задаче.
4.Коэффициентами при неизвестных в целевой функции(22) двойственной задачи (22)-(24) являются свободные члены в системе(20) исходной задачи (19)-(21), а правым частям в соотношениях системы(23) двойственной задачи---коэффициенты при неизвестных в целевой функции (19) исходной задачи.
5. Если переменная Xj исходной задачи (19)-(20) может принимать только лишь положительные значения то J-e условие в системе(23) двойственной задачи(22)-(24) является неравенством вида “≥”. Если же переменная Xj может принимать как положительные так и отрицательные значения, то j-e соотношение в системе(23) представляет собой уравнение. Аналогичные связи имеют место между ограничениями(2) исходной задачи(19)-(21) и переменными двойственной задачи (22)-(24). Если j-e соотношение в системе (20) исходной задачи является неравенством, то l-я переменная yl может принимать как положительные, так и отрицательные значения.

 (14)
(14)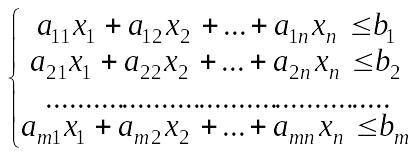 (16)
(16)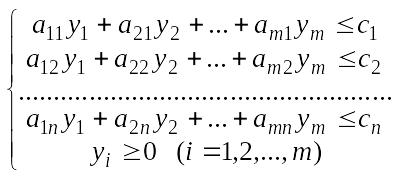 (18)
(18)