Задачи для самостоятельного решения.

Решить игру 2х2:

1. 2. 3. 4.

5. 6. 7. 8.

9. 10. 11. 12.

13. 14. 15. 16.

17. 18. 19. 20.

Принцип доминирования

Матрицы размерностью 2х2 встречаются не так часто, как нам того бы хотелось, поэтому рассмотрим принцип, позволяющий уменьшить размерность матрицы.

Первый игрок стремиться максимизировать свой выигрыш и ему будет выгодна та стратегия, которая принесет больший выигрыш. Если элементы некоторой строки платежной матрицы С меньше соответствующих элементов другой строки, то интуитивно ясно, первую можно вычеркнуть. Сформулируем условия доминирования строк и столбцов платежной матрицы, позволяющие уменьшить ее размерность.

Определение. Вектор доминирует вектор , если все элементы вектора x больше или равны соответствующим элементам вектора y. То есть , и хотя бы одно неравенство выполняется как строгое. Про вектор y говорят, что он доминируется вектором x.

Определение. Линейная комбинация векторов называется выпуклой, если существуют такие коэффициенты , не равные нулю одновременно, что выполнено условие

Теорема (о доминировании строк). Если в игре с платежной матрицей С какая-либо строка доминируется выпуклой комбинацией остальных строк, то она будет входить с нулевой вероятностью в оптимальную смешанную стратегию первого игрока и ее можно вычеркнуть.

Замечания к теореме:

1. Если в матрице существуют несколько одинаковых срок, то все, кроме одной можно вычеркнуть, и они будут входить с нулевой вероятностью в оптимальную смешанную стратегию первого игрока.

2. Если какая-либо строка доминируется другой, то меньшую можно вычеркнуть.

Теорема (о доминировании столбцов). Если в игре с платежной матрицей C какой-либо столбец доминирует выпуклую комбинацию остальных столбцов, то он будет входить с нулевой вероятностью в оптимальную смешанную стратегию второго игрока и его можно вычеркнуть.

Пример Используя принцип доминирования найти оптимальную стратегию.

Решение. Третий и четвертый столбец доминируют над вторым, поэтому, в соответствии с утверждением о доминировании строк, их можно вычеркнуть и они будут входить с нулевой вероятностью в оптимальную смешанную стратегию второго игрока.

Из оставшихся трех строк и двух столбцов, можно вычеркнуть первую строку, так как она доминируется третьей строкой. Оставшуюся игру 2х2 просто решить. Таким образом, оптимальными смешанными стратегиями игроков будут: , , .

Задачи для самостоятельного решения.

Используя принцип доминировании, решить игру:

1. 2. 3.

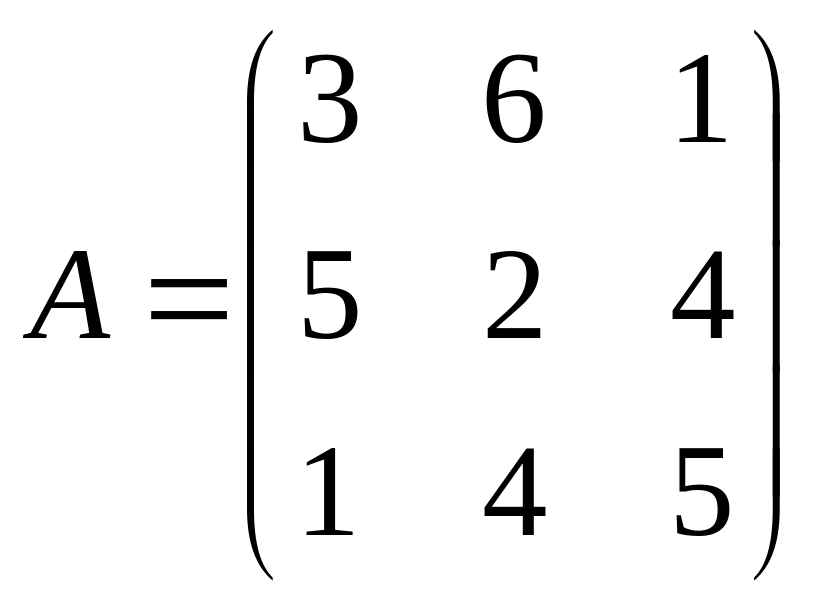
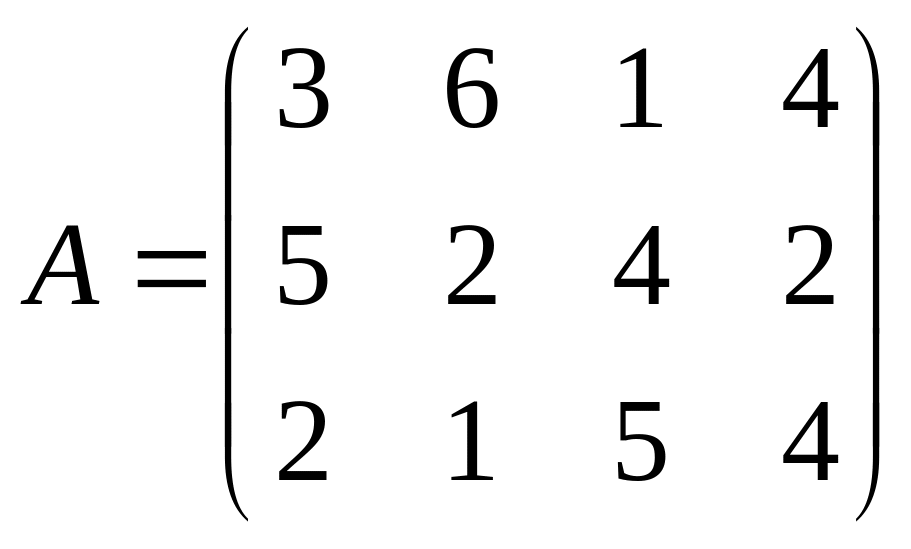
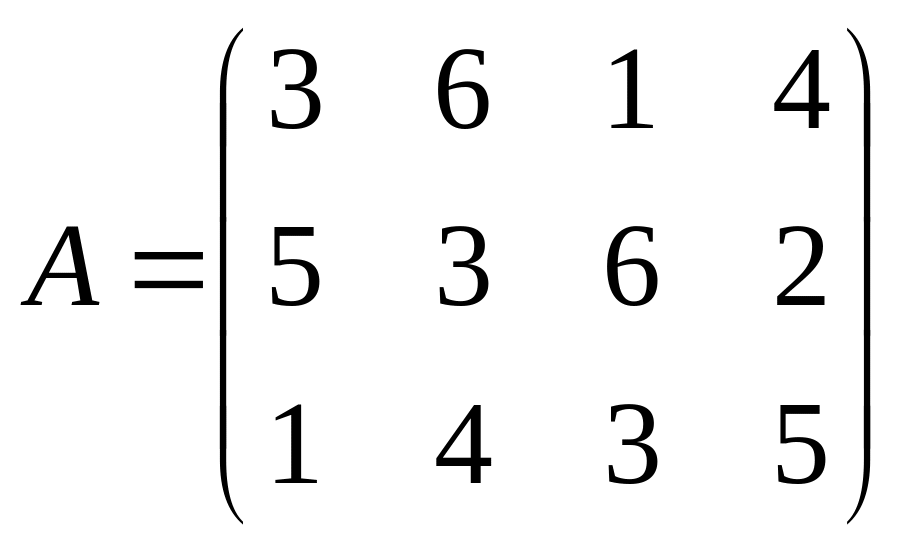
4. 5. 6.

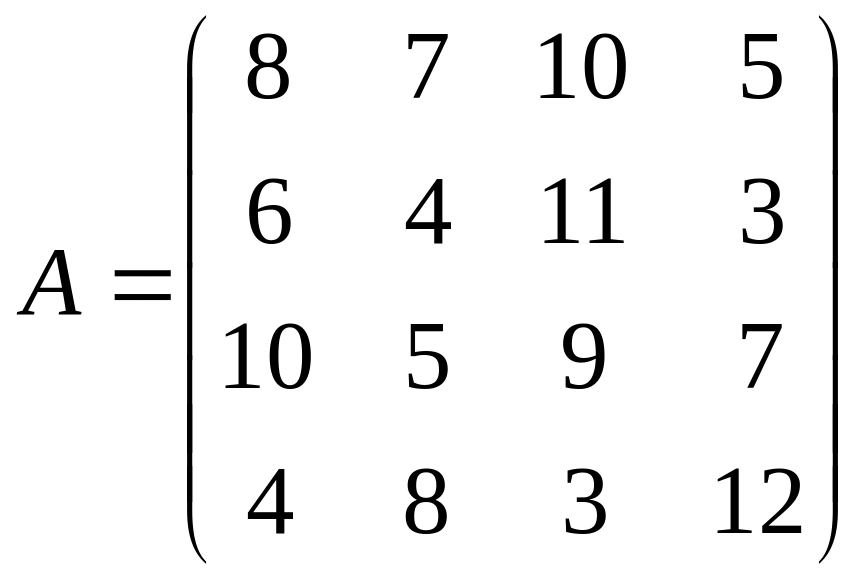
7. 8. 9.

10. 11. 12.

Графическое решение игр 2xm или nx2.

Рассмотрим сначала игру, в которой у первого игрока две стратегии, а у второго m стратегий. Тогда платежная матрица будет иметь вид:

Вектор смешанной стратегии первого игрока состоит из двух элементов, а второго – из m элементов, то есть и . Воспользуемся правой частью определения решения игры в смешанных стратегиях. Пусть первый игрок применил свою оптимальную смешанную стратегию, а второй любую, кроме оптимальной (поочередно свои чистые стратегии). Тогда, умножив вектор p на первый столбец матрицы, воспользуемся нормировочным условием, для того, чтобы сделать замену и получим функцию, зависящую от одной переменной:

.

Аналогично поступим со всеми остальными столбцами:

и т.д.

Последняя функция привет вид:

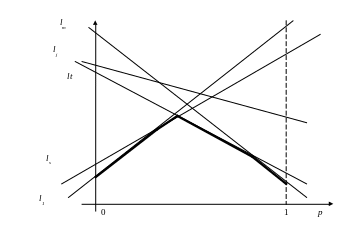
Сначала на плоскости последовательно рисуются прямые. Затем для каждого значения , путем визуального сравнения соответствующих ему значений l на каждой из построенных прямых определяется и отмечается минимальное из них. В результате описания процедуры получается ломаная, которая является нижней огибающей. Верхняя точка нижней огибающей определяет и цену игры и оптимальную стратегию.

Объясняется этот выбор просто. Оптимальной стратегией первого игрока является максиминная стратегия и поэтому из всех минимумов он выбирает максимум. Пересечение прямых, дающих точку максимума определяет выигрыш игрока, а номера прямых, которые пересекаются в этой точке соответствуют применению вторым игроком данных стратегий с вероятностью, отличной от нуля. Вероятности применений стратегий второго игрока, которые не участвуют в образовании точки экстремума, равны нулю.

В нашем случае эту точку дают пересечения прямых и . Разность между элементами одного столбца является угловым коэффициентом прямой и обозначим его через k. Тогда:

,

или через угловые коэффициенты

,

откуда просто определяется вероятность применения первым игроком своей первой стратегии: .

Для того чтобы определить выигрыш, достаточно подставить вероятность в любое равенство, дающее точку экстремума.

Остается определить вероятности применения стратегий вторым игроком. Для этого можно воспользоваться решением игры 2х2, а можно уже найденными угловыми коэффициентами прямых. Рассмотрим игру, составленную из строк и столбцов, вероятности применения которых игроками не равны нулю: .

Тогда для определений оптимальной стратегии второго игрока необходимо воспользоваться системой: 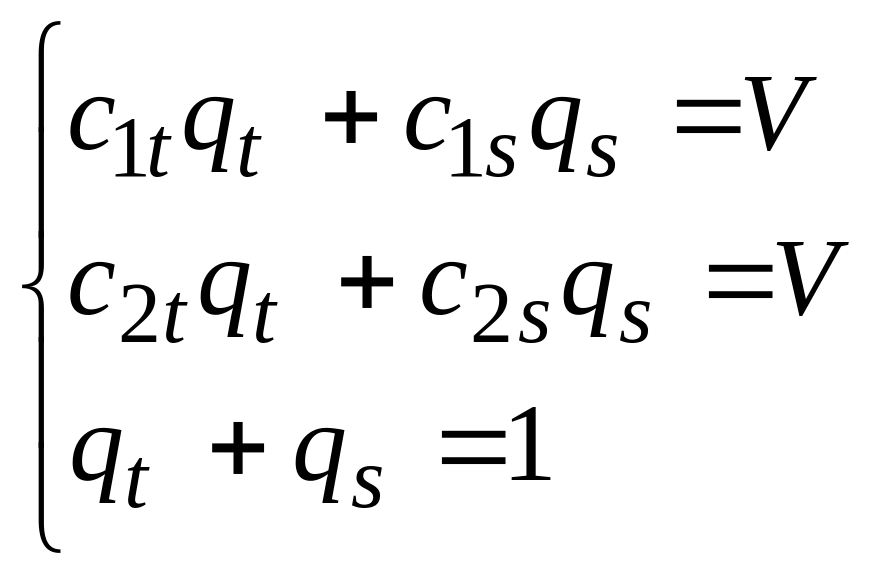. Вычтем из первого равенство второе и сделаем замену переменных и получим: , или в угловых коэффициентах . Откуда с помощью элементарных вычислений имеем: , и тогда будут являться оптимальными смешанными стратегиями второго игрока.

Пример. Рассмотрим игру, заданную матрицей .

.

Шаг 1. Проверим, имеет ли данная игра решение в чистых стратегиях. Нижняя цена игры равна 1, а верхняя – 4. Седловой точки нет. Следовательно, обязано существовать решение в смешанных стратегиях.

Составим функции для построения графика:

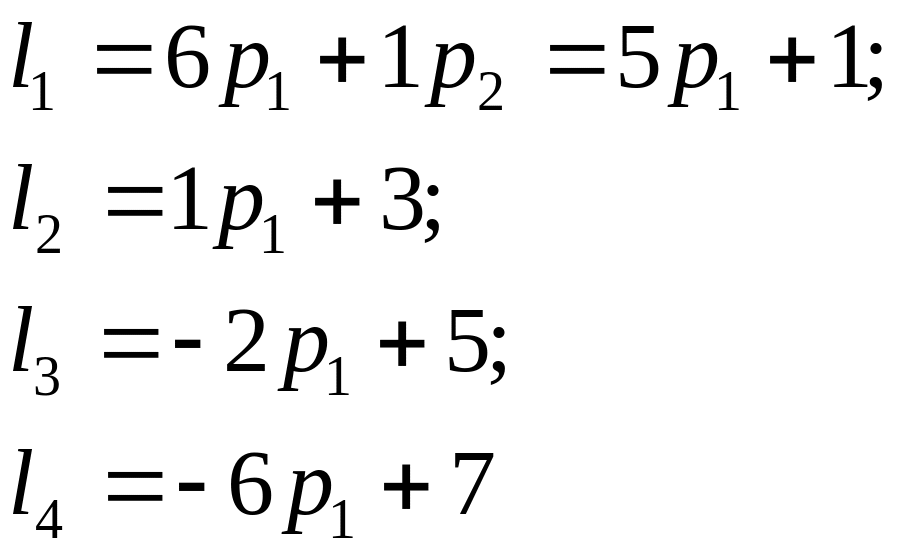
Построим график, где по оси абцисс отложим вероятность , а по оси ординат – выигрыш.

Нас интересует нижняя огибающая и максимальная точка из нее. Это пересечение первой и четвертой прямых. Тогда

, и, следовательно

Таким образом, оптимальная смешанная стратегия найдена. Найдем теперь оптимальные смешанные стратегии второго игрока. Так как в точке экстремума активными стратегиями являются первая и четвертая, то уравнение для нахождения оптимальных вероятностей второго игрока имеет вид: