
- •Вопрос №17 Понятие об алгоритмическом языке. Логические языки. Языки низкого и высокого уровня. Компилируемые и интерпретируемые языки. Функциональные языки.
- •Вопрос №18 Понятие алгоритма, основные свойства, способы записи алгоритма.
- •Вопрос №19 Структурные части алгоритма. Линейная часть, разветвление и цикл.
- •Линейные алгоритмы
- •Вопрос №20 Стандартные алгоритмы. Действия с целыми числами. Суммирование и умножение. Вычисление многочлена по схеме Горнера.
- •Вопрос № 21 Булева алгебра. Переменная логического типа. Операции с логической переменной. Логические выражения и логические операции
- •Логические переменные.
Вопрос №19 Структурные части алгоритма. Линейная часть, разветвление и цикл.
Основными алгоритмическими структурами являются - следование, ветвление(развилка) и цикл
Ниже приведены графические обозначения на блок-схемах.
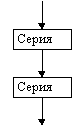
Структура “следование” |
|
|
|
|
|
На схемах СЕРИЯ обозначает один или несколько любых операторов; УСЛОВИЕ есть логическое выражение (ЛВ) (если его значение ИСТИНА, переход происходит по ветви ДА, иначе — по НЕТ). На схеме цикла с параметром использованы обозначения: ПЦ — параметр цикла, НЗ — начальное значение параметра цикла, КЗ — конечное значение параметра цикла, Ш — шаг изменения параметра цикла.
Линейные алгоритмы
Простейшие задачи имеют линейный алгоритм решения. Это означает, что он не содержит проверок условий и повторений.
Ветвление
Достаточно часто то или иное действие должно быть выполнено в зависимости от значения логического выражения, выступающего в качестве условия. В таких случаях используется развилка.
Циклы
Если какие-либо операторы необходимо выполнить несколько раз, то их не переписывают каждый раз заново, а организуют цикл.
Вопрос №20 Стандартные алгоритмы. Действия с целыми числами. Суммирование и умножение. Вычисление многочлена по схеме Горнера.
Алгоритм Евклида
В качестве примера алгоритма рассмотрим известный из школьной математики алгоритм Евклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел. Входными данными алгоритма являются два натуральных числа a и b, а выходными данными будет одно натуральное число — НОД чисел a и b.
Описание алгоритма:
Если a = b, то НОД = a = b и заканчиваем вычисления.
Если a > b, то из a вычитаем b (
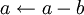 ).
Переходим к 1.
).
Переходим к 1.
Если же b > a, то из b вычитаем a (
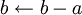 ).
Переходим к 1.
).
Переходим к 1.
Схема Горнера
Рассмотрим еще один важный пример функции на последовательности. Пусть дана последовательность коэффициентов многочлена p(x) по убыванию степеней:
p(x) = a0xn +a 1xn-1 + ... + an
Нужно вычислить значение многочлена в точке x = t. Алгоритм, основанный на просмотре последовательности коэффициентов в направлении от старшего к младшему, называется схемой Горнера. Проиллюстрируем его идею на примере многочлена третьей степени:
p(x) = ax3+bx2+cx+d
Его можно представить в виде
p(x) = ((ax+b)x+c)x+d
Для вычисления значения многочлена достаточно трех умножений и трех сложений. В общем случае, многочлен представляется в следующем виде:
p(x) = (...((a0x+a1)x+a2)x+...+an-1)x+an.
Обозначим через pk(x) многочлен k-ой степени, вычисленный по коэффициентам a0, a1, ..., ak:
pk(x) = a0xk + a1xk-1 + ... + ak.
Тогда
pk+1(x) = pk(x)x + ak+1
т.е. при считывании нового коэффициента многочлена надо старое значение многочлена умножить на значение x, а затем прибавить к нему новый коэффициент.
Выпишем алгоритм:
вещ алгоритм схема Горнера(вх: цел n, вещ a[n+1], вещ t)
| дано: n -- степень многочлена
| a[n+1] -- массив коэффициентов многочлена по
| убыванию степеней
| надо: вычислить значение многочлена в точке t
начало алгоритма
| вещ p; цел i;
| p := 0.0; // Инициализация значения многочлена
| i := 0;
| цикл пока i <= n
| | p := p * t + a[i]; // Вычисление нового значения по
| | // старому значению и добавленному коэффициенту
| | i := i + 1;
| конец цикла
| ответ := p;
конец алгоритма

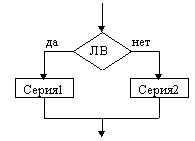 Полное
ветвление
Полное
ветвление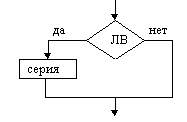 Неполное
ветвление
Неполное
ветвление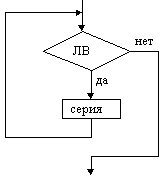 Цикл
с предусловие
(цикл ПОКА)
Цикл
с предусловие
(цикл ПОКА)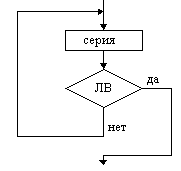 Цикл
с постусловием
(цикл ДО)
Цикл
с постусловием
(цикл ДО)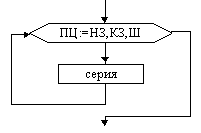 Цикл
с параметром
Цикл
с параметром