1.3.4 Основные понятия многократного измерения и алгоритмы обработки многократных измерений

 

На практике приходится довольствоваться ограниченным числом измерений для того, чтобы оценить «истинное» значение измеряемой величины и точность измерения.

Если число измерений велико (более 100), то кривую распределения можно построить достаточно точно, и если она соответствует нормальному закону, то графически определяется математическое ожидание m_x и среднее квадратическое отклонение σ. Результаты измерений х₁, х₂, …, х_n делят на 10…20 интервалов Δх и записывают в виде статистического ряда, где: m_i – число результатов в интервале; P_i – вычисленная вероятность попадания в данный интервал (доверительная вероятность):

 

	Δх1	Δх2	…	Δхn
mi	m1	m2		mn
Рi	Р1	Р2		Рn

 

При этом Σ m_i = n; P_i = m_i / n.

 

Статистический ряд служит основой для построения гистограммы и статистической функции распределения (рисунок 1.3.1). При Δх → 0 гистограмма переходит в плавную кривую (см.тему 7 Раздела I и практическую работу №1).

Соответствие полученной кривой закону нормального распределения проверяют по критериям Пирсона или Холмогорова.

Если измерений менее 15, то принадлежность экспериментального распределения к нормальному не проверяется.

При обработке результатов ограниченного числа наблюдений в качестве оценки математического ожидания принимается среднее арифметическое результатов наблюдений:

(1.3.8)

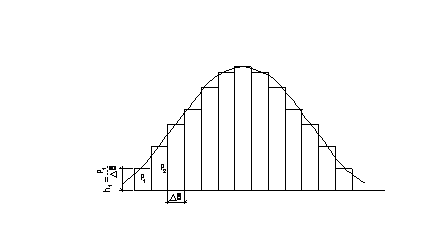
Рисунок 1.3.1 – Построение гистограммы и статистической функции распределения по опытным данным:s

Δх – принятый интервал;

Р₁, Р₂ – вероятность попадания соответственно в интервалы 1 и 2;

h₁ – ордината функции распределения в точке 1.

 

Приближенное значение среднего квадратического отклонения в этом случае вычисляется по формуле:

.

(1.3.9)

Появление в знаменателе выражения (n-1) вместо n связано с заменой математического ожидания средним арифметическим незначительного числа наблюдений.

Среднее арифметическое отличается от математического ожидания на величину случайной погрешности (погрешности среднего значения), которая подчиняется тому же закону распределения, что и погрешности результатов отдельных наблюдений.

Дисперсия среднего арифметического вычисляется по формуле:

,

(1.3.10)

      

а среднее квадратическое среднего арифметического – по формуле:

.

(1.3.11)

При увеличении числа наблюдений и   .

При числе наблюдений n>20 значения коэффициента t определяют по таблицам функции Лапласа, а при n<20 – по таблицам функции Стъюдента.

Зная число наблюдений n и задавшись доверительной вероятностью Р, можно найти значение t и, умножив его на , определить границы доверительного интервала.